Understanding Top-K Sparsification in Distributed Deep Learning

정지현·2023년 8월 7일

Federated Learning Gradient Sparsification

논문리뷰

목록 보기

2/2

distributed SGD가 large-scale deep learning model 학습에 많이 사용되고 있는데 communication overhead 문제가 있어서 이를 해결하기 위해 TopK-SGD이 등장했다.

training 동안 TopK-SGD의 gradient distribution을 자세히 보고 GPU의 효율적인 사용을 위해 이를 활용한 approximate top-k selection algorithm을 제안한다.

1. Introduction

P: number of workers
x: x $\in R^d$ , model parameters with d 차원

t번째 iteration에서 distributed synchronous SGD가 model parameter 를 update 하는 식은 다음과 같다.

x_{t+1} = x_t - \eta_t {1\over P} \sum_{p=1}^Pg_t^p

P 개의 workers 에서 모두 d차원의 gradients 를 받아서 합칠 때 communication complexity 가 O(d) 이므로 각 worker에서 k개씩 뽑기 위해서 Compressor $Com_k$ 가 각 worker에 적용된다. 0 으로 바꿔준 d-k개의 elements는 residual $\epsilon_t^p$ 으로 저장된다.

x_{t+1} = x_t - \eta_t{1\over P}Comp_k(g_t^p + \epsilon_t^p)

\epsilon_{t+1} = g_t^p + \epsilon_t^p - Comp_k(g_t^p + \epsilon_t^p)

이론적으로는 gradient sparsification 을 적용한 distributed SGD 가 vanilla SGD 와 convergence rate 이 비슷하다는 사실이 증명되었다 . convergence rate 은 $Comp_k$ 의 특징에 따라 결정된다.

$\mathbb{E_c}$ : expectation taking on the compressor

\mathbb{E_c} [\Vert x - Comp_k(x)\Vert^2] \leq (1-k/d)\Vert x\Vert^2 , \forall x \in \mathbb{R}_d

여기서 Comp_k 의 종류에 따라 Top_k 나 Rand_k 가 올 수 있는데, 다음 수식은 명백하게 참이다.

\Vert x - Top_k(x)\Vert^2 \leq \Vert x - Rand_k(x)\Vert^2 \\\ \mathbb{E_R} [\Vert x - Rand_k(x)\Vert^2] = (1-k/d)\Vert x\Vert^2

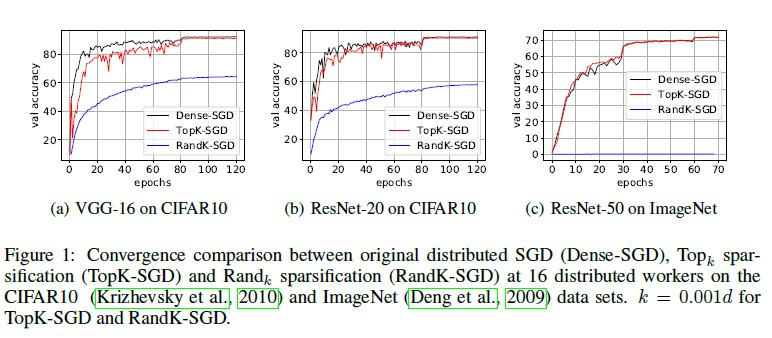
기존 연구에서 Rand_k 보다 Top_k에서 Convergence rate이 더 빠르다는 것은 실험적으로 증명이 되었지만 두 operator 사이의 convergence behavior 에서 차이점은 찾아내지 못했다.

본 논문에서는 TopK-SGD 가 기존의 Dense-SGD 와 비슷한 성능을 보인다는 것을 증명했고 distributed SGD에서 Topk operator 의 동작 디테일에 대해 보려고 한다.

Contributions

local stochastic gradients에 대한 디테일 관찰 → gradient의 좌표가 bell shaped distribution를 따름
bell shaped distribution 을 이용하여 어떻게 TopK가 RandK보다 뛰어난 성능을 보이는지 설명
design and implement approximate top-k selection algorithm.

3. Study On Stochastic Gradients

3.1 Gradient Distribution

update에 더 많은 영향을 주는 “significant” element를 고르는 것이 sparsification의 기본 규칙이다. 그렇다면 중요한 숫자와 랜덤하게 선택된 숫자들 에는 어떤 차이가 있을까?

실험 세팅

TopK-SGD 에서 k = 0.001d(for d 차원의 weights) 로 설정.

measure histograms of local gradients accumulated with the residuals. $u_t^p = g_t^p + \epsilon_t^p$
모델 마다 약간 다른 모양이지만 공통적으로 대부분의 값들이 0에 가까웠다.

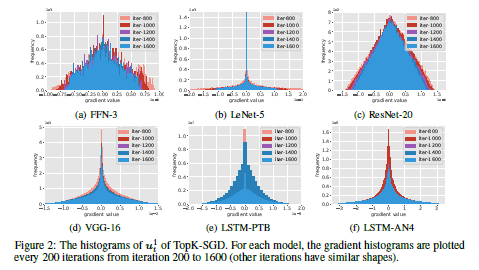
full gradient SGD 보다 더 넓은 종모양을 띈다. 왜지..?

가장 큰 k개의 값을 고를 때 histogram에서 왼쪽이나 오른쪽에 있는 값들을 골라야 한다.
그러므로 $u_t$ 에 대해 top_k를 수행할 때 Top_k(u_t) 롸 u_t가 얼마나 가까운지 비교하기 위해 다음 식 형태로 표현

\Vert Top_{k}(u_t)\Vert ^2 < \Vert u_t \Vert ^2

\Vert u_t - Top_k(u_t)\Vert ^2 \leq \gamma\Vert u_t\Vert ^2 \\ for \ \gamma \leq (1 - k/d)

3.3 GaussianK : An Approximate TopK Operator

Top_k 는 GPU 처럼 여러개의 코어로 이루어져서 병렬 연산이 가능한 환경에서는 비효율적이다.

key idea

d-dimension의 gradient를 정규분포로 봄 → GPU 친화적인 방식으로 O(d) 에 계산 가능하도록
u_t 의 percent point function 을 통해 threshold 를 추정
정확히 정규분포가 아니므로 실제 topK에 근사할 수 있도록 조정

4. Experiment

4.1 Experiment Settings

Numerical results of equation - 가우시안 분포에서 랜덤으로 고른 100,000 dim vector로 실험
Nvidia Tesla V100 GPU , k = 0.001d
End-to-end training speed ; 10 Gbps Ethernet GPU

gradient sparsification에 집중했기 때문에 fp32로 사용

🛠 CUDA-10.1, cuDNN-7.5.0, NCCL-2.3.7, PyTorch-1.1.0, OpenMPI-4.0.1, and Horovod-0.16.4 (Sergeev & Balso, 2018)

4.2 Numerical Results Of the TopK Operator

4.3 GPU Computation Efficiency Of Sparsification

d를 20M 부터 400M 까지 (k=0.001d로 설정) 모두 해봤는데 d 가 커질수록 Top_k는 엄청 느려지는 반면 GaussianK는 그렇게 까지 느려지지는 않음

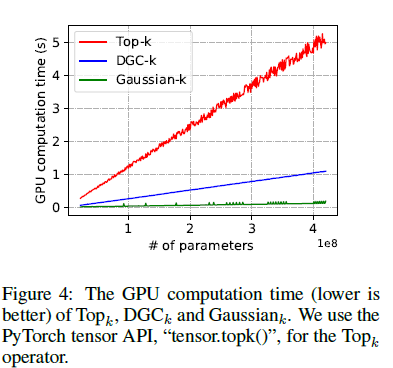
4.4 Convergence Performance of GaussianK-SGD

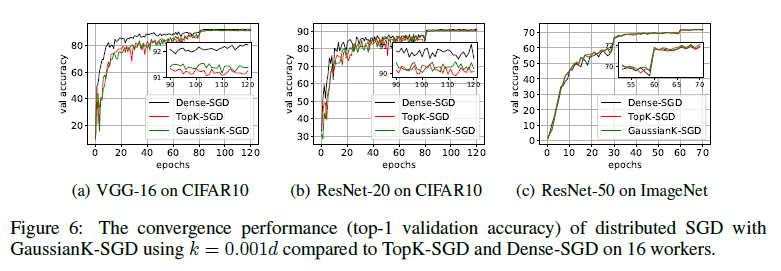
GaussianK-SGD 와 TopK-SGD 의 정확도가 Dense-SGD 보다 정확도가 조금 떨어지는데, 그 이유는 residual 이 원래 gradient에 비해 잘 업데이트 되지 않아서 그런 것으로 추정된다.
momentum correction같은 optimization기법을 이용하여 이 문제를 해결할 수 있을 것이다.