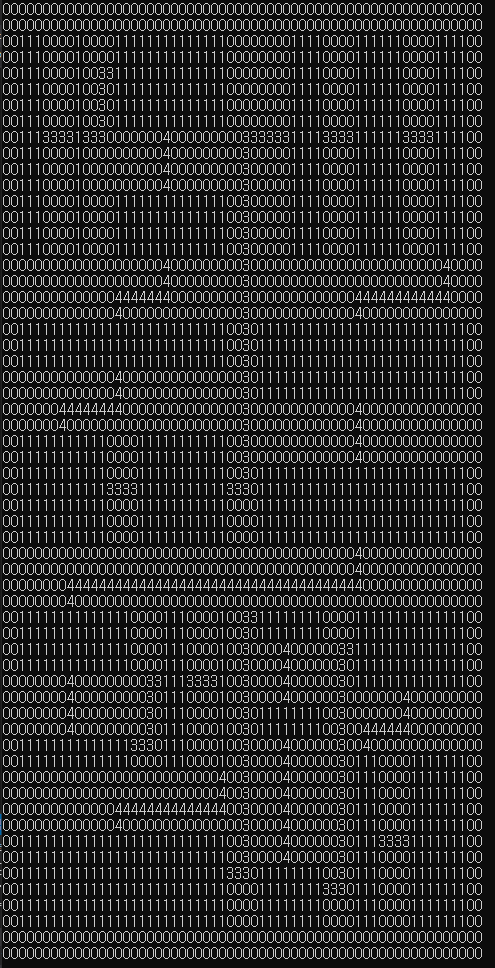
개요

• BSP(Binary Space Partitioning, 이진 공간 분할법)이란 재귀적으로 유클리드 공간을 초평면 상의 볼록 집합으로 분할하는 기법이다. 분할 과정으로 BSP 트리라 불리는 트리 구조가 만들어진다.

• 3차원(또는 2차원) 공간을 효율적으로 다루기 위해, 하나의 공간을 재귀적으로 둘씩 나누어가는 기법이라는 뜻이다.

• 3D 게임 엔진에서 맵을 렌더링할 때, 충돌 감지를 수행할 때, 레이트레이싱을 할 때 등 다양한 분야에서 연산을 최적화하려고 할 때 자주 사용된다.

• 이번에는 로그라이크류 게임에서 맵을 랜덤으로 나눌 때 어떻게 사용할 수 있는지 정리해보고자 한다.

알고리즘의 흐름

1. 분할할 공간(씬, 맵, 월드 등)을 하나 정한다.

2. 하나의 분할 평면(또는 분할선)을 선택하여 현재 공간을 두 개의 하위 공간으로 나눈다.

3. 각 하위 공간에 대해 같은 과정을 재귀적으로 반복한다.

4. 원하는 기준(최종 목적)에 도달할 때까지 이 과정을 수행한다.

• 이 과정을 거쳐 만들어진 트리를 BSP 트리라고 부른다.

• 트리의 각 노드는 분할을 위한 평면(또는 선)에 대한 정보를, 리프(leaf) 노드는 최종적으로 분할이 완료된 공간 정보를 담게 된다.

BSP 트리 만들기

• BSP 트리를 사용하여 페인터 알고리즘을 사용해 다각형을 렌더링할 수 있다. 다각형 목록에서 BSP 트리를 구성하는 재귀 알고리즘은 다음과 같다.

1. 목록에서 다각형(Polygon) P를 하나 선택한다.

2. BSP 트리에 노드 N을 만들고, P를 해당 노드의 다각형 목록에 추가한다.

3. 목록에 있는 다른 모든 다각형에 대해 다음을 수행한다.

   1. 해당 다각형이 P를 포함하는 평면의 '앞(front)'에 완전히 놓여 있다면, 그 다각형을 P 앞쪽 노드의 다각형 목록으로 옮긴다.

   2. 해당 다각형이 P를 포함하는 평면의 '뒤(behind)'에 완전히 놓여 있다면, 그 다각형을 P 뒤쪽 노드의 다각형 목록으로 옮긴다.

   3. 해당 다각형이 P를 포함하는 평면과 교차한다면, 두 개의 다각형으로 나누어 앞·뒤 노드 각각에 옮긴다.

   4. 해당 다각형이 P를 포함하는 평면 위에 놓여 있다면, 그 다각형을 노드 N의 다각형 목록에 추가한다.

4. P 앞쪽에 있는 다각형 목록에 대해 위 알고리즘을 재귀적으로 적용한다.

5. P 뒤쪽에 있는 다각형 목록에 대해서도 같은 알고리즘을 재귀적으로 적용한다.

예시

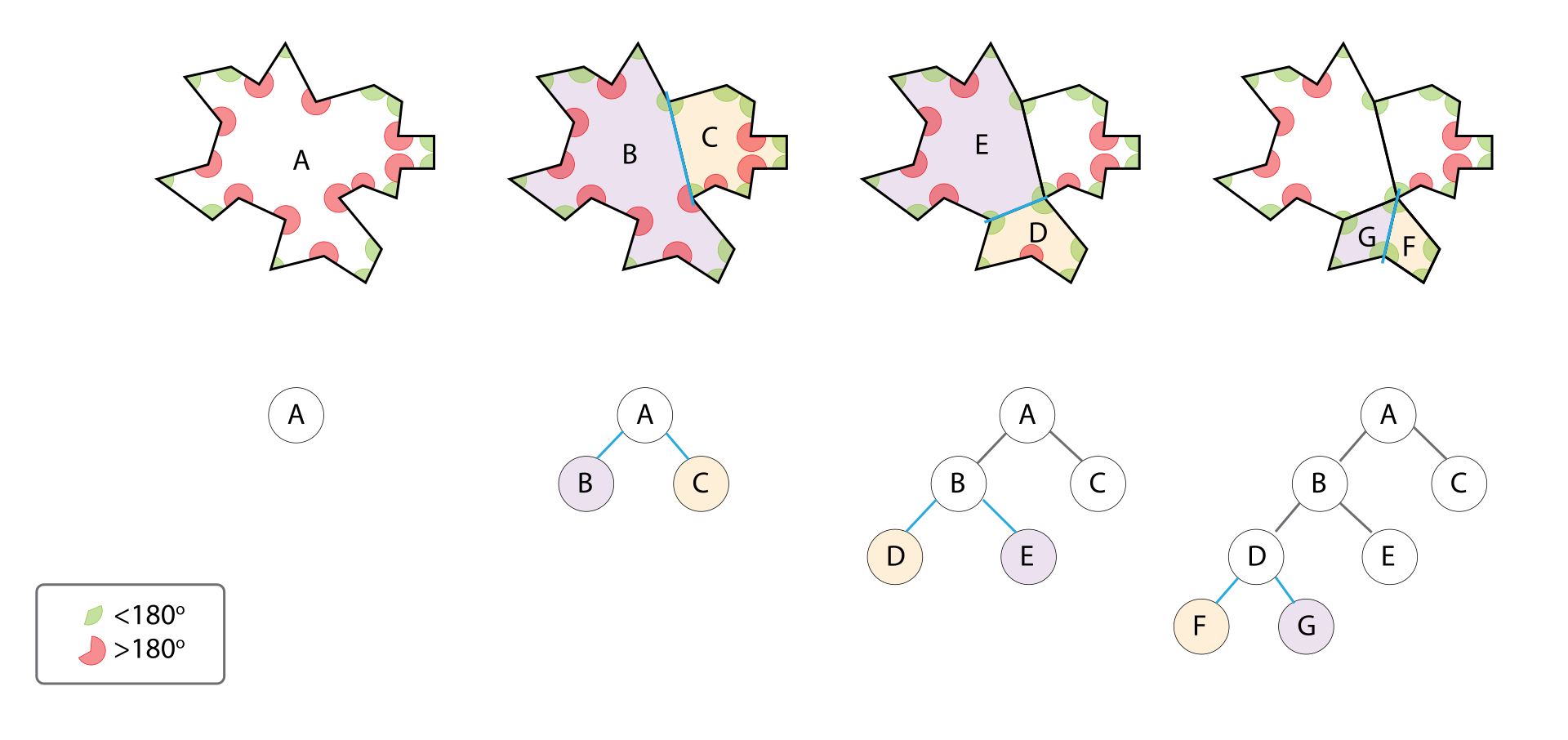
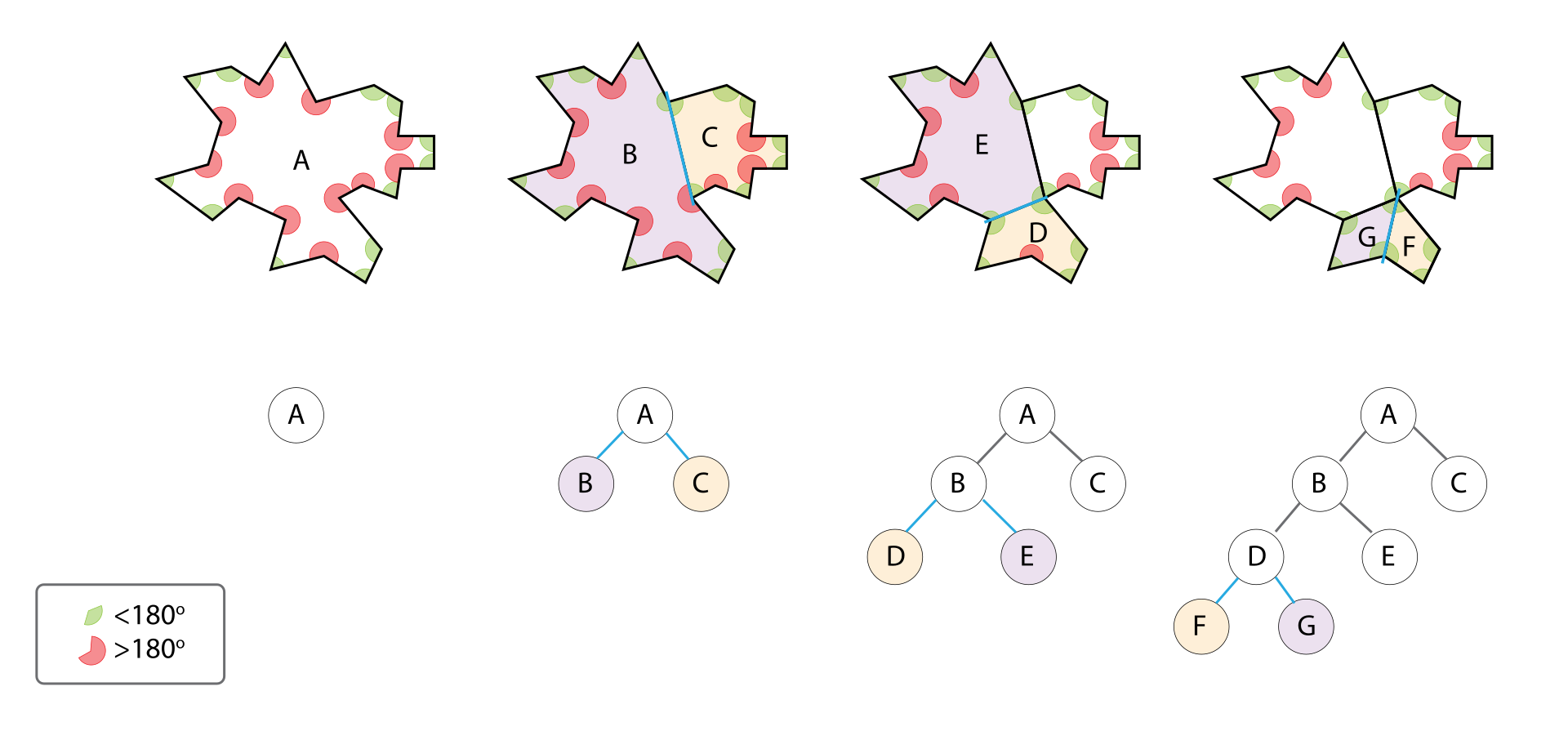
• 아래 다이어그램은 위 알고리즘을 사용하여 선분(또는 다각형) 목록을 BSP 트리로 변환하는 과정을 예시로 보여준다. 8단계 각각에서 위 알고리즘이 선분 목록에 적용되어 트리에 새 노드가 추가된다.

• 먼저 장면(Scene)을 구성하는 선분(2D) 혹은 다각형(3D) 목록을 가지고 시작한다. 트리 도식에서, ‘목록(list)’은 둥근 사각형으로, BSP 트리의 노드는 원으로 표시한다. 공간 상에서 선분의 ‘앞(front)’ 방향은 화살표로 표시되어 있다.

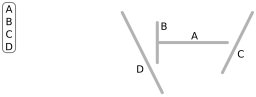
1. 위 알고리즘의 단계를 따르면,

   1. 목록에서 선분 A를 하나 선택하고,

   2. 이를 노드에 추가한다.

   3. 목록에 남아 있는 다른 선분들을 A가 놓인 평면(여기서는 2D이므로 직선)의 앞쪽에 있는 것(B2, C2, D2)과 뒤쪽에 있는 것(B1, C1, D1)으로 분할한다.

   4. 먼저 A 앞쪽에 있는 선분들(B2, C2, D2)을 처리한다(단계 2 ~ 5).

   5. 그리고 나서 A 뒤쪽에 있는 선분들(B1, C1, D1)을 처리한다(단계 6 ~ 8).

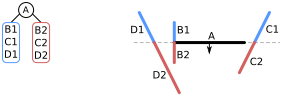
2. 이번에는 A 앞쪽에 있는 선분 목록(B2, C2, D2)에 알고리즘을 적용한다. 선분 B2를 선택하여 노드에 추가하고, 남은 선분들을 B2의 앞쪽에 있는 선분(D2)과 뒤쪽에 있는 선분(C2, D3)으로 분할한다.

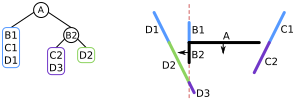
3. B2 및 A의 앞쪽 목록에 있는 선분들 중 D2를 선택한다. 이 목록에는 오직 D2만 존재하므로, 노드에 D2를 추가한 뒤에는 추가로 할 작업이 없다.

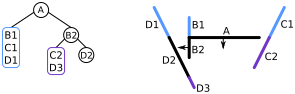
4. 이제 B2 앞쪽의 선분 처리를 마쳤으므로, B2 뒤쪽에 있는 선분(C2, D3)을 살펴본다. 이 중에서 C2를 하나 선택하여 노드에 추가하고, 남은 선분(D3)을 C2의 앞쪽 목록에 추가한다.

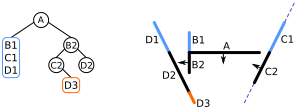
5. C2 앞쪽 목록에 있는 선분을 확인한다. 유일한 선분은 D3이므로 이를 노드에 추가하고 계속 진행한다.

6. 이제 A 앞쪽에 있었던 모든 선분을 BSP 트리에 추가했으므로, 이번에는 A 뒤쪽에 있는 선분 목록을 처리한다. 해당 목록에서 하나의 선분(B1)을 고르고 노드에 추가한 후, 나머지 선분들을 B1의 앞쪽(즉, D1)과 뒤쪽(즉, C1)으로 분할한다.

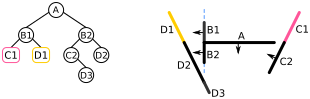
7. 먼저 B1 앞쪽에 있는 선분 목록을 처리한다. 여기에는 D1만 있으므로, 이를 노드에 추가하고 계속 진행한다.

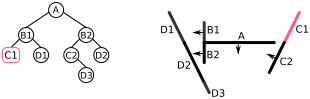
8. 다음으로 B1 뒤쪽에 있는 선분 목록에는 C1만 있으므로, 이를 노드에 추가하고 BSP 트리 구성을 마친다.

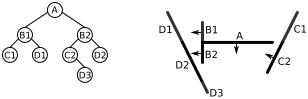
• BSP 트리에 포함되는 다각형(혹은 선분)의 최종 개수는 원래 목록보다 많아질 때가 많다. 이는 분할 평면을 가로지르는 다각형(혹은 선분)이 두 개로 나누어지기 때문이다. 이 증가를 최소화하는 것이 바람직하지만, 최종 트리가 적절한 균형을 유지하도록 하는 것도 중요하다. 따라서 효율적인 BSP 트리를 생성하려면 분할 평면(알고리즘의 1단계)으로 사용되는 다각형(혹은 선분)을 선택하는 것이 중요하다.

최종 목적

• BSP 알고리즘에서 최종 목적이란 언제까지 분할을 계속할 것인가?이다.

• 이 최종 목적은 렌더링 최적화, 충돌 검출, 레이 트레이싱, 조명(라이팅) 계산, 렌더링 파이프라인의 클리핑, 그리고 레벨 디자인(게임 맵 생성) 등이 될 수 있다.

1. 렌더링 최적화(Visibility Determination)

• 예) 3D 게임 엔진에서 시야에 보이는 부분만 효율적으로 그리기 위해 공간을 분할하고, 가시성을 판단하는 용도.
• 최종 목적: 각 리프 노드가 너무 작게 잘게 분할되기 전에(적정 크기 이하로) 멈추거나, 혹은 조망(시야) 계산이 더 이상 필요 없는 수준으로 쪼개졌을 때 멈춤.

2. 충돌 검출(Collision Detection)

• 예) 물리 엔진에서 객체 충돌을 빠르게 판단하기 위해 공간을 분할.
• 최종 목적: 분할된 리프 공간 내부에 포함된 오브젝트 수가 일정 기준 이하가 되면 더 이상 분할하지 않음. (예: 리프 노드에 객체가 1~2개만 남거나, 리프 공간의 크기가 임계점보다 작아졌을 때)

3. 레이 트레이싱(Ray Tracing)

• 광선을 쏠 때 충돌할 가능성이 있는 폴리곤/오브젝트만 빠르게 찾기 위해 BSP 트리를 사용할 수 있음.
• 최종 목적: 광선 검출에 필요한 정확도를 만족할 만큼의 분할(즉, 충분히 세밀하게 오브젝트가 구분된 상태)이 이루어지면 더 이상 분할하지 않음.

4. 레벨 디자인(게임 맵 생성)

• 예) 2D/3D 게임에서 랜덤 던전, 방, 복도 구조 등을 만들기 위해 공간을 재귀적으로 분할.
• 최종 목적: “방(룸)” 크기나 개수, 또는 연결 경로(복도)의 수가 원하는 수준에 도달할 때까지 분할. 이후 각 리프 노드를 방이나 복도로 활용.

5. 조명(라이팅) 계산

• 예) 라이트맵(Lightmap)을 생성하기 위해서, 또는 GI(Global Illumination)을 계산하기 위해 공간을 분할.
• 최종 목적: 광원과 표면 간의 상호작용을 계산하기에 충분히 세밀한 분할 상태에 도달하면 더 이상 쪼개지 않음.

6. 클리핑(Clipping)이나 페인터 알고리즘에 활용

• 예) 고전 렌더링 파이프라인에서 배경(뒤에 있는 오브젝트)를 먼저 그리거나, 앞의 물체에 가려지는 뒷부분은 그리지 않도록 공간 분할.
• 최종 목적: 오브젝트 간 가려짐(Visibility)을 판별하기에 충분할 정도로 나누면 멈춤.

분할 종료 조건

• 최종 목적에 따라 분할 종료 조건은 아래와 같이 정할 수 있다.

1. 오브젝트 개수 기준 : 분할된 공간(리프 노드) 안에 들어 있는 오브젝트(폴리곤 등) 수가 특정 개수 이하가 되면 더 이상 분할하지 않는다.

2. 공간 크기(깊이) 기준 : 분할된 공간의 부피(또는 면적)가 일정 이하로 작아지면 중단한다.

3. 계산 비용과 효율의 기준 : 더 이상 분할을 해봤자 얻을 수 있는 최적화 이점이 작거나, 오히려 분할 관리 비용이 커지면 중단한다.

4. 사용자가 설정한 임의의 기준: 예를 들어 게임 레벨 디자인에서 “방은 최소 3m x 3m 크기, 최대 10개” 같은 조건을 미리 설정해두고, 그 조건을 만족하면 중단한다.

• 이처럼 BSP 알고리즘의 최종 목적에 따라 맞는 분할 종료 조건을 미리 정해 둔 후, 그 조건에 도달할 때까지 공간을 재귀적으로 이등분하는 과정이다.

구현

레벨 디자인 - 텍스트 게임

• 로그라이크 게임의 경우, 매번 새로운 맵을 생성하기도 한다. 그 때 BSP 알고리즘을 응용할 수 있다. 이번에는 cpp로 텍스트로 이루어진 맵을 만들 것이다.
  • 분할 정복을 하고 방을 이어붙이는 BSP 알고리즘을 간단히 만든 예시이다. 엄밀하게는 조금 다르지만, 이진 방식으로 공간을 나눈다는 점에서 비슷하다고 볼 수 있다. 흔히 BSP 던전 생성 알고리즘이라고 하는 기법이다.

1. 공간을 둘로 분할한다. 분할 종료 조건을 정하고 실행한다.

   • 이번에는 랜덤으로 가로로 할지 세로로 할지, 분할 비율을 어디에 더 크게 할지를 정한다. 너무 한쪽으로만 분할되지 않도록 조건을 추가하였다.

     if (rLen / cLen > 1 || (cLen / rLen <= 1 && rand() % 2))
     {
     	int divideNum = (r2 - r1) * (rand() % 3 + 4) / 10; // 랜덤비율설정
     	...
     }

2. 분할이 끝나면 방을 만든다.

   • 분할된 공간은 1을 넣어 방으로 표시한다. 후에 길을 추가하기 위해 전체 직사각형 각 변에서 2씩 빼어 공간을 나눈다.

     if (depth == 0 || (r2 - r1 <= 10 || c2 - c1 <= 10))
     {
     	for (int i = r1 + 2; i < r2 - 2; ++i)
        {
     		for (int j = c1 + 2; j < c2 - 2; ++j)
            {
     			Dungeon[i][j] = 1;
     		}
     	}
     	return {r1 + 2, c1 + 2, r2 - 3, c2 - 3, r1 + 2, c1 + 2, r2 - 3, c2 - 3 };
     }

3. 분할된 방 사이에 길을 만든다.

   • 재귀를 통해 방을 연결한다.

     ...
     Dungeon[temp1.r4 + 1][(temp1.c3 + temp1.c4) / 2] = 4;
     Dungeon[temp1.r4 + 2][(temp1.c3 + temp1.c4) / 2] = 4;
     Dungeon[temp2.r1 - 1][(temp2.c1 + temp2.c2) / 2] = 4;
     Dungeon[temp2.r1 - 2][(temp2.c1 + temp2.c2) / 2] = 4;
     int rmin = min((temp1.c3 + temp1.c4) / 2,(temp2.c1 + temp2.c2) / 2);
     int rmax = max((temp1.c3 + temp1.c4) / 2, (temp2.c1 + temp2.c2) / 2);
     for (int i = rmin; i <= rmax; ++i)
     {
     	Dungeon[temp2.r1 - 2][i] = 4;
     }
         ...

4. 전체 코드와 결과

   #include<stdio.h>
   #include<iostream>
   #include<algorithm>
   #include<string>
   #include<string.h>
   #include<math.h>
   using namespace std;
   
   #define DungeonSize 60
   int dungeon[DungeonSize][DungeonSize];
   
   //1.분할한다.
   //2. 분할이 끝나면 방을 만든다.
   //3. 방을 연결한다.
   typedef struct DungeonLocation
   {
   	int r1, c1, r2, c2;
   	int r3, c3, r4, c4;
   };
   
   DungeonLocation DivideDungeon(int depth, int r1, int c1, int r2, int c2)
   {
   	DungeonLocation location;
   	//2. 방을 만든다. 
   	if (depth ==0 || (r2 - r1 <= 10 || c2 - c1 <= 10)) 
      {
   		for (int i = r1 + 2; i < r2 - 2; ++i) 
          {
   			for (int j = c1 + 2; j < c2 - 2; ++j) 
              {
   				dungeon[i][j] = 1;
   			}
   		}
   		
   		return { r1 + 2, c1 + 2, r2 - 3, c2 - 3, r1 + 2, c1 + 2, r2 - 3, c2 - 3 };
   	}
   
   	//1. 분할한다
   	//3. 방을 합친다.
   	int rLen = r2 - r1;
   	int cLen = c2 - c1;
   	DungeonLocation temp1, temp2;
   	if (rLen/cLen > 1 ||(cLen/rLen <= 1 && rand() % 2))
      { // 세로분할
   		int divideNum = (r2 - r1) * (rand() % 3 + 4) / 10;
   		//방 분할
   		temp1 = DivideDungeon(depth - 1, r1, c1, r1 + divideNum, c2);
   		temp2 = DivideDungeon(depth - 1, r1 + divideNum, c1, r2, c2);
   		
   		//방합치기.
   		dungeon[temp1.r4 + 1][(temp1.c3 + temp1.c4) / 2] = 4;
   		dungeon[temp1.r4 + 2][(temp1.c3 + temp1.c4) / 2] = 4;
   		dungeon[temp2.r1 - 1][(temp2.c1 + temp2.c2) / 2] = 4;
   		dungeon[temp2.r1 - 2][(temp2.c1 + temp2.c2) / 2] = 4;
   		int rmin = min((temp1.c3 + temp1.c4) / 2,(temp2.c1 + temp2.c2) / 2);
   		int rmax = max((temp1.c3 + temp1.c4) / 2, (temp2.c1 + temp2.c2) / 2);
   		for (int i = rmin; i <= rmax; ++i) 
          {
   			dungeon[temp2.r1 - 2][i] = 4;
   		}
   	}
   	else 
      {// 가로분할
   		int divideNum = (c2 - c1) * (rand() % 3 + 4) / 10;
   		//방분할
   		temp1 = DivideDungeon(depth - 1, r1, c1, r2, c1 + divideNum);
   		temp2 = DivideDungeon(depth - 1, r1, c1 + divideNum, r2, c2);
   		
   		//방합치기
   		dungeon[(temp1.r3 + temp1.r4) / 2][temp1.c4 + 1] = 3;
   		dungeon[(temp1.r3 + temp1.r4) / 2][temp1.c4 + 2] = 3;
   		dungeon[(temp2.r1 + temp2.r2) / 2][temp2.c1 - 1] = 3;
   		dungeon[(temp2.r1 + temp2.r2) / 2][temp2.c1 - 2] = 3;
   
   		int rmin = min((temp1.r3 + temp1.r4) / 2, (temp2.r1 + temp2.r2) / 2);
   		int rmax = max((temp1.r3 + temp1.r4) / 2, (temp2.r1 + temp2.r2) / 2);
   		for (int i = rmin; i <= rmax; i++) {
   			dungeon[i][temp2.c1-2] = 3;
   		}
   	}
   	location.r1 = temp1.r1;
      location.r2 = temp1.r2;
   	location.r3 = temp2.r3;
      location.r4 = temp2.r4;
      location.c1 = temp1.c1;
      location.c2 = temp1.c2;
      location.c3 = temp2.c3;
      location.c4 = temp2.c4;
   
   	return location;
   }
   
   void CreateDungeon() 
   {
   	memset(dungeon, 0, sizeof(dungeon));
   	DivideDungeon(5, 0, 0, DungeonSize, DungeonSize);
   }
   
   void PrintDungeon() 
   {
   	for (int i = 0; i < DungeonSize; ++i) 
      {
   		for (int j = 0; j < DungeonSize; ++j) 
          {
   			printf("%d", dungeon[i][j]);
   		}
   		printf("\n");
   	}
   }
   
   int main(void) 
   {
   	CreateDungeon();
   	PrintDungeon();
   }
   [출처] BSP(Binary Space Partitioning)알고리즘을 응용해 로그라이크류 게임 방만들기|작성자 jh20s

   

• C#과 유니티로도 이런 식으로 맵을 만들 수 있다. 이또한 BSP 알고리즘을 적용한 예시이다. 이 페이지 참고 / 이 페이지도 참고

참고

• BSP(Binary Space Partitioning)알고리즘을 응용해 로그라이크류 게임 방만들기
• 이진 공간 분할법 | Wikipedia
• Binary space partitioning | Wikipedia
• Binary Space Partitioning (BSP)란?
• [유니티] BSP 알고리즘을 이용해서 랜덤한 게임 맵 생성하기 [이론]
• 화가 알고리즘 | Wikipedia
• [유니티] 절차적 생성을 위한 던전 생성 알고리즘