백준 / 골드 5 / 1074. Z
- Z 모양 순서로 배열을 방문할 때,
(x, y)가 몇 번째로 방문되는지를 찾는 문제
- 재귀 문제라는 걸 파악하는 건 어렵지 않음
- 실제로 문제에
재귀적으로 순서대로 방문한다라고 대놓고 써져 있음
- 하지만 막상 재귀함수를 만들려고 하면, 대체 뭘 반환해야 할지 감이 안 잡힐 수 있음
풀이
def z_search(N, x, y):
if N == 1:
return 2*x + y
side = 2 ** N
half = side // 2
area = half ** 2
if 0 <= x < half:
if 0 <= y < half:
return z_search(N - 1, x, y)
else:
return area + z_search(N - 1, x, y - half)
else:
if 0 <= y < half:
return area * 2 + z_search(N - 1, x - half, y)
else:
return area * 3 + z_search(N - 1, x - half, y - half)
N, x, y = map(int, input().split())
print(z_search(N, x, y))
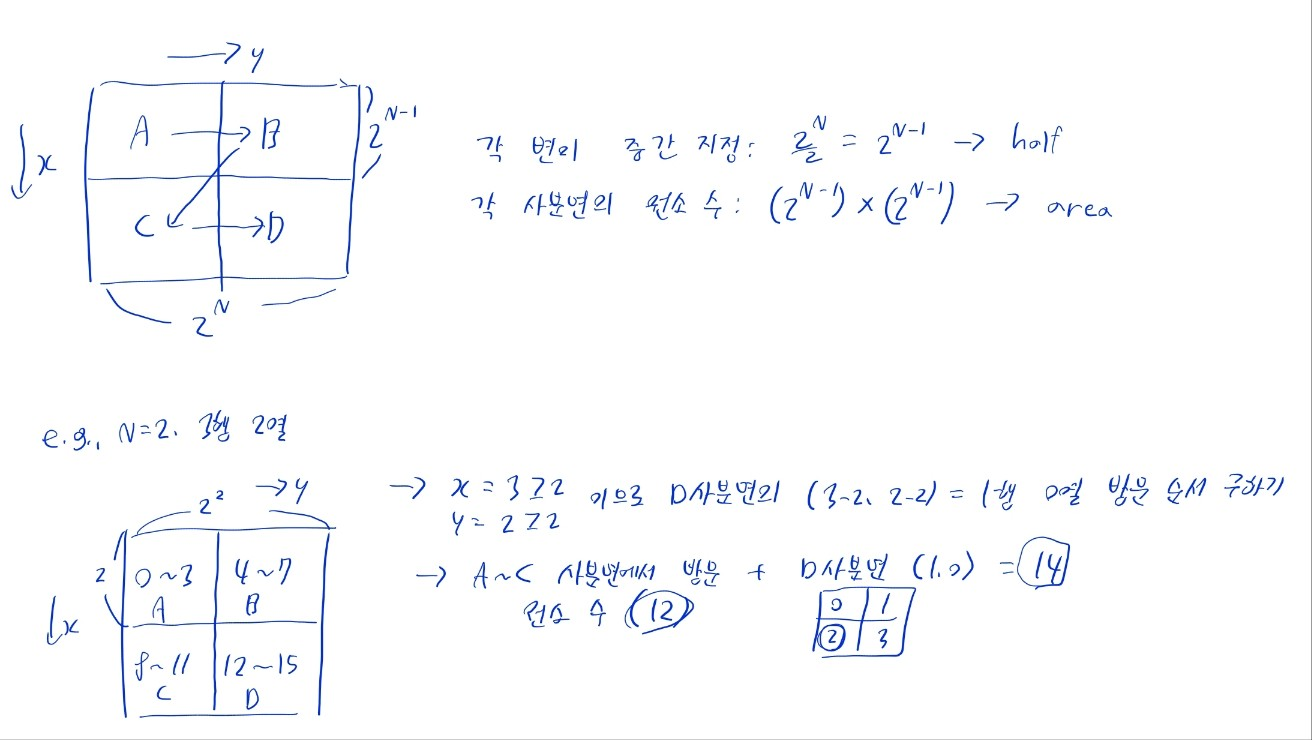
- 변의 길이(2N ->
side), 변의 길이의 절반(side // 2 -> half), 한 사분면의 원소 수 (half ** 2 -> area) 등을 변수로 만들어 두는 것이 편리함
- 크기가 2N×2N인 배열에서,
x행 y열의 방문 순서를 반환하는 함수 z_search 정의
- 이때 배열은
half × half 크기인 4개의 사분면으로 나뉘어짐
x행 y열이 어느 사분면에 속하는지 확인하고, 사분면 내 좌표로 재귀 호출- 특히
x >= half 혹은 y >= half 인 경우, 사분면 내 좌표를 구할 때 half만큼 빼 주어야 함
- 탐색은 좌상(A) -> 우상(B) -> 좌하(C) -> 우하(D) 사분면 순으로 이루어짐
- 이미 다른 사분면을 거친 경우, 이떼 방문한 원소의 수를 재귀함수의 결과에 더해서 반환
- 사분면마다
area개의 원소 수가 있으므로, 그만큼 더하면 됨
| 사분면 | 조건 | 이전 사분면에서 방문한 원소 수 |
|---|
| 좌상 (A) | x < half, y < half | 0 |
| 우상 (B) | x < half, y >= half | A 사분면에서 1 * area |
| 좌하 (C) | x >= half, y < half | A,B 사분면에서 2 * area |
| 우하 (D) | x >= half, y >= half | A,B,C 사분면에서 3 * area |
시간 복잡도
- 최대 N회 재귀 함수가 호출되므로 O(N)
기억할 점
- 변의 길이 등 자주 쓰일 것 같은 값은 무조건 변수로 저장한다. 코테에서 변수 많이 만든다고 손해볼 거 없다.

