[정글] 특히 어려웠던 녀석들
1.[백준] 1074. Z

변의 길이 등 자주 쓰일 것 같은 값은 무조건 변수로 저장한다. 코테에서 변수 많이 만든다고 손해볼 거 없다.
2.[백준] 2869. 달팽이는 올라가고 싶다

달팽이는 해롭다.
3.[백준] 9020. 골드바흐의 추측

에라토스테네스의 체를 다루는 문제다. 발음이 어려운데 에라-토스-테네스 처럼 끊어 말하면 쉽다.
4.[백준] 2628. 종이자르기

문제에 '가로', '세로', '행', '열', '격자' 등 표현이 보이는 순간, 종이에 그림부터 그리자. 머릿속에 떠올리며 풀려고 시도하다간 도중에 100% 헤맨다.
5.[백준] 10971. 외판원 순회 2

N이 턱없이 작으면 걱정 말고 경우의 수를 전부 확인해 보자. 어차피 고생은 너가 아니라 컴퓨터가 한다.
6.[백준] 2468. 안전 영역

2차원 배열에서 장애물 사이의 빈 공간의 수를 구하는 유형의 문제는 꽤나 자주 출제된다.
7.[백준] 1182. 부분수열의 합

순열 / 조합 문제를 재귀로 풀 땐, 직접 트리를 그려 스스로 생각한 논리가 맞는지 판단하고 코드를 친다.
8.[백준] 2805. 나무 자르기

탐색해야 하는 범위가 기상천외하게 넓은 경우, 이진 탐색 문제로 바꿔서 생각해 보자.
9.[백준] 2493. 탑

가장 최근에 조회, 저장한 데이터부터 확인할 방법이 필요하다? 스택을 떠올리자.
10.[백준] 2110. 공유기 설치

상록아, 발상을 역전시키는 거야!
11.[백준] 3190. 뱀

데이터의 입출력이 앞뒤에서 발생하는 경우, 큐를 떠올린다.
12.[백준] 1655. 가운데를 말해요

최대 힙, 최소 힙을 둘 다 활용하면 최솟값, 최댓값 아닌 수도 꺼내올 수 있다. 단지 그 방법을 떠올리는 건 너의 몫 ^^
13.[백준] 8983. 사냥꾼

이분 탐색은 빠르다. 한 문제에서 여러 번 이분 탐색을 사용하는 것에 부담을 갖지 말자.
14.[백준] 6549. 히스토그램에서 가장 큰 직사각형
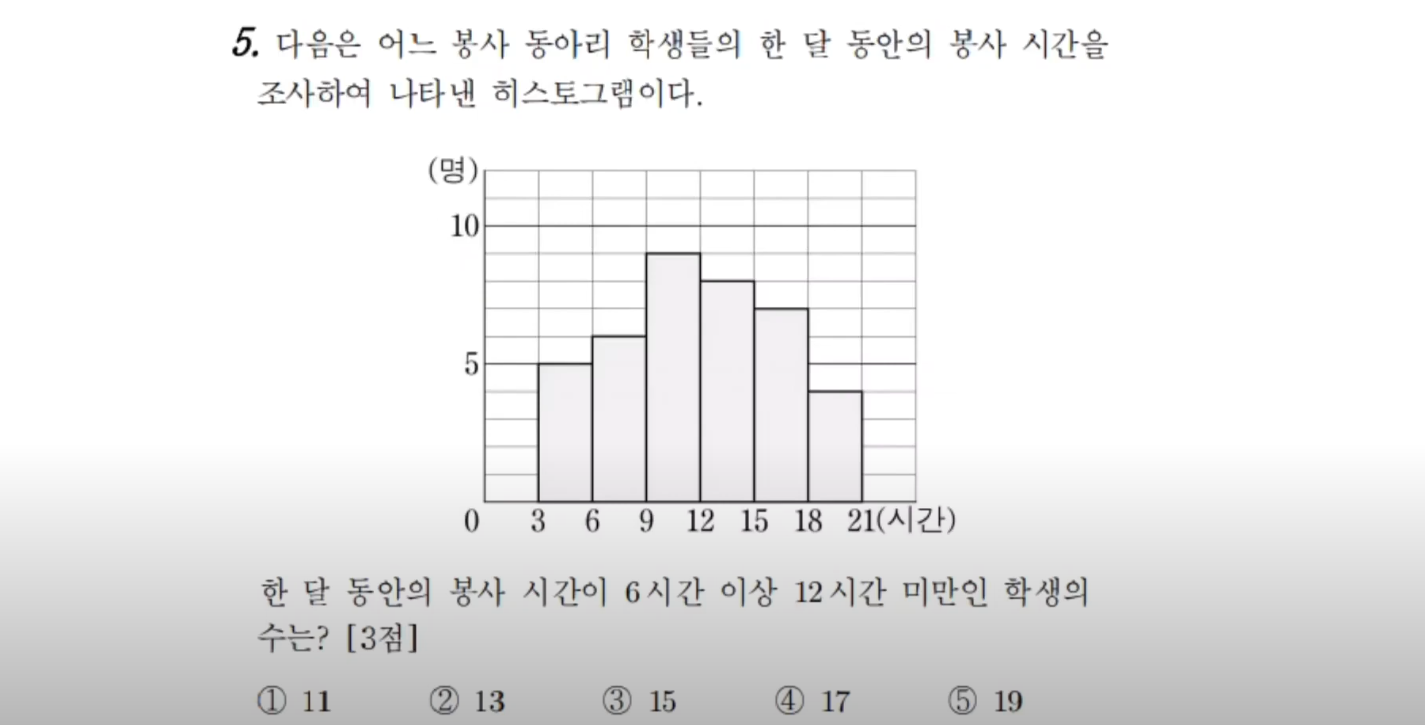
위 문제처럼 두 개의 인덱스 변수를 이동시켜 범위를 탐색하는 방법을 "투 포인터"라고도 부른다.
15.[백준] 13334. 철로

이 문제처럼 위치를 이동하면서 구간 내 생기는 변화를 파악하는 알고리즘 문제를 슬라이딩 윈도우라고도 부른다.
16.[백준] 11053 & 12015. 가장 긴 증가하는 부분 수열

빡센 이진탐색 문제 푸니까 힐링이 필요할 것 같아서 귀여운 사모예드 사진을 올렸습니다.
17.[백준] 10830. 행렬 제곱

분할 정복에선 무조건 무조건 무조건 중복되는 계산을 최소화해야 한다.
18.[백준] 1707. 이분 그래프

복잡한 조건을 만족해야 하는 문제에서는 일단 조건에 맞게 구성한 뒤, 진행 과정에서 모순이 발생하면 조건을 만족할 수 없는 것으로 판단한다.
19.[백준] 2665. 미로만들기

통과하게 되는 장애물의 수를 구하는 문제는, 0과 1의 가중치만을 가진 간선으로 이루어진 그래프에서 다익스트라 알고리즘을 수행하는 문제로 바꿔 풀 수 있다.
20.[백준] 2637. 장난감 조립

딕셔너리 관리가 복잡한 문제가 있다...? defaultdict를 써라.
21.[백준] 2573. 빙산

빡구현 문제는 끈기가 필요하다.
22.[백준] 2294. 동전 2

제일 '적은' '빠른' '가까운' '최소' 경우를 찾는 문제는 BFS로 빠르게 풀 수 있을 지도 모른다.
23.[백준] 2617. 구슬 찾기

모든 요소 / 성분 / 대상 사이 관계를 한 번에 알고 싶을 땐 플로이드 워셜을 사용한다. 다만 시간 복잡도가 높으니까, 사용하기 전에 문제의 크기는 반드시 고려한다.
24.[백준] 3055. 탈출

고슴도치는 귀엽다.
25.[백준] 14888. 연산자 끼워넣기

가능한 모든 경우의 수를 탐색할 때 DFS는 요긴하게 쓸 수 있다.
26.[백준] 9251. LCS (최장 공통부분 수열)

DP 문제인데 점화식을 떠올리기가 쉽지 않다...
27.[백준] 12865. 평범한 배낭

흔히 0-1 배낭 문제라고도 불립니다. 농담곰은 귀엽지만 이 문제는 절대로 안 귀엽습니다...
28.[백준] 9084. 동전

소신발언 하자면 전 알고리즘 중에서 DP가 제일 힘든 것 같습니다.
29.[백준] 1931. 회의실 배정

탐욕법엔 정렬이 많이 쓰인다. 매 순간 제일 작은/큰 값을 고르는 것도 탐욕적 선택이기 때문이다.
30.[백준] 11049. 행렬 곱셈 순서

행렬 너무 어렵습니다. 정석으로 복습하고 오겠습니다.
31.[백준] 2253. 점프

현재 상태를 노드로, 상태의 변화를 간선으로, 최소/최단의 정답 조건을 최단 거리로 생각하면, 전혀 다른 유형의 문제도 BFS로 바꿔 풀 수 있다.
32.[백준] 1700. 멀티탭 스케줄링

이중 반복문을 두려워하지 말자! 문제의 크기가 작으면 해볼 법하다.
33.[프머] 안전지대 / 성격 유형 검사하기 / 영어 끝말잇기

프로그래머스 "안전지대", "성격 유형 검사하기", "영어 끝말잇기" 세 문제를 풀어보았습니다.
34.[백준] 진우의 달 여행 / 음식물 피하기 / 빗물

백준 "진우의 달 여행", "음식물 피하기", "빗물" 문제를 풀어보았습니다.
35.[프머] 게임맵 최단거리 / 체육복 / 최빈값 구하기
프로그래머스 게임맵 최단거리, 체육복, 최빈값 구하기 문제를 풀어보았습니다.