백준 / 실버 1 / 10971. 외판원 순회 2
- 문제에서 N개의 도시를 모두 거쳐, 경로는 여러 가지가 있을 수 있는데... 같은 표현이 보인다.
- 왠지 순열의 냄새가 난다. 그것도 팩토리얼!!
- 그런데 2≤N≤10으로 값이 작다 보니, 완전 탐색(브루트포스)로 풀 수 있을 것 같다.
- 좋았어! 가능한 모든 경우의 수를 구해보자!!
시작 도시 고정하기
- 도시
0 ~ 3이 있을 때, 외판원이 0 -> 1 -> 2 -> 3 -> 0 순으로 돌았다고 가정하자
- 문제 설명에선 도시 번호를
1~N으로 두었지만, 문제풀이의 편의상 본 글에선 0~N-1로 둠
- 이때 총 이동 비용은, 해당 경로의 시작점을 어디로 두든 동일
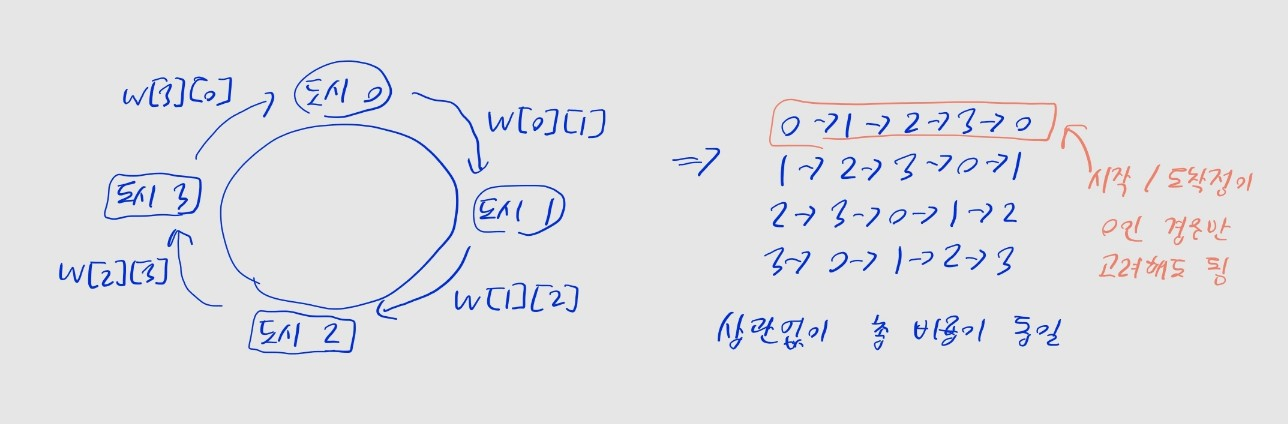
0 -> 1 -> 2 -> 3 -> 0 = W[0][1] + W[1][2] + W[2][3] + W[3][0]
1 -> 2 -> 3 -> 0 -> 1 = W[1][2] + W[2][3] + W[3][0] + W[0][1]
2 -> 3 -> 0 -> 1 -> 2 = W[2][3] + W[3][0] + W[0][1] + W[1][2]
3 -> 0 -> 1 -> 2 -> 3 = W[3][0] + W[0][1] + W[1][2] + W[2][3]
- 이동 비용 행렬을
W로 둘 때, 4가지 경로 모두 비용이 W[0][1] + W[1][2] + W[2][3] + W[3][0]으로 동일
- 따라서 중복되는 경우를 제외하기 위해, 도시 0을 시작점으로 고정하고, 나머지 지점들을 방문하는 순서의 경우의 수만 고려해도 됨
풀이
from itertools import permutations
N = int(input())
W = []
for _ in range(N):
W.append(list(map(int, input().split())))
def calc_cost(route):
route = [0, *route, 0]
cost = 0
for i in range(len(route) - 1):
start, end = route[i], route[i + 1]
if W[start][end] == 0:
return None
cost += W[start][end]
return cost
answer = float('inf')
for route in permutations(range(1, N)):
result = calc_cost(route)
if result:
answer = min(answer, result)
print(answer)
itertools.permuations(range(1, N))으로, 1부터 N-1까지의 수로 만들 수 있는 모든 순열을 확인
- 순열: 주어진 원소들을 모두 사용하여 만들 수 있는 서로 다른 순서의 조합
- 각 순열은
route 변수에 튜플 형태로 반환되며, 도시를 거치는 순서를 나타냄
- 실제 이동 경로에는 앞뒤에 출발점이자 도착점인 0번 도시를 붙여 줌
- e.g.,
N -> 4, route -> (1, 3, 2)인 경우, 도시 0 -> 1 -> 3 -> 2 -> 0 순으로 이동
check_total_cost(route)으로 해당 경로의 총 비용을 계산
[0, *route, 0]로 기존 route의 앞뒤에 원소 0을 추가한 리스트를 만듦- 도시 간 이동 비용을 모두 더해
cost 반환
- 단 특정 두 도시 간 비용이 0인 경우, 현재 경로로는 순회를 할 수 없으니
None 반환
- 모든
route에 대해 check_total_cost를 호출해, 최소값을 갱신 후 정답으로 반환
시간 복잡도
- 순열 만들기: 총 (N−1)!개의 순열이 만들어짐
- 각 순열에 대해 N번 비용을 계산하게 됨
- 최종 O(N×(N−1)!) = N!
- N≤10이므로, 계산하면 총 3,628,800번 계산됨 -> 2초 안에 충분히 가능
- 즉 이 문제는 브루트포스(완전 탐색)로도 충분히 풀 수 있음
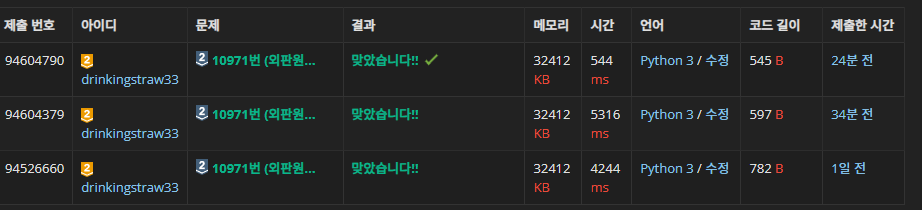
- 근데 사실 시작점을 고정 안 하고, 0번 도시까지 순열에 포함해도 문제가 풀리긴 했음
- 하지만 시작점을 고정할 때 풀이가 약 10배 빠름 (500ms vs 5000ms)
- 실제로 시작점을 고려하지 않는 경우, (N−1)!개의 순열이 아닌 N!개의 순열에 대해 비용을 계산하게 되므로, 연산량이 N배 많아짐
기억할 점
- N이 턱없이 작으면 걱정 말고 경우의 수를 전부 확인해 보자. 어차피 고생은 너가 아니라 컴퓨터가 한다.


