백준 / 실버 2 / 2805. 나무 자르기

- 대충 입력을 보니 무지막지하게 큰 숫자들이 보이네요
- N≤1,000,000....? M≤2,000,000,000....?
- 뭔가 시간 복잡도를 낮춰야 할 것 같은 삘이 오죠?
가져갈 수 있는 나무 길이 구하기
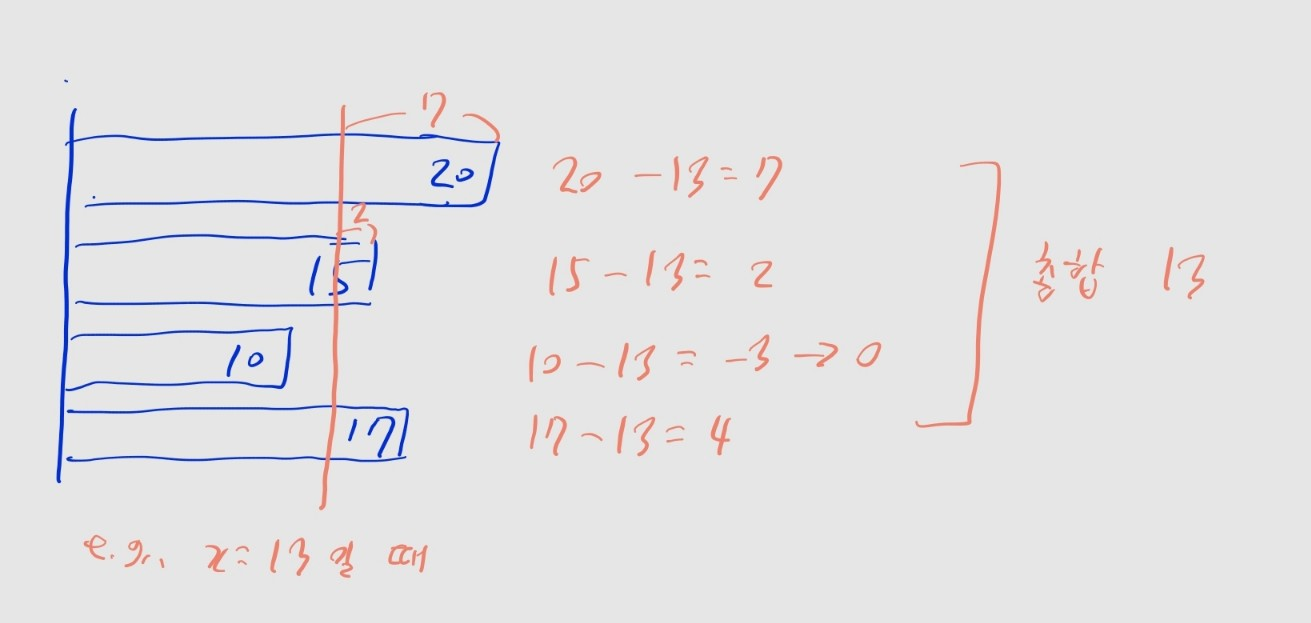
- 쉬운 것부터 합시다. 절단기의 높이를 매개변수
x로 받고, 가져갈 수 있는 나무 길이를 구하는 함수 cut_tree를 만들어보겠습니다.
- 나무를 자를 때,
(나무의 높이 - 절단기의 높이)만큼 가져갈 수 있습니다.
- 단, 나무보다 절단기의 높이가 높아서 음수가 되는 경우,
0으로 처리해야 합니다.
- 반복문으로 각 나무마다 가져갈 수 있는 길이를 계산하고, 모두 더해 반환합니다.
N, M = map(int, input().split())
trees = list(map(int, input().split()))
def cut_tree(x):
total = 0
for t in trees:
total += max((t - x), 0)
return total
- 나무의 수가 N일 때 위 함수의 시간 복잡도는 O(N)입니다.
범위 한정하기
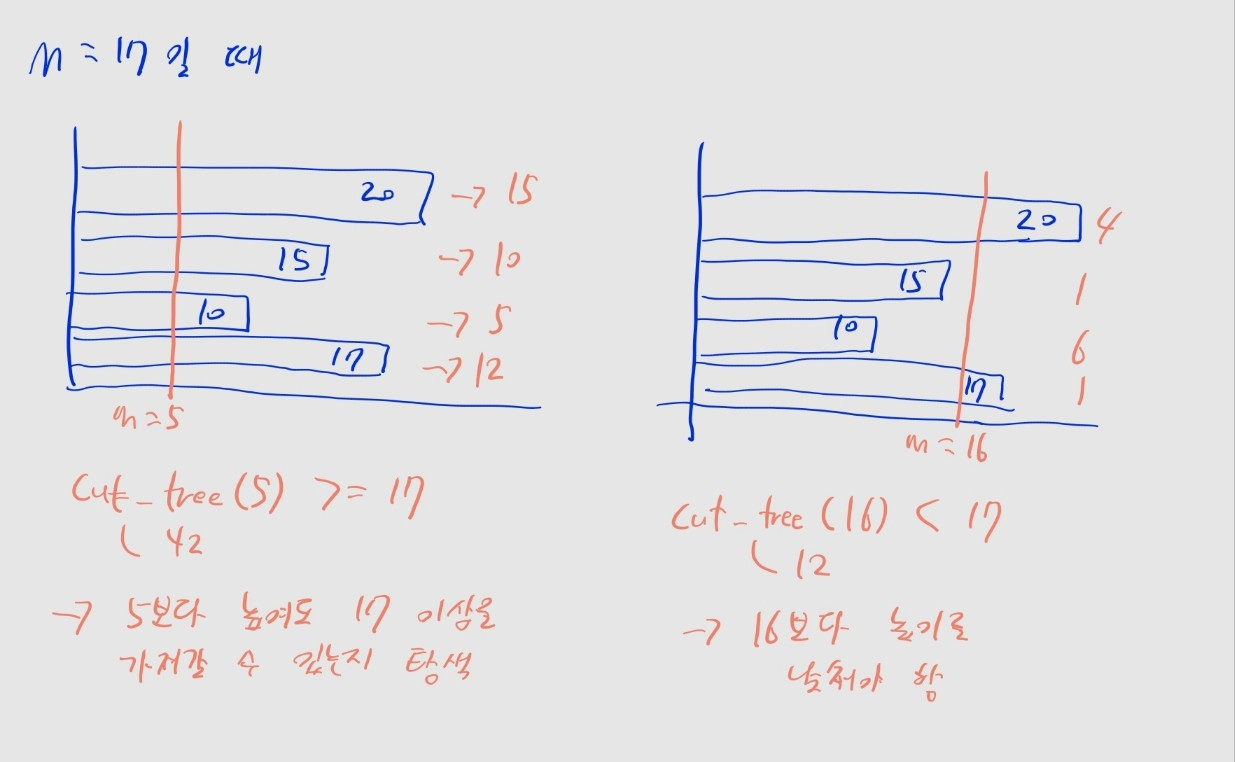
- 이 문제에선 절단기에 설정할 수 있는 높이의 최댓값을 구해야 합니다.
- 즉 일정 범위 내에서 정답을 탐색해야 하는데, 탐색 범위를 먼저 한정해야 합니다.

- 높이는 0부터 탐색해야 합니다.
- 이러면 그림처럼 나무 길이의 총합을 가져갈 수 있겠죠.
- 높이는 제일 높은 나무의 높이 (
max(trees))까지만 탐색하면 됩니다.
- 이러면 아무것도 가져가지 못합니다.
- 이것보다 높이를 높여도 아무것도 가져가지 못하는 건 똑같으니, 탐색하는 의미가 없습니다.
이분 탐색으로 정답 구하기
- 이제
x = 0부터 x = max(trees)까지 정수 중에서 정답을 찾으면 됩니다.
- 값 하나씩
cut_tree 함수에 넣으면서 정답을 찾으면 어떨까요? (선형 탐색)
max(trees)를 M으로, 나무의 수를 N으로 둘 때 O(M×N)- N≤1,000,000, M≤2,000,000,000인 만큼 100% 시간 초과가 뜹니다.
- 더 빠르게
x를 찾을 방법이 필요한데, O(logM)의 시간 복잡도를 갖는 이분 탐색을 사용할 수 있습니다.
- 흔히 이분 탐색을, 범위를 반씩 줄여 나가면서 배열에서 특정 값의 인덱스를 찾는 방법으로 아실 겁니다
- 대신 여기선 0부터 N-1까지의 인덱스가 아니라
0부터 max(trees)까지의 정수를 탐색합니다.
- 그리고 특정 값의 인덱스 가 아니라,
cut_trees(x) >= M를 만족하는 x의 최댓값*을 찾습니다.
l = 0
r = max(trees)
answer = 0
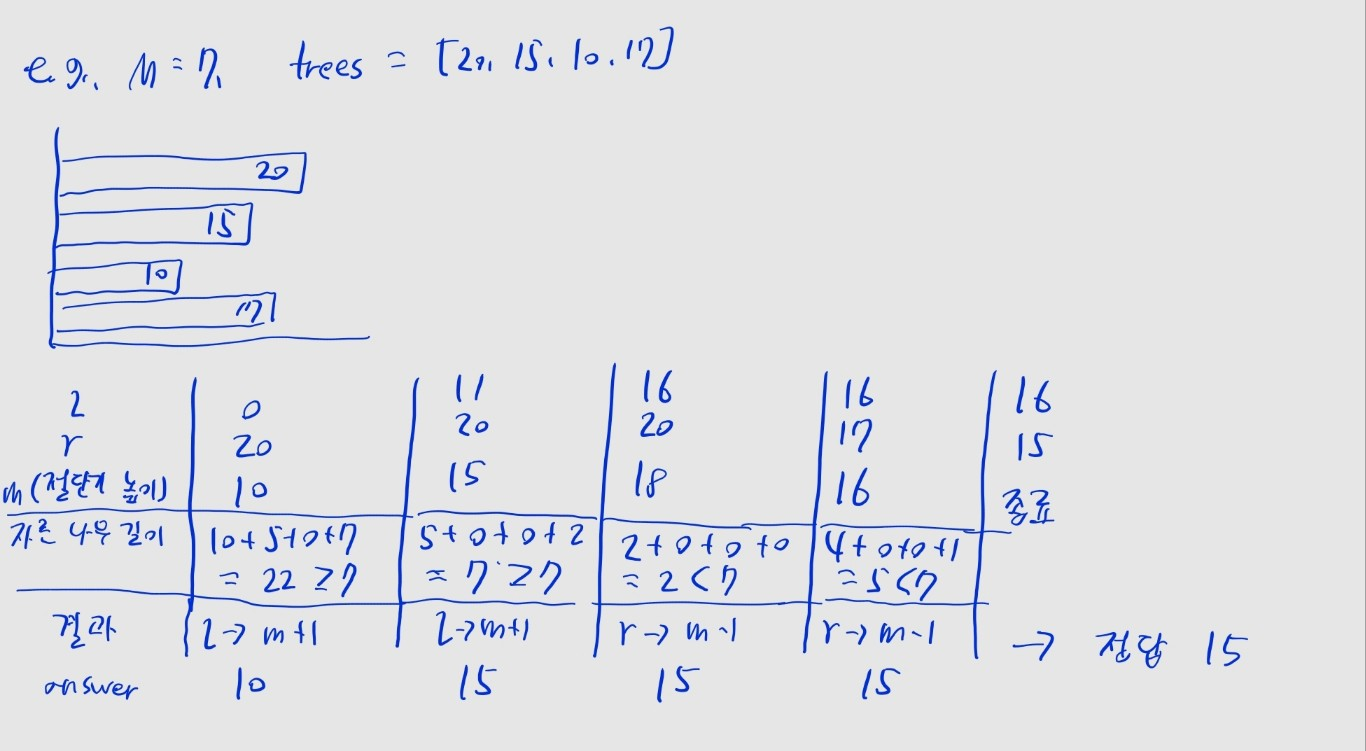
while l <= r:
m = (l + r) // 2
if cut_tree(m) >= M:
answer = max(answer, m)
l = m + 1
else:
r = m - 1
print(answer)
- 우선 앞서 구한 범위를 고려해
l을 0, r을 max(trees)로 설정합니다.
m <- (l + r) // 2로 두고, cut_tree(m)과 M의 값을 비교합니다.cut_tree(m) < M인 경우 너무 작게 잘랐으므로, 절단기 높이를 낮춰야 합니다.
r을 m - 1로 바꾼 뒤 다시 시도해봅니다.
cut_tree(m) >= M인 경우 M미터 이상을 잘라낼 수 있습니다.
- 하지만 이 문제에선 절단기 높이의 최댓값을 구해야 합니다.
- 즉 절단기 높이를 더 높여도 여전히
M미터 이상을 가져갈 수 있는지 확인합니다.
- 현재
m을 answer 변수에 정답 후보로 저장하고, l을 m + 1로 바꿔 시도해 봅니다.
l > r이 되면 탐색이 종료되고, answer에 담긴 높이 값이 정답입니다.
최종 풀이
N, M = map(int, input().split())
trees = list(map(int, input().split())) # 나무의 길이 저장
# 절단기 높이가 x미터일 때, 가져갈 수 있는 나무의 길이
def cut_tree(x):
total = 0
for t in trees:
total += max((t - x), 0)
return total
# 0미터와 (나무 중 최고 높이)미터 사이에서 정답을 찾기
l = 0
r = max(trees)
answer = 0 # 정답 (절단기 높이의 최대값)
while l <= r:
m = (l + r) // 2
# M미터 이상을 가져갈 수 있음
# -> 절단기의 높이를 높여도, M미터 이상을 가져갈 수 있나?
if cut_tree(m) >= M:
answer = max(answer, m)
l = m + 1
# M미터 이상을 가져갈 수 없음
# -> 절단기의 높이를 낮춰야 함
else:
r = m - 1
print(answer)
시간 복잡도
- 나무의 개수를 N으로, 나무 길이 중 최댓값을 M으로 둘 때,
cut_tree 함수 (잘린 나무 길이 계산)의 시간 복잡도는 O(N)- 이진 탐색에서 총 O(logM)회
cut_tree 함수가 실행됨
- 최종 O(NlogM)
- N≤1,000,000, M≤2,000,000,000
- 하지만 보통 O(logM)은 상당히 작은 값이니 무시해도 됨
- 실제로, log22,000,000,000은 약 30
- 즉 충분히 1초 안에 풀 수 있다~
기억할 점
- 탐색해야 하는 범위가 기상천외하게 넓은 경우, 이진 탐색 문제로 바꿔서 생각해 보자.





