레드블랙 트리는 레드벨벳이랑 블랙핑크가 식목일날 심은 나무입니다.

참고 자료

• 레드블랙트리(red-black tree)의 기본 개념과 특징 (유튜브 <쉬운코드>)
• 좌충우돌, 파이썬으로 자료구조 구현하기 (심명수)

본 글은 간결성을 위해 엄밀한 증명, 검증은 생략했습니다. 그런 부분이 궁금하시면 참고 자료 시청을 권해 드립니다.

레드 블랙 트리

• 스스로 균형을 잡는 이진 탐색 트리
  • 균형: 트리의 구조가 너무 한 쪽으로 치우치지 않도록 유지하는 것

시간 복잡도

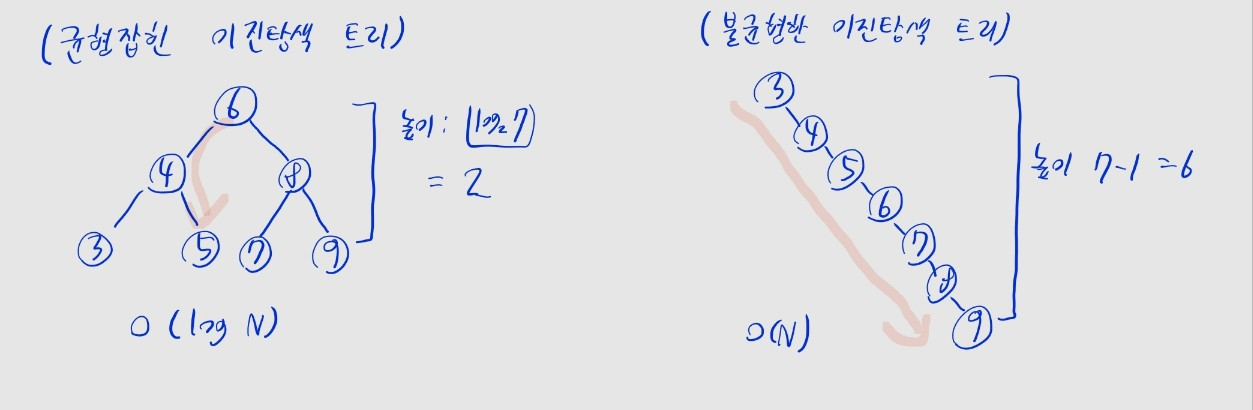
• 일반적인 이진 탐색 트리의 탐색 / 삽입 / 삭제 시간 복잡도
  • 트리가 균형잡혔을 때: 평균 $O(\log N)$
  • 트리가 균형잡히지 않았을 때: 최악 $O(N)$
  • 즉, 한쪽 방향에만 계속 노드가 삽입되어, 선형 리스트와 다를 바 없는 경우 $O(N)$이 소요됨
• 레드 블랙 트리는 스스로 균형을 잡기 때문에, 최악의 경우에도 탐색 / 삽입 / 삭제 시 $O(\log N)$의 시간 복잡도를 유지함

회전 연산

• 레드블랙 트리의 삽입 연산을 이해하려면, 회전을 확실히 이해할 필요가 있음
• 이진탐색 트리가 한 쪽으로 치우쳐 있을 때 균형을 맞추는 연산
  • 트리의 모양은 달라지지만, 이진탐색 트리의 성질 (왼쪽 < 부모< 오른쪽)은 유지됨
• 특정 노드를 기준으로, 우회전 및 좌회전 가능

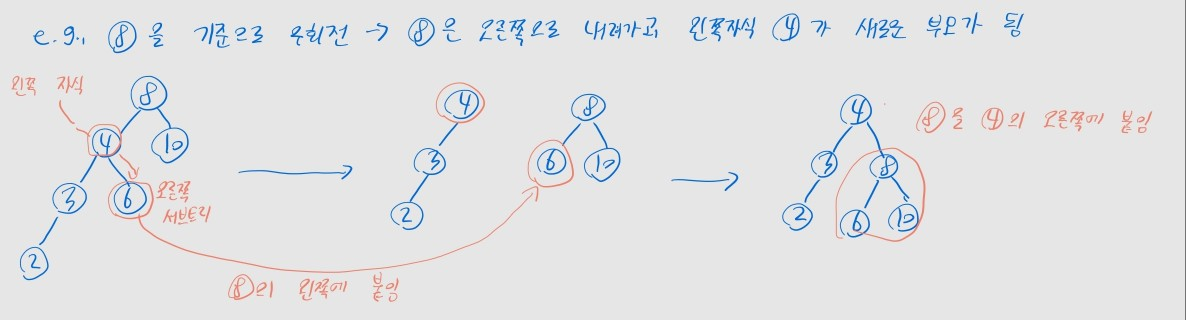
우회전 연산

• 트리가 왼쪽으로 치우쳐 있을 때 사용

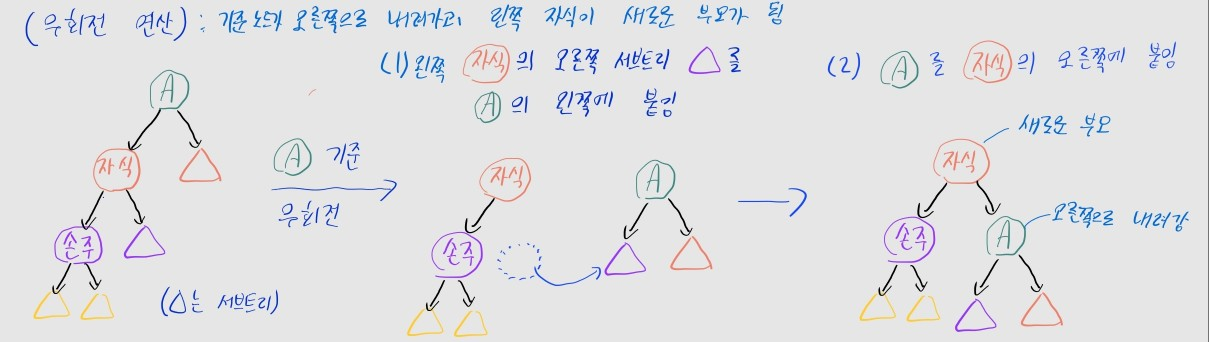
• 기준 노드가 오른쪽으로 내려가고, 왼쪽 자식이 새로운 부모가 됨
• 절차
  • (1) 왼쪽 자식의 오른쪽 서브트리를, 기준 노드의 왼쪽에 붙임
  • (2) 기준 노드를 왼쪽 자식의 오른쪽에 붙임

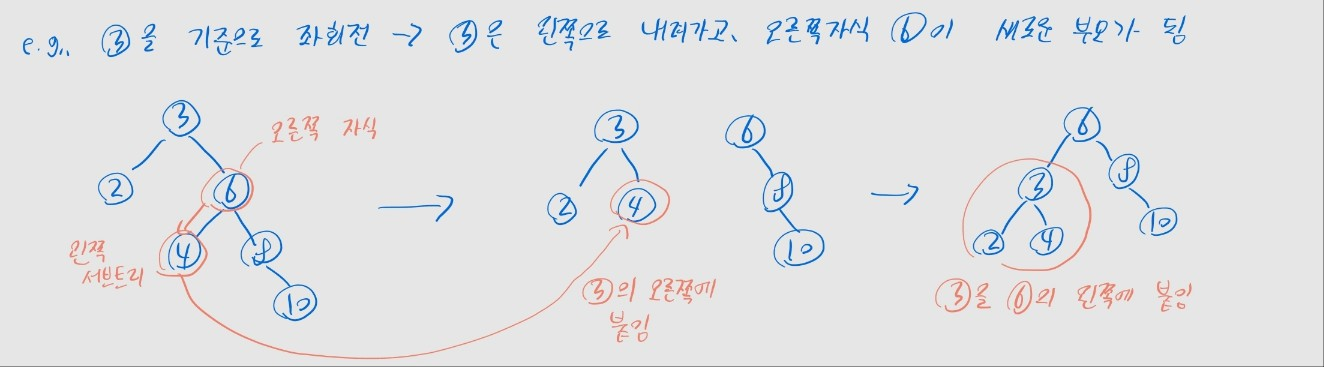
좌회전 연산

• 트리가 오른쪽으로 치우쳐 있을 때 사용

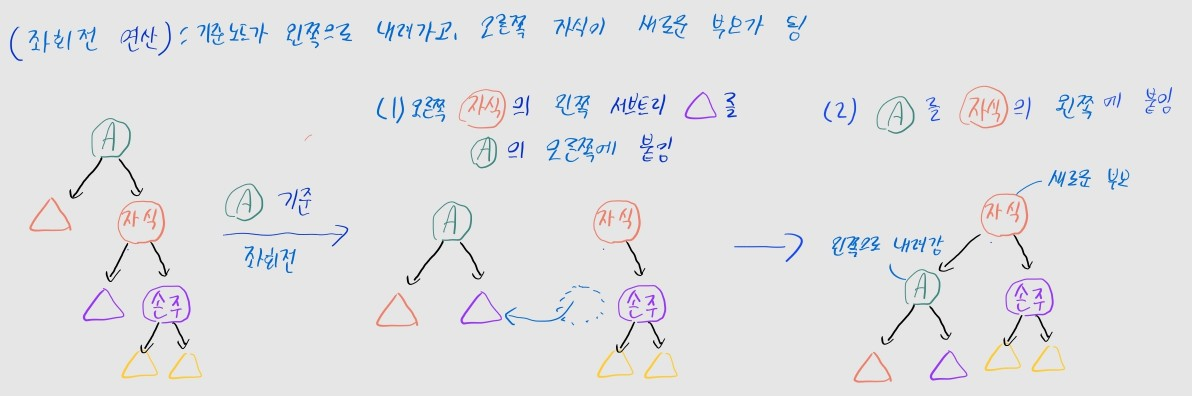
• 기준 노드가 왼쪽으로 내려가고, 오른쪽 자식이 새로운 부모가 됨
• 절차
  • (1) 오른쪽 자식의 왼쪽 서브트리를, 기준 노드의 오른쪽에 붙임
  • (2) 기준 노드를 오른쪽 자식의 왼쪽에 붙임

⚠️ 너무 어려우면 기준 노드가 회전한 방향으로 내려가고, 그 자리를 기준 노드의 자식이 채운다 정도만 기억해도 충분합니다.

레드 블랙 트리의 속성

• 총 5가지의 속성이 존재
  • 삽입, 삭제 시 위반되는 속성이 있으면, 이를 해결하기 위해 구조를 바꿈

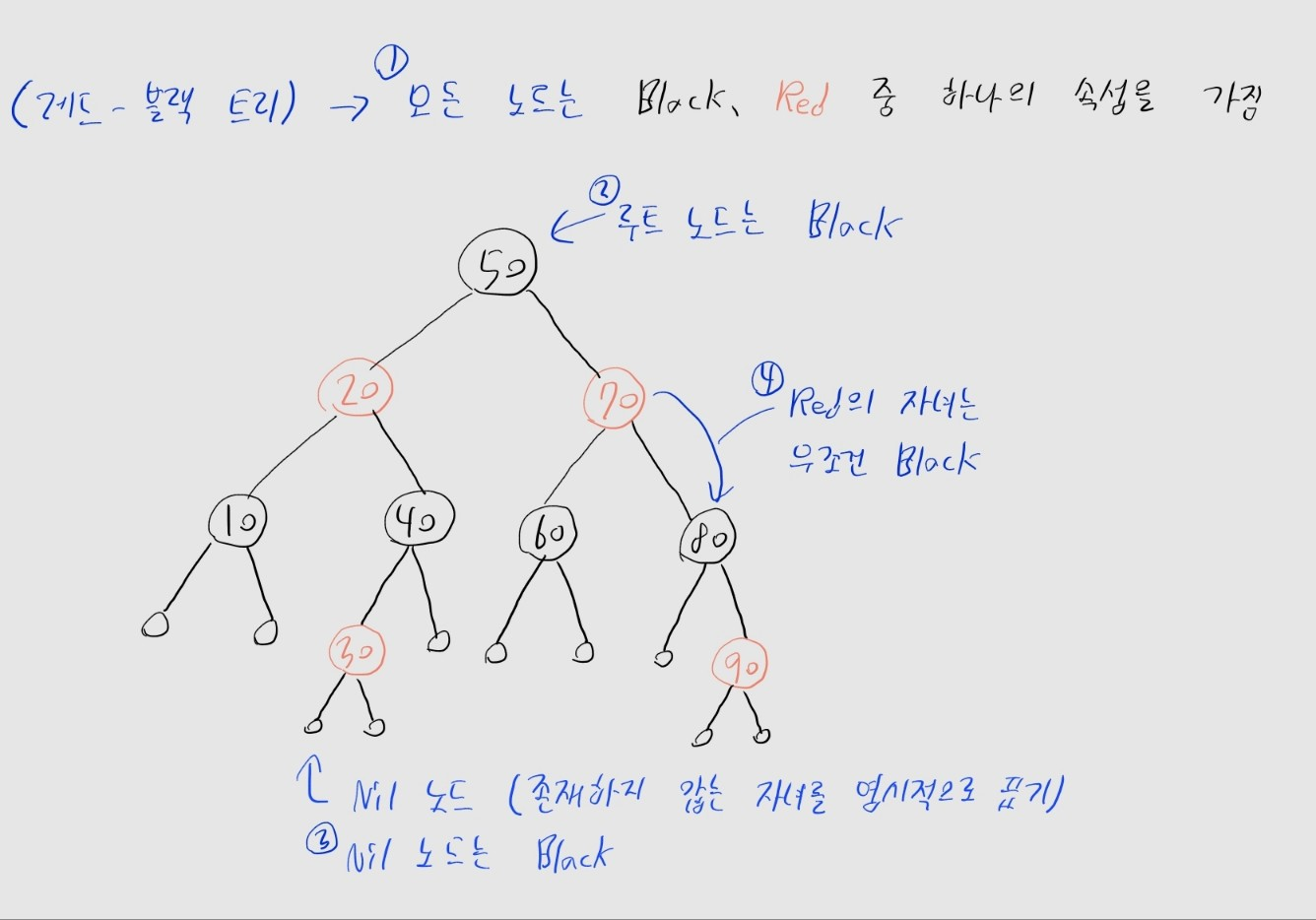
• (1) 모든 노드는 Red / Black 중 하나의 속성을 가짐
• (2) 루트 노드는 Black 노드
  • 루트 노드는 Black 노드
• (3) 모든 Nil 노드는 Black 노드
  • 자식이 없을 때, 존재하지 않는 자식을 Nil 노드로 표기
  • 레드 블랙 트리의 리프 노드는 Nil 노드
• (4) Red 노드의 자식는 무조건 Black 노드
  • Red가 연속으로 존재할 수 없음

Black Height

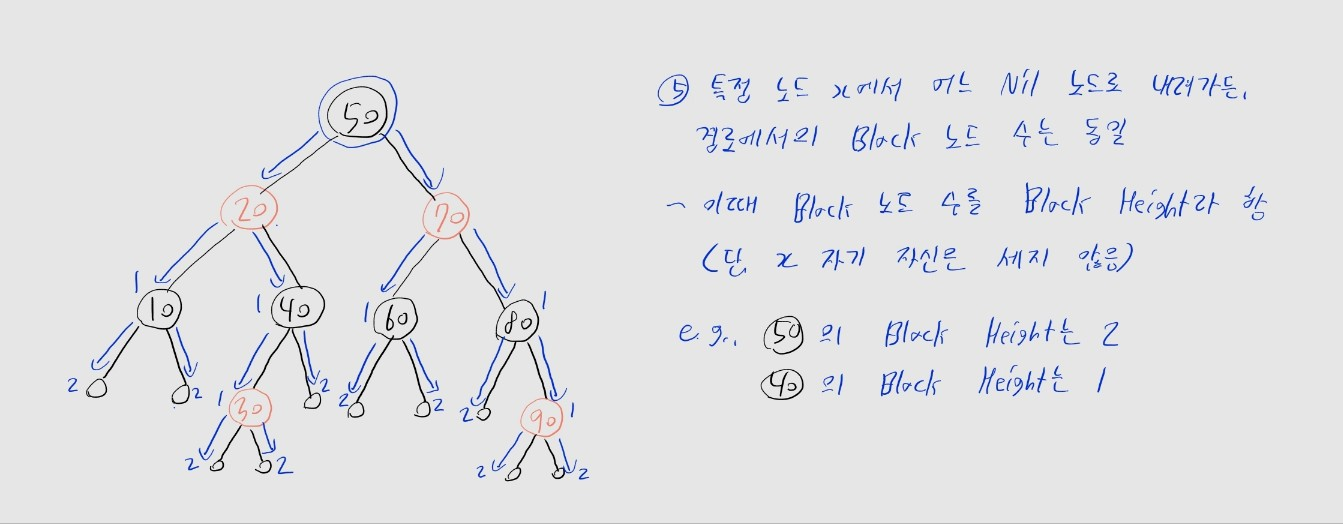
• (5) 특정 노드 x에서 어느 Nil 노드로 내려가든, 경로에서 마주치는 Black 노드 수는 동일
  • 이때 Black 노드 수를 Black Height라 함
  • 단, x가 Black인 경우, x 자기 자신은 세지 않음
• 두 자식이 같은 색일 때, 부모와 자식의 색을 맞바꿔도 속성 (5)가 유지됨
  • 삽입, 삭제 때 많이 쓰이는 특징이니 기억하기

삽입

• 삽입은 이진 탐색 트리와 동일하게 이루어짐
  • 삽입 노드와 현재 노드의 값을 비교하며, 삽입할 적절한 위치를 찾기
  • 이때 삽입 노드는 Red, 삽입한 노드의 자식인 Nil 노드는 Black으로 설정
• 단, 삽입 후 RB 트리 속성이 위반되면 이를 조정해 주어야 함
  • 1번 (Red / Black으로 이루어짐), 3번 (Nil 노드는 Black)은 위반할 일이 없음

⚠️ 편의상 이제부터 Nil 노드를 그림에선 생략하겠습니다.

• 보통은 2번, 4번 속성을 위반하게 됨
  • 2번 (루트 노드가 Red일 때) 위반 -> 단순히 Red에서 Black으로 바꿔주면 그만
  • 4번 (삽입한 노드의 부모가 Red일 때 연속) 위반 -> 이 경우 꽤나 복잡해짐
• 5번 속성 (Black Height가 일정)은 대놓고 위반했는지 바로 확인하기는 어려움
• 이러한 상황에선 트리의 구조를 변경해야 함
  • 이진 탐색 트리의 성질을 유지하는 동시에
  • 5번 속성이 추가로 위반되지 않게 수정하는 방법을 사용

부모, 자식이 연속으로 Red일 때

• Red 노드를 삽입했는데, 부모에도 Red가 존재하면 4번 속성을 위반하니 수정해야 함
• 일단 부모의 형제의 색이 Red인지 Black인지 확인
  • 앞으로는 '부모의 형제'를 편의상 삼촌 노드로 부르겠습니다

⚠️ 삼촌이 없는 경우, Nil 노드로 취급되기 때문에 Black입니다.

삼촌의 색	삽입 위치	부모의 위치	사례
Red	상관없음	상관없음	Case 1
Black	왼쪽	왼쪽	Case 2
Black	오른쪽	오른쪽	Case 2
Black	왼쪽	오른쪽	Case 3
Black	오른쪽	왼쪽	Case 3

사례 1: 삼촌이 Red일 때

• (1) 부모와 삼촌을 Black으로 바꾸고, 조부모를 Red로 바꿈
• (2) 조부모를 확인하여 위반된 속성이 있는지 확인. 위반된 속성이 있으면 수정
  • (e.g., 조부모가 Red로 바뀌었는데 루트였다면, 2번 속성을 위반하기 때문에 Black으로 바꿔 줘야 함)

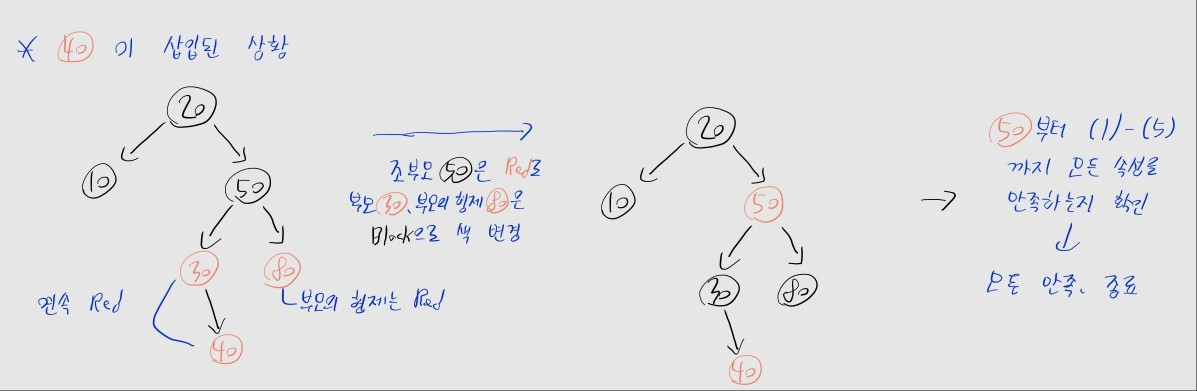
• 우선 삽입한 40의 삼촌을 확인 -> 40의 삼촌은 80이구나. 색을 확인하니 Red네?
• 부모 30, 삼촌 80은 black으로, 조부모 50은 red로 색 바꾸기
• 이후 조부모 50가 위반되는 속성이 없나 다시 확인
  • 위반 속성이 없으므로, 확정

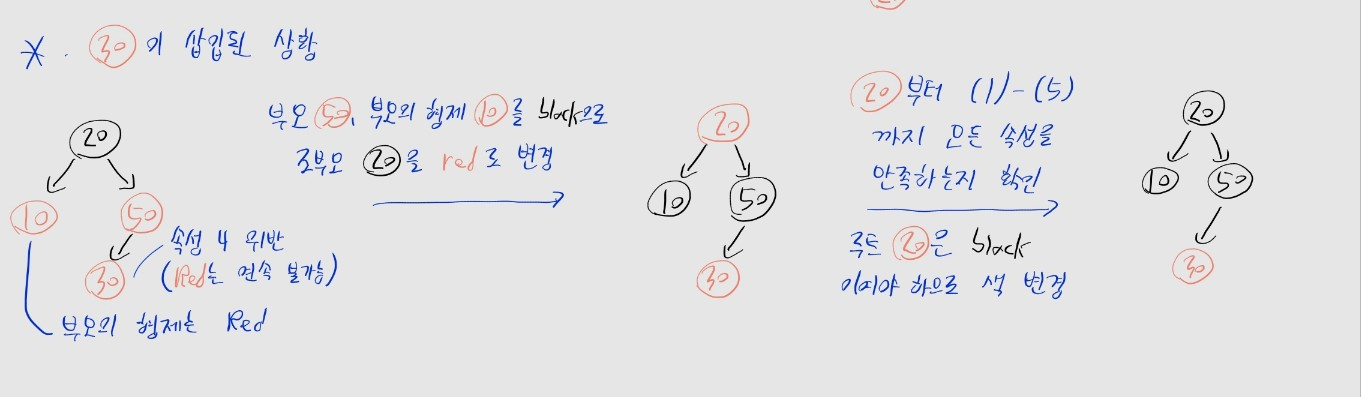
• 우선 삽입한 30의 삼촌을 확인 -> 30의 삼촌은 10이구나. 색을 확인하니 Red네?
• 부모 50, 삼촌 10은 black으로, 조부모 20은 red로 색 바꾸기
• 이후 조부모 20이 위반되는 속성이 없나 다시 확인
  • 20이 루트 노드인데, red이므로 2번 조건 위배 -> black으로 바꿔줌
  • 그 외 위반 속성이 없으므로, 확정

사례 2: 삼촌이 Black일 때

• 이 경우, 삽입된 노드는 부모의 왼쪽 자식인지, 오른쪽 자식인지 확인
• 그리고 부모는 조부모의 왼쪽 자식인지, 오른쪽 자식인지 확인
• 방향이 일치하는지 불일치하는지에 따라 이후 연산이 달라짐

2A. 방향이 일치하는 경우

• 삽입된 노드가 부모의 왼쪽 자식이며, 부모는 조부모의 왼쪽 자식인 경우
  • (1) 부모와 조부모의 색을 바꾼 후,
  • (2) 조부모 기준으로 우회전하기
• 삽입된 노드가 부모의 오른쪽 자식이며, 부모는 조부모의 오른쪽 자식인 경우
  • (1) 부모와 조부모의 색을 바꾼 후
  • (2) 조부모 기준으로 좌회전하기
• 사례 1과 달리 무조건 5개 속성을 모두 만족하므로, 다시 확인할 필요는 없음
  • 회전과 색 변경을 하는 과정에서 5번 속성이 유지됨

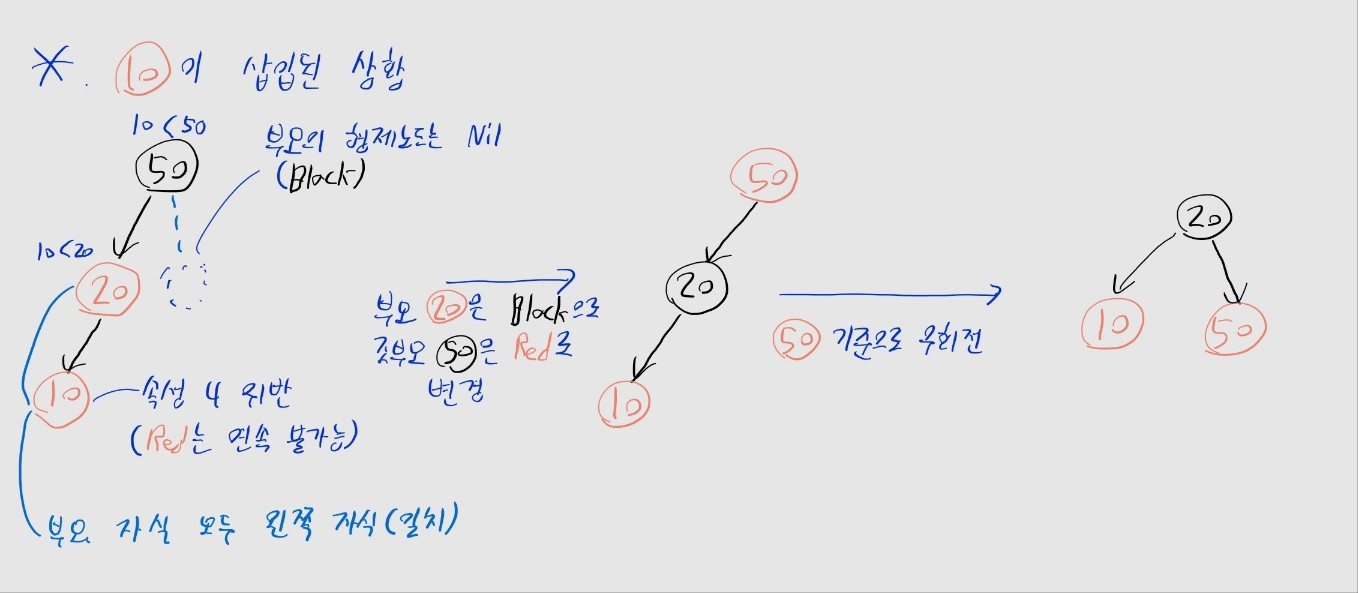
• 우선 삽입한 10의 삼촌을 확인 -> 없네? Nil이니까 Black이겠지?
• 10은 부모 20의 왼쪽 자식, 부모 20은 조부모 50의 왼쪽 자식 -> 방향이 똑같네?
• 이후 부모 20과 조부모 50의 색을 바꾼 후, 조부모 50을 기준으로 우회전하면 됨

2B. 방향이 불일치하는 경우

• 삽입된 노드가 부모의 오른쪽 자식이며, 부모는 조부모의 왼쪽 자식인 경우
  • (1) 부모 기준으로 좌회전한 뒤
  • (2) 부모와 조부모의 색을 바꾼 후,
  • (3) 조부모 기준으로 우회전하기
• 삽입된 노드가 부모의 왼쪽 자식이며, 부모는 조부모의 오른쪽 자식인 경우
  • (1) 부모 기준으로 우회전한 뒤
  • (2) (새로운) 부모와 조부모의 색을 바꾼 후
  • (3) 조부모 기준으로 좌회전
• 사례 1과 달리 무조건 5개 속성을 모두 만족하므로, 다시 확인할 필요는 없음
  • 회전과 색 변경을 하는 과정에서 5번 속성이 유지됨

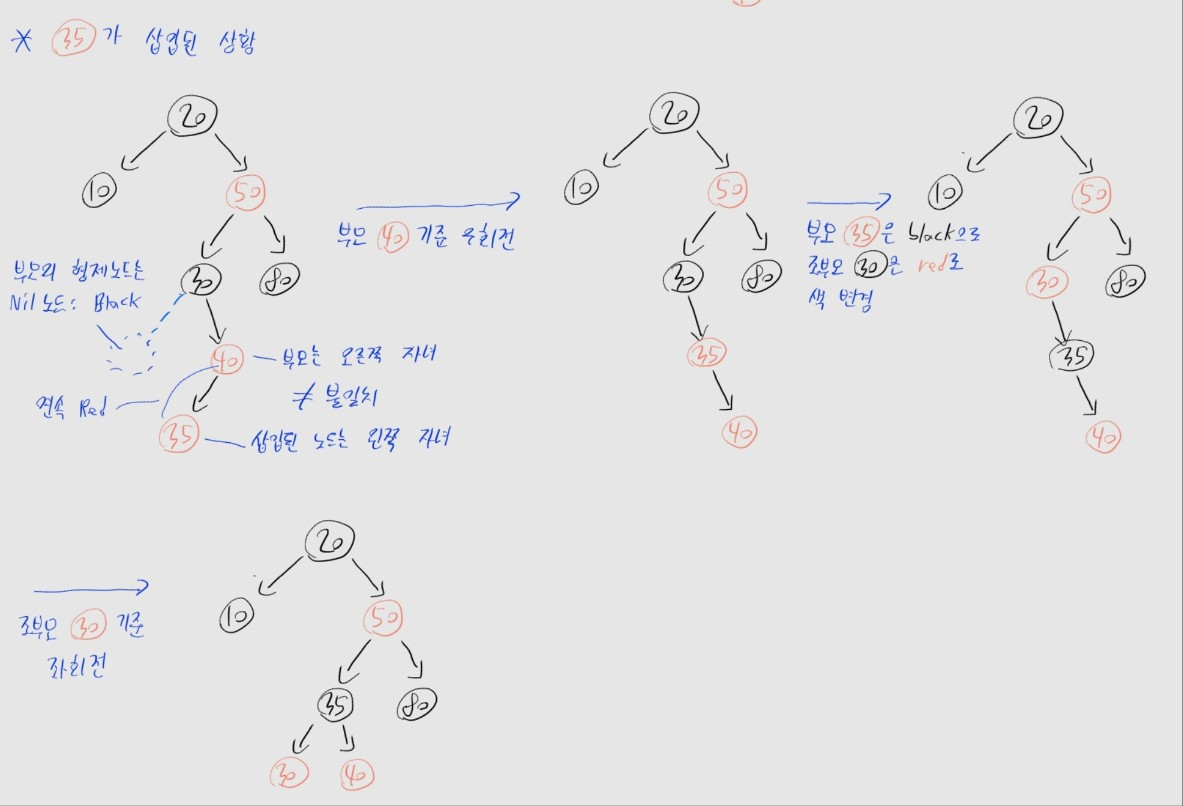
• 우선 삽입한 35의 삼촌을 확인 -> 없네? Nil이니까 Black이겠지?
• 35는 부모 40의 왼쪽 자식, 부모 40은 조부모 30의 오른쪽 자식 -> 방향이 엇갈리네?
• 우선 부모 40 기준으로 우회전
• 이후 (새로운) 부모 35와, 조부모 30의 색을 바꾼 후, 조부모 30을 기준으로 좌회전

꽤나 복잡한 삽입 예제

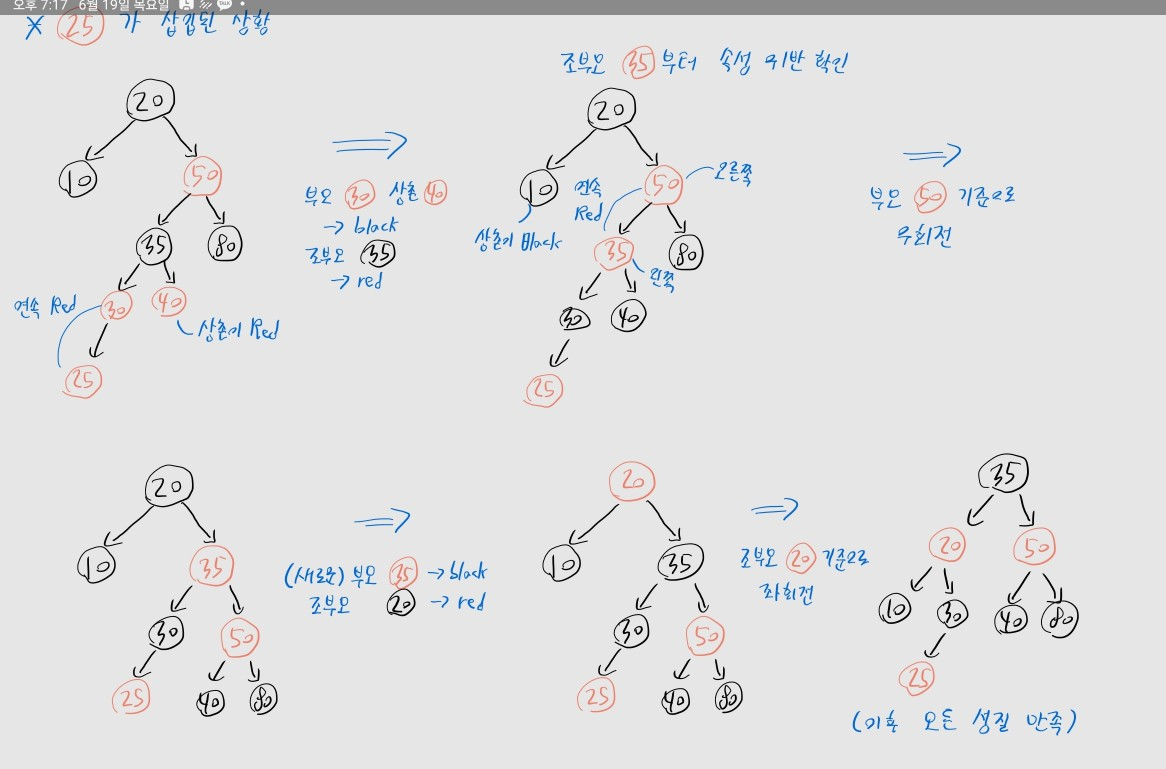
• 위 사례에선, 25를 삽입함
  • 우선 삽입한 25의 삼촌을 확인 -> 삼촌 40은 Red네?
  • 따라서 부모 30, 삼촌 40은 Black으로, 조부모 35는 Red로 변경
• 이후 조부모 35의 규칙 위반을 확인
  • 35이 Red인데 50도 Red이므로 연속으로 Red가 옴, 4번 속성 위반
• 이 부분 역시 수정해야 함
  • 우선 규칙이 위배된 35의 삼촌을 확인 -> 삼혼 10은 Black이네?
  • 30은 왼쪽 자식이고, 부모 50은 오른쪽 자식 -> 엇갈리네?
• 이제 사례 2-방향이 불일치하는 경우와 동일하게 수정
  • 부모 50을 기준으로 우회전한 뒤
  • 새로운 부모 35, 조부모 20의 색을 바꾼 뒤
  • 조부모 20을 기준으로 좌회전
• 이후엔 모든 속성이 유지되므로, 추가 수정할 필요 없음