안정적으로 빠른 속도를 보장하는 병합 정렬과 힙 정렬, 제한된 범위의 중복 값을 정렬할 때 효과적인 도수 정렬을 정리해 보았다.

정렬	설명	시간복잡도	공간복잡도	안정성
병합 정렬	배열을 두 그룹으로 나누어 각각 재귀적으로 정렬 후 병합	$O(N \log N)$	$O(N)$	O
힙 정렬	최대 힙 자료구조를 사용한 정렬 방법	$O(N \log N)$	$O(N)$	X
도수 정렬	값을 비교하는 대신, 값의 개수를 셈	$O(N + K)$ ($K$는 데이터값의 범위)	$O(N+K)$	O

병합 정렬

• 배열을 앞부분, 뒷부분 두 그룹으로 나누어 각각 정렬 후 병합하는 과정을 반복

정렬된 두 배열 병합하기

• 정렬된 배열 A, B의 각각 맨 앞에서 시작하는 포인터 i, j를 둠
• A[i], B[j] 중 작은 값을 새로운 배열 C에 추가
• 값을 추가한 배열의 포인터를 1 증가
• 한쪽 배열의 원소가 모두 추가되면, 나머지 배열의 원소를 모두 추가

def merge_sorted_list(a, b, c):
    i, j, k = 0, 0, 0
    na, nb, nc = len(a), len(b), len(c)

    # 두 배열의 원소 비교
    while i < na and j < nb:
        if a[i] <= b[j]:
            c[k] = a[i]
            i += 1
        else:
            c[k] = b[j]
            j += 1
        k += 1

    # 한 쪽이 끝나면, 나머지 배열의 값을 모두 복사
    while i < na:
        c[k] = a[i]
        i += 1
        k += 1

    while j < nb:
        c[k] = b[j]
        j += 1
        k += 1

a = [2, 4, 6, 8, 11, 13]
b = [1, 2, 3, 4, 9, 16, 21]
c = [None] * (len(a) + len(b))
merge_sorted_list(a, b, c)
print(c)  # [1, 2, 2, 3, 4, 4, 6, 8, 9, 11, 13, 16, 21]

• 시간 복잡도: 두 배열의 원소 수 합이 $N$일 때, $O(N)$

병합 정렬

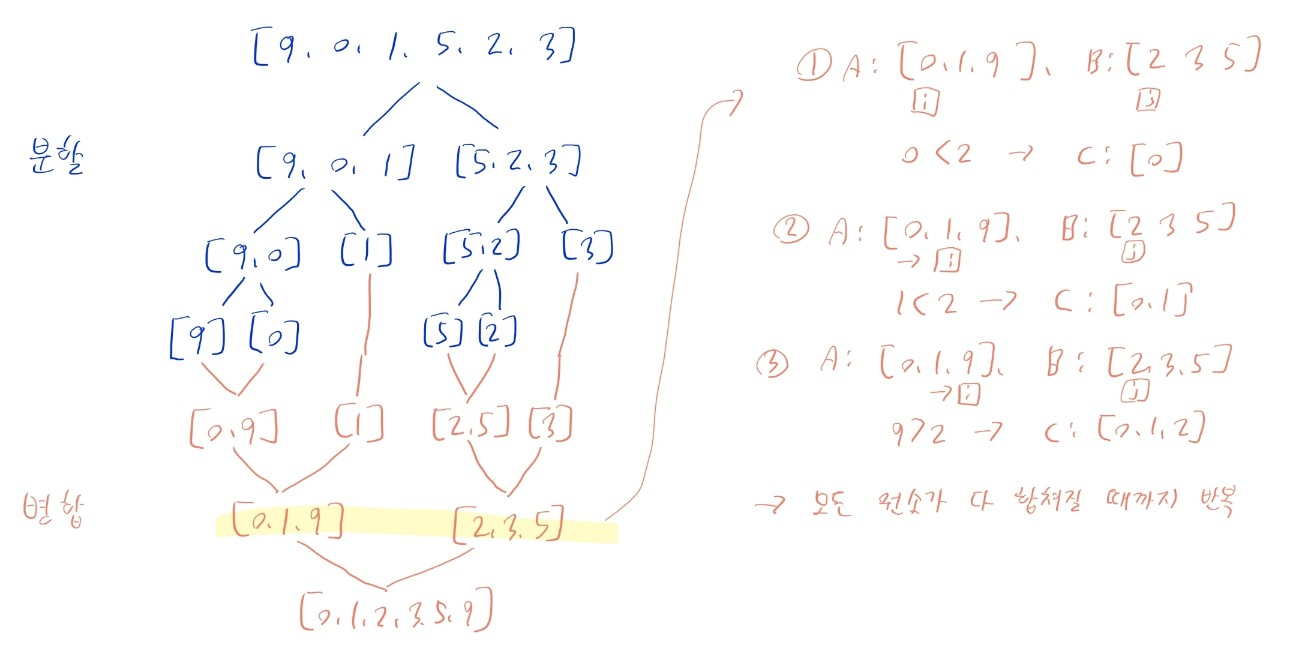
• (1) 배열을 절반으로 나눔
  • 앞부분을 병합 정렬로 정렬 (재귀)
  • 뒷부분을 병합 정렬로 정렬 (재귀)
• (2) 정렬된 두 부분 배열을 병합
• 단 배열의 길이가 1인 경우, 이미 정렬된 상태이므로 더 분할하지 않음

def div_and_merge(a, temp, start, end):
    if start < end:
        center = (start + end) // 2
        div_and_merge(a, temp, start, center)
        div_and_merge(a, temp, center + 1, end)

        i = start
        j = center + 1
        k = start

        while i <= center and j <= end:
            if a[i] <= a[j]:
                temp[k] = a[i]
                i += 1
            else:
                temp[k] = a[j]
                j += 1
            k += 1

        while i <= center:
            temp[k] = a[i]
            i += 1
            k += 1

        while j <= end:
            temp[k] = a[j]
            j += 1
            k += 1

        for x in range(start, end + 1):
            a[x] = temp[x]
            
def merge_sort(a):
   n = len(a)
   temp = [0] * n
   div_and_merge(a, temp, 0, n - 1)

a = [1, 3, 12, 6, 4, 11, 8, 7, 3, 2, 6, 5]
merge_sort(a)
print(a)  # [1, 2, 3, 3, 4, 5, 6, 6, 7, 8, 11, 12]

시공간 복잡도 및 안정성

시간 복잡도

• 데이터 원소 수가 $N$일 때
• 매번 배열을 반으로 나누므로, 총 $log_2(N)$단계가 필요함
• 각 단계에서 전체 데이터를 1번씩 확인하며 병합을 진행하므로, $O(N)$의 시간 소요
• 총 $O(N \log N)$, 입력 데이터와 상관없이 시간 복잡도가 안정적
  • 최악의 경우에도 $O(N \log N)$
  • $O(N^2)$까지 소요 시간이 증가할 수 있는 퀵 정렬과 비교했을 때 큰 장점

공간 복잡도

• 최대 재귀 깊이만큼 함수 호출 정보를 저장할 공간 필요 -> $\log N$
  • 🤔 함수 내에서 재귀 호출이 2회 이루어지는 만큼, 실제 함수 호출 횟수는 $\log N$번보다 많지 않나요?
  • 😾 공간 복잡도를 계산할 땐 최대 재귀 깊이를 반영하지, 총 재귀 횟수를 반영하지 않습니다. 먼저 호출된 함수가 종료되어야 두 번째 호출이 실행되므로, 두 호출이 같은 시점에 동시에 메모리에 남아 있지 않습니다. 따라서 재귀 호출을 하면서 쌓이는 최대 깊이 $\log N$이 기준이 됩니다.
• 병합된 값을 저장할 temp 배열 생성 -> $N$
• 최종 $O(N + \log N)$ -> $O(N)$

안정성

• 서로 떨어져 있는 원소를 교환하지 않으므로 안정적
  • 단 두 배열의 병합 과정에서, 두 포인터가 가리키는 원소의 값이 동일한 경우 앞쪽 배열의 원소를 먼저 추가해야 함
  • a[i] <= b[j]로 조건문을 설정한 이유

힙 정렬

힙

• 힙: 부모의 값이 자식의 값보다 항상 큰 완전 이진 트리
  • 이진 트리: 자식을 최대 2개 갖는 노드로 이루어진 트리
  • 완전 이진 트리: 마지막 층을 제외하면 모든 노드가 채워져 있고, 마지막 층만 왼쪽부터 차례로 채워진 트리
• 힙의 최댓값은 루트(맨 위 노드)에 저장되어 있음
• 힙의 부모 자식 대소관계는 일정하지만, 형제 간의 대소 관계는 일정하지 않음
• 힙은 배열로 표현 가능
  • 현재 노드 -> a[i]
  • 부모 노드 -> a[(i - 1) // 2]에 저장됨
  • 자식 노드 -> a[2 * i + 1](좌), a[2 * i + 2](우)

힙의 재구성

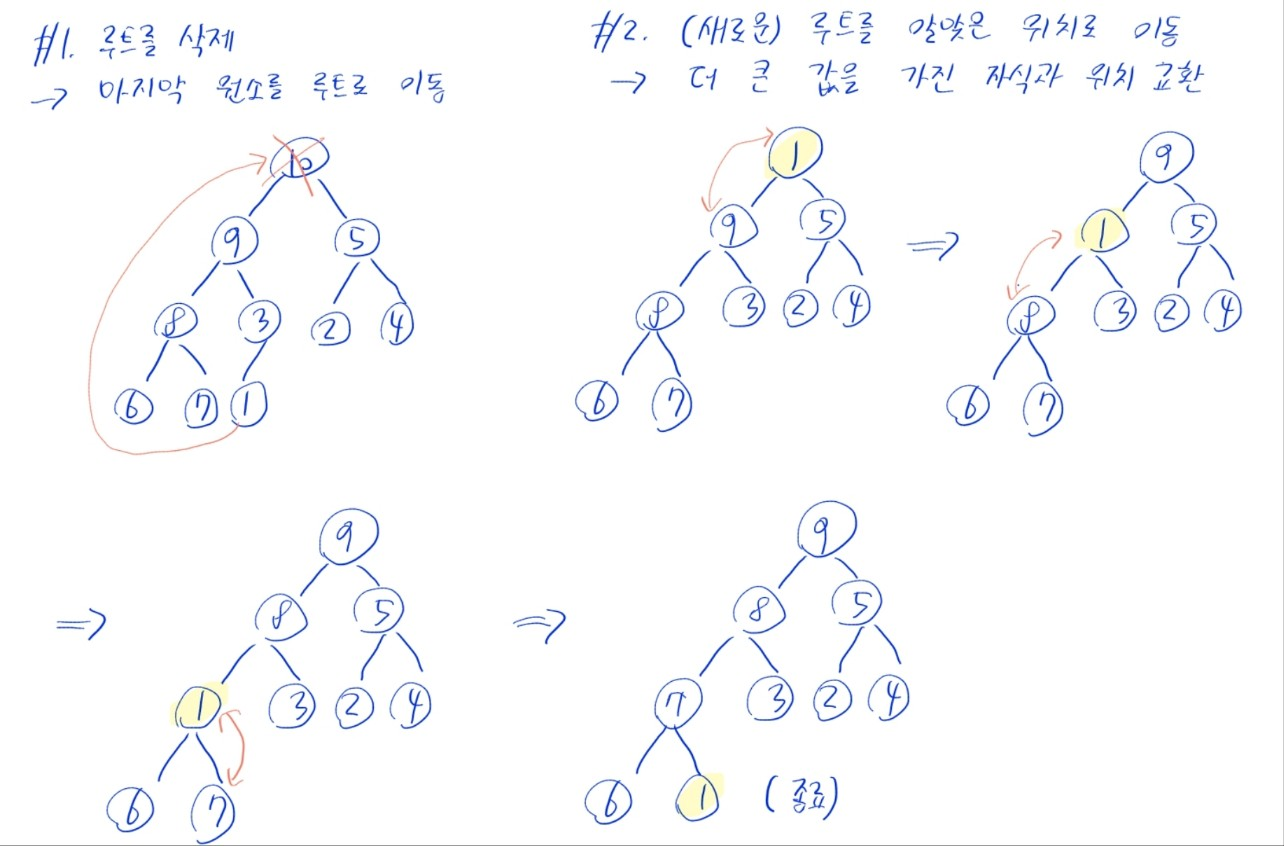
• 힙 정렬은 매번 힙의 루트를 꺼내고, 남은 원소들을 다시 힙으로 만드는 재구성 작업을 반복함
• (1) 루트 꺼내기
• (2) 마지막 원소(제일 하단 오른쪽)를 루트로 이동
• (3) (새로운) 루트에서 시작하여, 자신보다 큰 값을 가진 자식과 자리를 바꾸며 아래로 내려가는 작업 반복
  • 두 자식의 값이 모두 자신보다 크면, 둘 중에 더 큰 자식과 자리를 바꿈
  • 두 자식의 값이 모두 자신보다 작으면 종료
  • 맨 밑 층에 도달해도 종료
• 즉, 남은 힙의 원소 중 최대값을 루트로 만들어 주는 작업으로도 볼 수 있음

힙 정렬 알고리즘

• (1) 정렬되지 않은 구역의 맨 끝 원소를 나타내는 포인터 i를 n-1로 초기화
• (2) 배열 a의 a[0] (루트)와 a[i]를 교환
• (3) a[0]...a[i-1]을 힙으로 재구성
  • a[0](루트)에서 시작하여, 자신보다 큰 값을 가진 자식과 자리를 바꾸며 아래로 내려가는 작업 반복
  • (2), (3)단계가 앞선 힙의 재구성 에서 다루었던 부분
• (4) i의 값을 1 감소한 뒤, (2)로 돌아가 반복
  • i == 0일 때 정렬 완료

배열을 힙으로 만들기

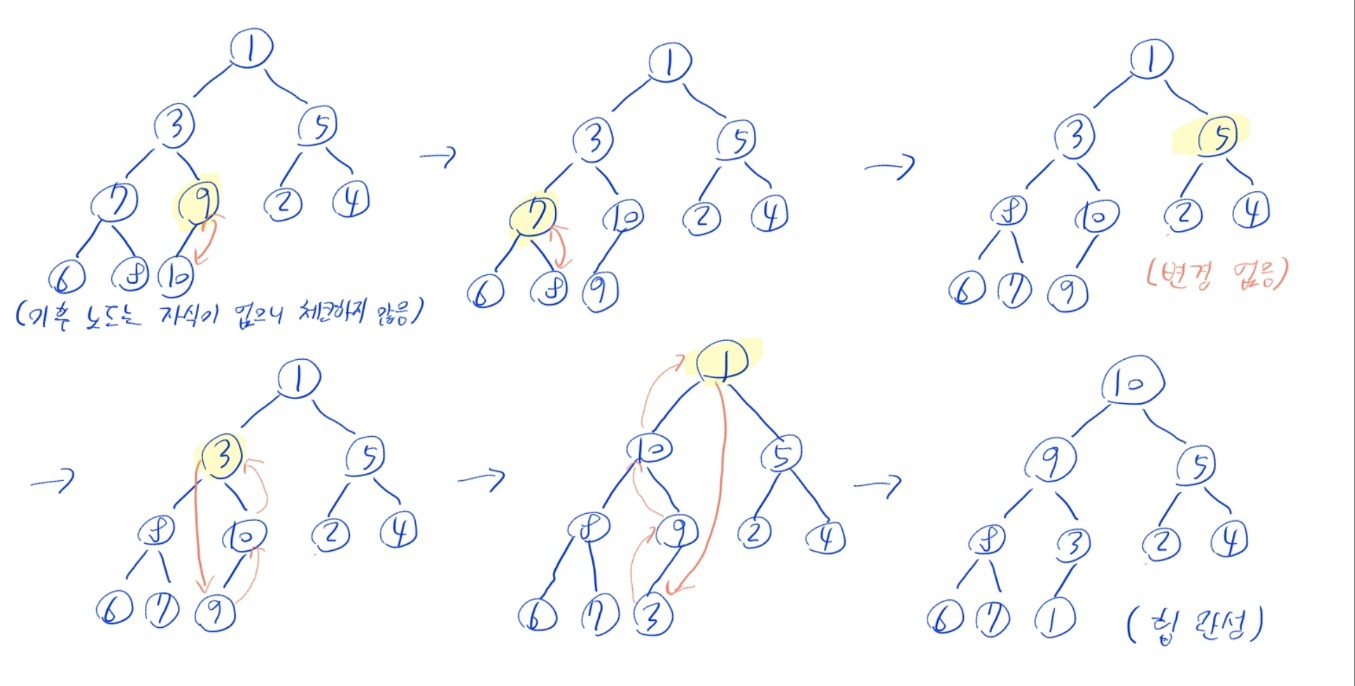
• 앞선 힙 정렬 알고리즘은, 힙의 성질을 만족하는 배열에서만 정상적으로 작동
• 따라서, 정렬할 배열을 미리 힙으로 만들어야 함
• (1) 자식이 있는 마지막 부모 노드부터, 배열의 원소를 역순으로 순회
  • n // 2 - 1 부터 역순으로 순회하면 됨
• (2) 현재 원소(노드)에서 시작하여, 자신보다 큰 값을 가진 자식과 자리를 바꾸며 아래로 내려가는 작업 반복
  • 힙의 재구성의 3단계 과정과 비슷하지만, 루트가 아닌 노드에서도 출발한다는 점이 다름
• (3) 위 과정을 모든 노드에 대해 실행

구현 과정

def heap_sort(a):

    # a[start] ~ a[end] 원소를 힙으로 만듦
    def down_heap(a, start, end):
        # a[start] 외엔 힙 상태로 가정
        # a[start] 를 알맞은 위치로 내려 힙 상태 만들기
        value = a[start]
        parent = start

        while True:
            cl = 2 * parent + 1     # 왼쪽 자식
            cr = cl + 1             # 오른쪽 자식

            # 자녀가 없는 경우 break
            if cl > end:
              break

            # 더 큰 자식 선택
            if cr <= end and a[cr] > a[cl]:
                child = cr
            else:
                child = cl

            # 부모가 두 자식보다 크거나 같으면 멈춤
            if value >= a[child]:
                break

            # 자식 값을 부모 위치로 끌어올림
            a[parent] = a[child]
            parent = child

        # value를 최종 위치에 저장
        a[parent] = value

    n = len(a)

    # 배열 a를 힙으로 만들기
    for i in range(n // 2 - 1, -1, -1):
        down_heap(a, i, n - 1)

    # 최댓값(루트)를 배열 끝으로 이동
    # 나머지 원소들을 힙으로 재구성
    # 위 과정을 반복
    for i in range(n - 1, 0, -1):
        a[0], a[i] = a[i], a[0]
        down_heap(a, 0, i - 1)

a = [6, 4, 3, 7, 1, 9, 8]
heap_sort(a)
print(a)

시공간 복잡도 및 안정성

시간 복잡도

• 배열의 원소 수를 $N$으로 두자
• down_heap로 노드를 힙 내 알맞은 위치로 내릴 때
  • 힙의 높이는 약 $log_2{N}$
  • 최악의 경우 루트에서 끝까지 내려가, $O(log N)$ 소요
• 배열을 힙으로 만들 때
  • 배열의 모든 원소에 대해 down_heap을 하면 $O(N log N)$ 같지만, 실제론 $O(N)$
  • 위쪽 노드는 적지만 이동 거리가 길고, 아래쪽 노드는 많지만 이동 깊이가 짧으므로 합은 $O(N)$으로 수렴
• 루트를 꺼내고, 나머지 원소들로 힙을 재구성할 때
  • 여기선 down_heap이 항상 루트부터 시작하므로, 이동 깊이는 $\log N$
  • down_heap을 $N-1$번 반복 -> $O(N log N)$
• 최종 $O(N \log N)$

공간 복잡도

• 배열 a의 원소의 교환만 이루어지고, 추가 배열이 선언되지 않음
• 재귀 역시 사용되지 않음
• 최종 $O(1)$

안정성

• 떨어져 있는 원소의 교환이 이루어지므로, 안정적이지 않음

도수 정렬

• 두 원소의 값을 비교하지 않음
• 대신 각 원소가 몇 개 존재하는지 개수를 셈

• 실수: 누적도수분포표의 8, 9번 인덱스는 0이 아니라 8입니다.
• 실수: 최종 정렬 결과는 [0, 1, 2, 3, 3, 4, 5, 7, 10]입니다.

과정

• (1) 도수분포표 배열 freq을 만듦
  • freq[x]는 원소 x가 몇 개인지 나타냄
  • e.g., 배열이 0~10의 자연소 원소로 구성된 경우, 원소를 총 11개로 구성
• (2) freq[x]를 값 x 이하인 원소 개수로 업데이트
• (3) 정렬할 배열과 동일 길이의 배열 output을 만듦
• (4) a를 역순으로 순회하며, 아래와 같이 output에 저장

for i in range(n - 1, -1, -1):
  # 현재 값의 인덱스 구하기
  freq[a[i]] -= 1
  # 해당 인덱스에 넣기
  output[freq[a[i]]] = a[i]

def counting_sort(a):
    max_elem = max(a)
    n = len(a)

    freq = [0] * (max_elem + 1) # 도수분포표 배열
    output = [0] * n            # 정렬 결과

    # 원소별 개수 계산
    for i in range(n):
        freq[a[i]] += 1

    # 누적도수분포 계산
    for i in range(1, len(freq)):
        freq[i] += freq[i - 1]

    # 정렬
    for i in range(n - 1, -1, -1):
        freq[a[i]] -= 1
        output[freq[a[i]]] = a[i]

    for i in range(n):
        a[i] = output[i]

a = [5, 7, 0, 2, 4, 10, 3, 1, 3] # [0, 1, 2, 3, 3, 4, 5, 7, 10]
counting_sort(a)
print(a)

시공간 복잡도 및 안정성

• 시간 복잡도: 배열의 원소 수를 $N$, 도수분포표의 값의 범위를 $K$로 둘 때, $O(N + K)$
  • 제한된 범위 내 중복되는 값이 많은 경우 효과적
  • 값의 범위가 넓을수록 비효율적
• 공간 복잡도: 도수분포를 저장하기 위해 $O(K)$, 결과값을 저장하기 위해 $O(N)$ -> $O(N + K)$
• 역순으로 순회하는 이유: 동일한 값의 원소의 순서를 유지하기 위해 (안정성 유지)

.sort(), sorted()

• 병합 정렬과 삽입 정렬을 혼합한 알고리즘을 사용한다고 함
• 평균적으로 $O(N \text{log} N)$, 알고리즘 문제 풀이 시 이를 기준으로 계산하기

문제풀이

2751. 수 정렬하기 2

백준 / 실버 5 / 2751. 수 정렬하기 2

• 최대 $1,000,000$개의 수를 정렬해야 함
  • $O(N log N)$을 보장하는 알고리즘이 필요함
• 내가 풀었을 때, 퀵 정렬로는 시간초과 뜨고, 병합 정렬로는 시간 내에 풀 수 있었음
  • 추측하건대 퀵 정렬은 배열이 균등하게 나뉘지 않는 경우 $O(N^2)$까지 시간 복잡도가 올라가서 그런 것 같음
• 그리고 이런 입력값 많이 받는 문제는 sys.stdin.readline 써야 함!!!

import sys
input = sys.stdin.readline

def merge_sort(a, start, end):
    if start < end:
        mid = (start + end) // 2
        merge_sort(a, start, mid)
        merge_sort(a, mid + 1, end)

        i = start
        j = mid + 1
        merged = []

        while i <= mid and j <= end:
            if a[i] <= a[j]:
                merged.append(a[i])
                i += 1
            else:
                merged.append(a[j])
                j += 1

        while i <= mid:
            merged.append(a[i])
            i += 1

        while j <= end:
            merged.append(a[j])
            j += 1

        for i in range(len(merged)):
            a[start + i] = merged[i]

N = int(input())
nums = []
for _ in range(N):
    nums.append(int(input()))

merge_sort(nums, 0, len(nums) - 1)

for n in nums:
    print(n)

10989. 수 정렬하기 3

백준 / 브론즈 1 / 10989. 수 정렬하기 3

• 최대 $10,000,000$개의 수를 정렬해야 함
  • $O(N)$ 아니면 시간초과... 병합 정렬도 어려움
• 하지만 $10,000$보다 작거나 같은 자연수만 원소로 주어짐
  • 범위가 제한되어 있으면 도수 정렬이 효과적

import sys
input = sys.stdin.readline

N = int(input())
count = [0] * 10001

# O(N)
for _ in range(N):
    num = int(input())
    count[num] += 1

# O(K)
for i in range(1, len(count)):
    for _ in range(count[i]):
        print(i)

• 위 코드로 $O(N + K)$, 즉 최대 $10,010,000$회 연산으로 문제를 풀 수 있음
• 정렬된 배열을 구하는 문제가 아니라 정렬 결과를 출력하는 문제이므로, 단순히 원소별 개수를 계산하고, 작은 원소부터 출력하면 됨

1181. 단어 정렬

백준 / 실버 5 / 1181. 단어 정렬

• 본 문제에선 $N$개의 단어를 길이가 짧은 순, 길이가 같으면 사전 순으로 정렬해야 함
  • .sort()나 sorted()의 key 매개변수에 정렬 기준을 반환하는 함수를 입력할 수 있음
  • 정렬 기준이 2개 이상인 경우, 각 기준을 담은 튜플을 반환하게 함
• 중복된 단어는 1개만 남기고 제거해야 함
  • 중복을 허용하지 않는 집합 자료형에 단어를 추가
  • 단 집합은 순서를 허용하지 않으므로, 정렬 전에 리스트로 바꿔 주어야 함

N = int(input())
words = set([]) # 집합은 중복을 허용하지 않음

for _ in range(N):
    words.add(input())

words = list(words) # 정렬을 위해 리스트로 변경
# 순서: 길이 -> 사전순
words.sort(key=lambda x: (len(x), x))

for w in words:
    print(w)

20920. 영단어 암기는 괴로워

[백준 / 실버 3 / 20920. 영단어 암기는 괴로워]

• 단어 등장 횟수를 내림차순 -> 단어 길이를 내림차순 -> 사전 순으로 정렬해야 함
• 정렬 기준이 여러 개이므로, 앞선 단어 정렬 문제처럼 튜플을 반환하는 함수를 인수 key로 보내야 함
  • 이때 내림차순인 경우 값을 음수 처리하면 됨

from collections import Counter

N, M = map(int, input().split())
words = []

# 단어 리스트
for _ in range(N):
    word = input()
    if len(word) < M:
        continue
    words.append(word)

# 단어의 수 세기: 각 단어의 등장 수를 저장한 딕셔너리 반환
words_count = Counter(words)

# 중복 단어 제거
words = list(set(words))

# 정렬: 자주 나오는 순서 -> 단어의 길이 -> 알파벳 사전순
# 역순은 - 붙이기
words.sort(key=lambda x: (-words_count[x], -len(x), x))

for word in words:
    print(word)

18870. 좌표 압축

백준 / 실버 2 / 18870. 좌표 압축

• $X_i$를 좌표 압축한 결과 $X'_i$의 값은 $X_i > X_j$를 만족하는 서로 다른 좌표 $X_j$의 개수여야 함
  • $X_i > X_j$ 만족 원속 수: 정렬된 리스트의 인덱스는, 해당 값보다 작은 원소의 개수와 동일
  • 서로 다른 좌표: 집합 자료형을 사용해서 중복값을 없앰
  • 입력값 배열을 집합으로 만든 뒤, 다시 리스트로 만들어 정렬하기
• e.g., [2, 4, -10, 4, 9] -> {2, 4, -10, 9} -> [-10, 2, 4, 9]
  • 9보다 작은 좌표는 -10, 2, 4 3개
  • 정렬된 리스트에서 9는 3번째 인덱스에 위치

N = int(input())
array = list(map(int, input().split()))

# 집합으로 중복값 없애고, 다시 리스트로 변환 후 정렬
set_array = list(set(array))
set_array.sort()

# 각 좌표의 인덱스 저장
x_dict = dict()
for i in range(len(set_array)):
    x_dict[set_array[i]] = i

# 압축된 좌표 반환
for a in array:
    print(x_dict[a], end=" ")

• 시간 복잡도: 정렬 과정에서 $O(N \log N)$ -> $O(N \log N)$