백준 막 입문했을 때 재귀함수가 뭔지도 모르고 N-Queen 문제를 풀려고 했다가 3시간 넘게 삽질했던 기억이 난다. 다행히 이번 기회에 완전히 이해한 것 같다. 아마도...?

재귀 알고리즘

• 재귀적 정의: 어떤 개념이나 함수를 자기 자신을 참조하여 정의하는 방식
• 재귀 호출: 자기 자신과 똑같은 함수를 호출하는 것
• 재귀 알고리즘은 무조건 종료 조건이 존재해야 함
  • 종료 조건에선 추가로 재귀 호출을 하지 않음
  • 종료 조건이 없으면 재귀 호출이 계속 반복되어 무한 재귀 상태가 됨

유클리드 호제법

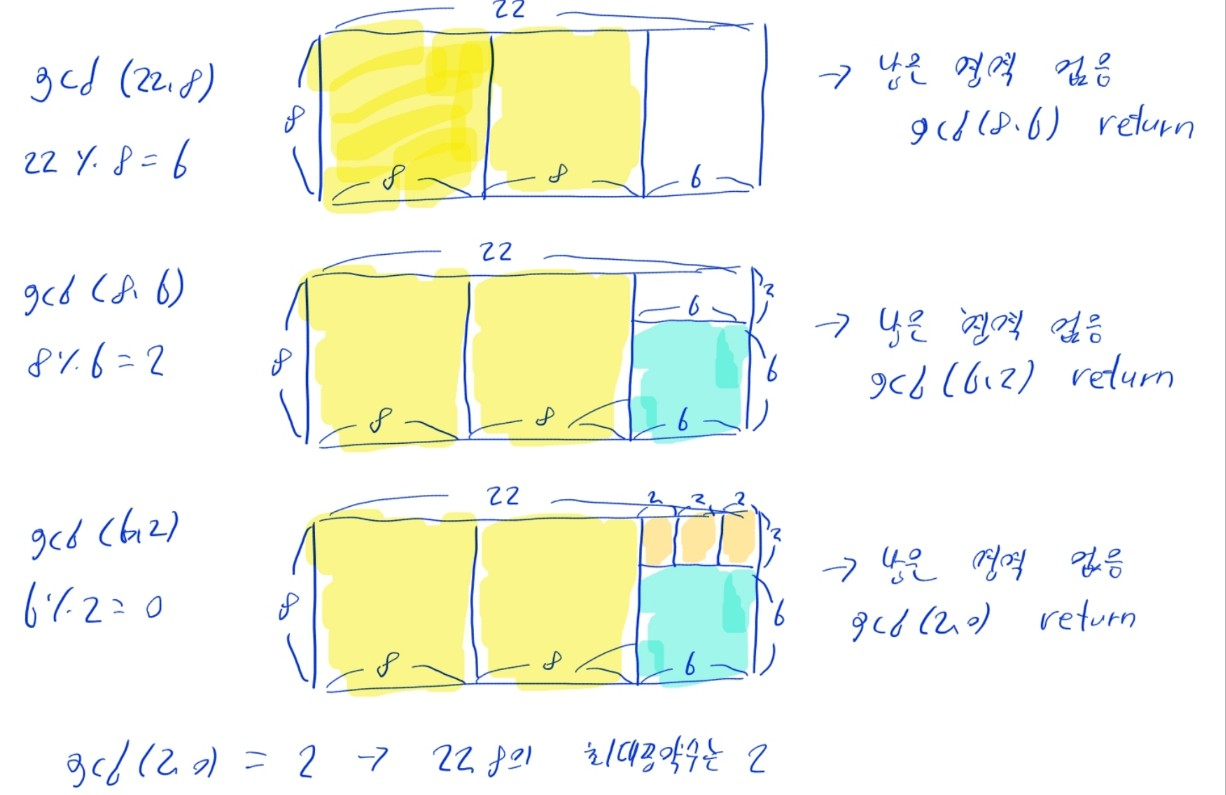
• 두 정숫값의 최대 공약수 구하기
• 두 정수 $x, y$의 최대 공약수를 $\text{gcd}(x, y)$로 둘 때
  • $y$가 $0$이면 $x$ (종료 조건)
  • $y$가 $0$이 아니면 $\text{gcd}(y, x \% y)$
• 직사각형 안을 정사각형 여러 개로 채울 때, 만들 수 있는 정사각형 가운데 가장 작은 정사각형의 변의 길이를 구하는 문제로 이해하면 됨

def gcd(x, y):
    if y == 0:
        return x
    else:
        return gcd(y, x % y)

print(gcd(22, 8))   # 2

• gcd(22, 8) 실행 -> gcd(8, 6) 재귀호출
• gcd(8, 6) 실행 -> gcd(6, 2) 재귀호출
• gcd(6, 2) 실행 -> gcd(2, 0) 재귀호출
• gcd(2, 0) 실행 -> 2 반환
• 앞선 함수들도 재귀적으로 2를 반환

재귀 알고리즘 분석

def recur(n):
    if n > 0:
        recur(n - 1)
        print(n, end=" ")
        recur(n - 2)

recur(4)    # 1 2 3 1 4 1 2

• 종료 조건: n <= 0

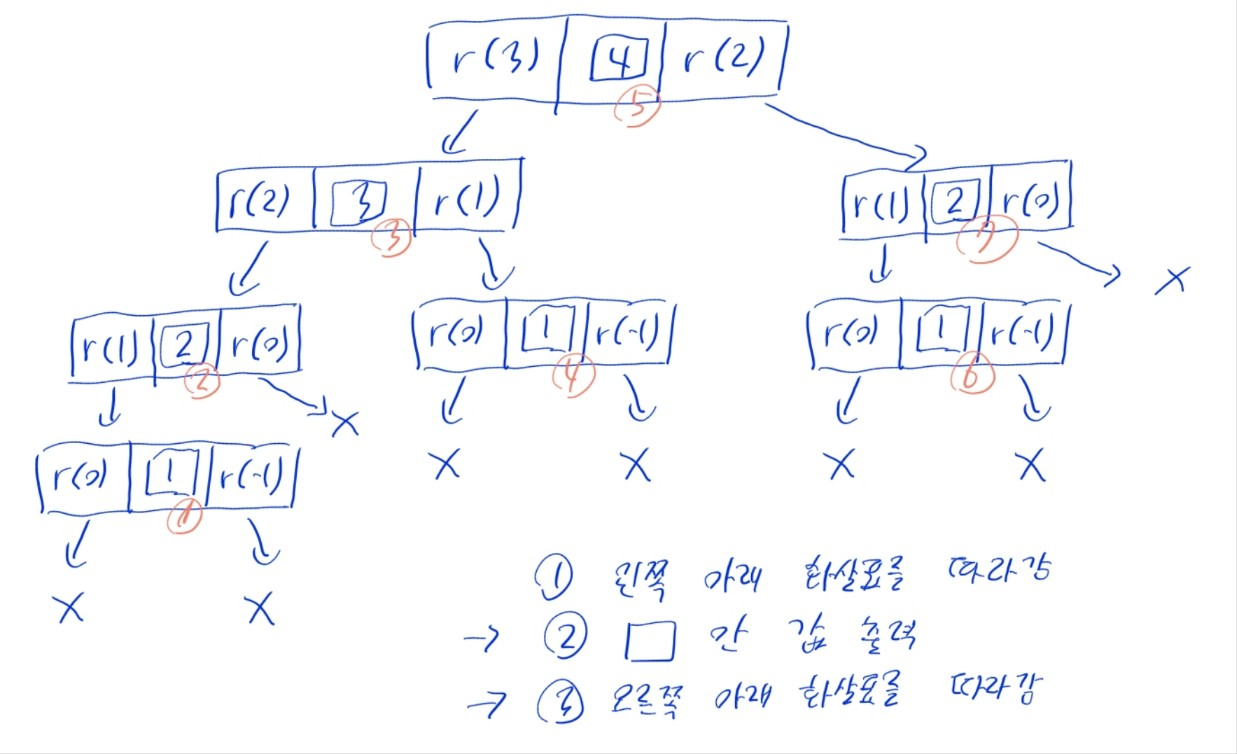
하향식 분석

• 제일 먼저 호출된 recur(4)부터 분석
• 다만, 같은 함수를 여러 번 호출하게 되므로 반드시 효율적이라고 할 수 없음

상향식 분석

• 하향식 분석과는 반대로, 아래쪽부터 쌓아 올리며 분석
• $n > 0$일 때만 실행하므로, recur(1)부터 분석
• 재귀함수 호출 시, 앞서 이미 구했던 결과를 그대로 사용

스택을 사용한 비재귀적 표현

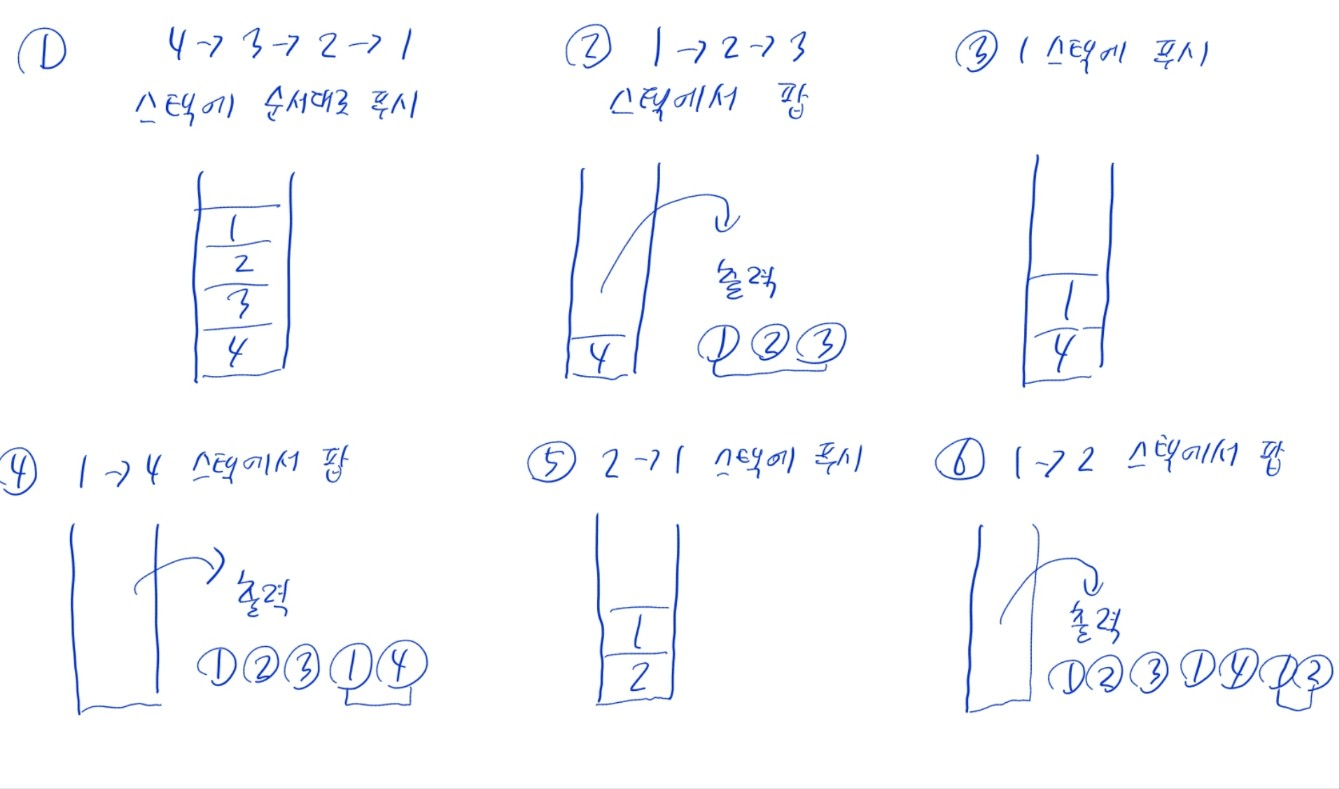
• recur()에선 n을 출력하기 전 recur(n - 1)을 실행해야 함
• 이때 recur(n-1)의 처리가 마무리될 때까지 n을 어딘가에 저장해야 함 -> 스택!

def recur(n):
    stack = []
    while True:
        if n > 0:
            stack.append(n)
            n -= 1
            continue
        elif len(stack) != 0:
            n = stack.pop()
            print(n, end = " ")
            n -= 2
            continue
        break

recur(4)    # 1 2 3 1 4 1 2

• n을 스택에 쌓고 n -= 1로 값을 변경
  • recur(n-1) 호출과 같음
• n <= 0일 때 스택에서 값을 꺼내 n에 저장 및 출력하고, n -= 2로 값을 변경
  • print(n) 후 recur(n-2) 호출과 같음

재귀 vs 반복문

• 위 예제의 경우 기존 재귀 문제를 반복문으로 구현해서 해결함
• 두 방법은 각자 장단점이 있음

	장점	단점
재귀	문제를 보다 직관적이고 간결한 코드로 표현 가능 특히 하노이의 탑 등 분할정복 문제에 적합	너무 많은 재귀 호출 -> 스택 오버플로우 발생 가능
반복문	일반적으로 성능이 더 빠르며, 메모리 사용량이 더 적음	문제 코드가 덜 직관적

• 스택 오버플로우
  • 함수를 호출할 때마다 컴퓨터는 함수 실행에 필요한 정보를 저장해야 함
  • 매개변수, 함수의 지역 변수, 반환 값 등 정보를 스택 프레임이라 부름
  • 재귀 함수가 호출될 때마다 스택 프레임이 콜 스택에 쌓임 (실행이 완료되면 스택에서 빠짐)
  • 재귀 호출이 너무 깊어 콜 스택 공간을 초과하는 경우, 스택 오버플로우가 발생

• 최대 재귀 깊이, 즉 한 번에 실행 중인 재귀 함수의 최대값만큼의 메모리가 필요함
  • 재귀함수의 총 실행 횟수가 아닌, 한 번에 실행 중인 함수 횟수의 최대값임에 유의할 것
  • e.g., 퀵 정렬의 공간 복잡도, 병합 정렬의 공간 복잡도

• 반복문의 성능이 더 좋은 이유
  • 반복문은 함수 호출 없이 순서대로 작업을 반복, 매번 함수 정보를 따로 저장할 필요 X
  • 즉 실행 속도도 빠르며, 메모리 사용량도 더 적음
• 그럼에도 불구하고, 몇몇 문제들은 재귀로 코드를 구현하는 것이 훨씬 직관적
  • 특히 전체 문제를 부분 문제로 나눠 생각해야 하는 문제 (하노이의 탑)
  • 특히 분기를 나눠 경우의 수를 따져보는 문제 (N-Queen)

하노이의 탑

• 3개의 기둥 -> 왼쪽 기둥에서 오른쪽 기둥으로 원반을 모두 옮기는 문제
• 단 작은 원반이 위에, 큰 원반이 아래에 위치하는 규칙을 지켜야 함

재귀적 분석

• 상향식으로 원반이 1개일 때부터 생각해보자
• 한 기둥에서 다른 기둥으로 모든 원반을 옮기는 데, 몇 회가 소요될까?
• 시작 기둥을 A, 중간 기둥을 B, 도착 기둥을 C이라 두자

• 원반이 1개일 때
  • 원반 1을 A -> C로 이동
  • 총 1회

• 원반이 2개일 때
  • 원반 1을 A -> B로 이동
  • 원반 2를 A -> C로 이동
  • 원반 1을 B -> C로 이동
  • 총 3회

• 원반이 3개일 때
  • 원반 1, 2를 그룹으로 생각하기
  • 원반 1+2를 A -> B로 이동 (3회)
  • 원반 3을 A -> C로 이동
  • 원반 1+2를 B -> C로 이동 (3회)
  • 총 7회

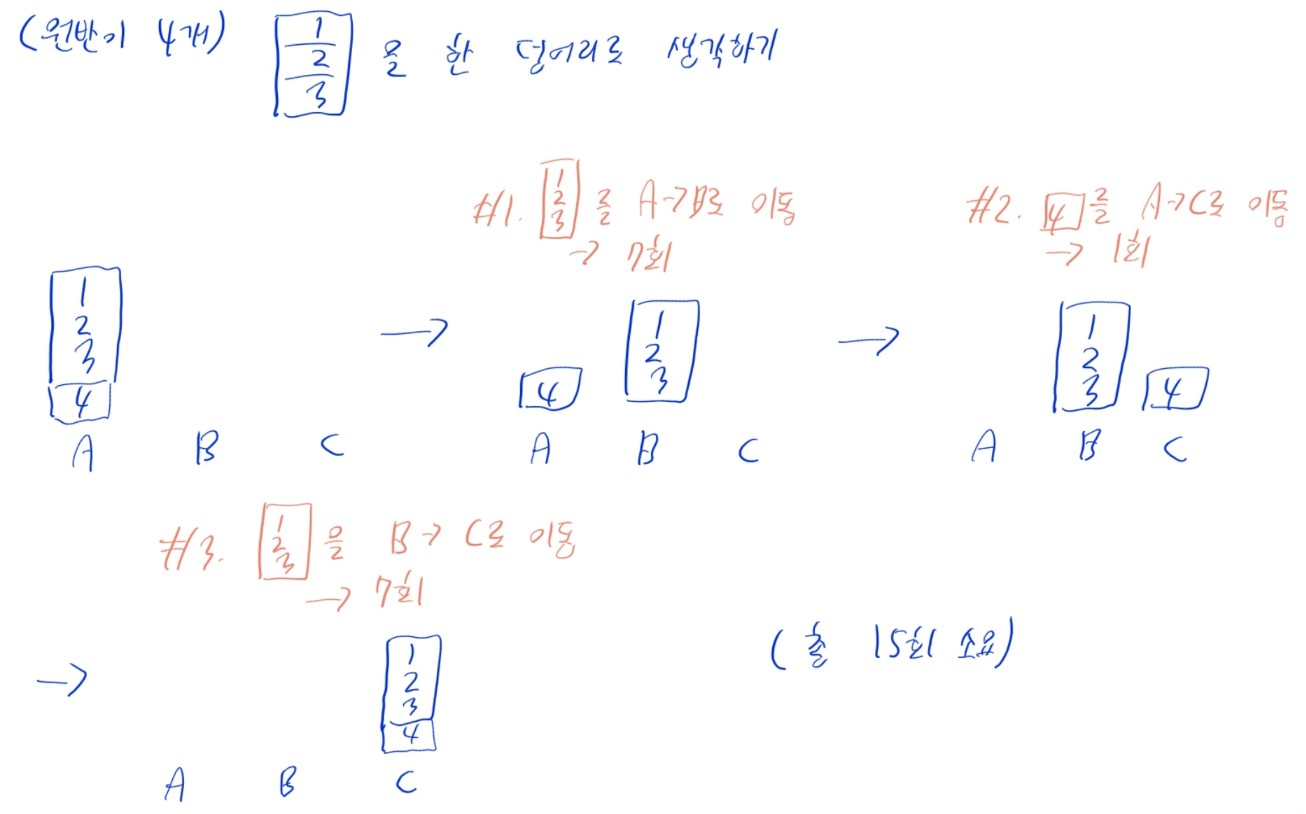
• 원반이 4개일 때
  • 원반 1, 2, 3을 그룹으로 생각하기
  • 원반 1+2+3을 A -> B로 이동 (7회)
  • 원반 4를 A -> C로 이동
  • 원반 1+2+3을 B -> C로 이동 (7회)
  • 총 15회

• 즉, 원판 $N$개를 한 기둥에서 다른 기둥으로 옮길 때 필요한 횟수를 $\text{move}(N)$으로 둘 때
  • $\text{move}(1) = 1$
  • $\text{move(N)} = \text{move(N - 1)} + 1 + \text{move(N - 1)}$

구현

count = 0

# 원판 num개를 x기둥 -> y기둥으로 이동
def move(num, x, y):
    global count

    if num > 1:
        move(num - 1, x, 6 - x - y)

    count += 1
    print(f"#{count:0>2}: 원반 {num}를 기둥 {x}->{y}로 이동")

    if num > 1:
        move(num - 1, 6 - x - y, y)

# 첫 기둥에 쌓인 원판 4개를 세번째 기둥으로 옮김
move(4, 1, 3)

#01: 원반 1를 기둥 1->2로 이동
#02: 원반 2를 기둥 1->3로 이동
#03: 원반 1를 기둥 2->3로 이동
#04: 원반 3를 기둥 1->2로 이동
#05: 원반 1를 기둥 3->1로 이동
#06: 원반 2를 기둥 3->2로 이동
#07: 원반 1를 기둥 1->2로 이동
#08: 원반 4를 기둥 1->3로 이동
#09: 원반 1를 기둥 2->3로 이동
#10: 원반 2를 기둥 2->1로 이동
#11: 원반 1를 기둥 3->1로 이동
#12: 원반 3를 기둥 2->3로 이동
#13: 원반 1를 기둥 1->2로 이동
#14: 원반 2를 기둥 1->3로 이동
#15: 원반 1를 기둥 2->3로 이동

• 종료 조건: num == 1

N-queen 문제

• N개의 퀸이 서로 공격하여 잡을 수 없도록 NxN 체스판에 배치하는 문제
• 퀸은 체스판의 가로, 세로, 대각선의 8가지 방향으로 직선 이동하여 상대방을 잡을 수 있음

분기 한정법

• $N^2$개의 칸에 $N$개의 말을 두는 경우의 수 -> 많다.
  • $N = 8$일 때, $\binom{64}{8} = \frac{64!}{56!8!} =$ 약 44억
  • 일일이 확인하는 것보다 빠른 방법을 찾아야 함
• 모든 경우를 나열하기보단, 가능한 경우만 탐색하여 시간을 줄이는 것이 중요
• 분기 한정법을 쓰는 것이 효과적
  • 분기: 가능한 선택지를 하나씩 시도하는 것
  • 한정: 가능하지 않은 선택지를 미리 잘라내는 것

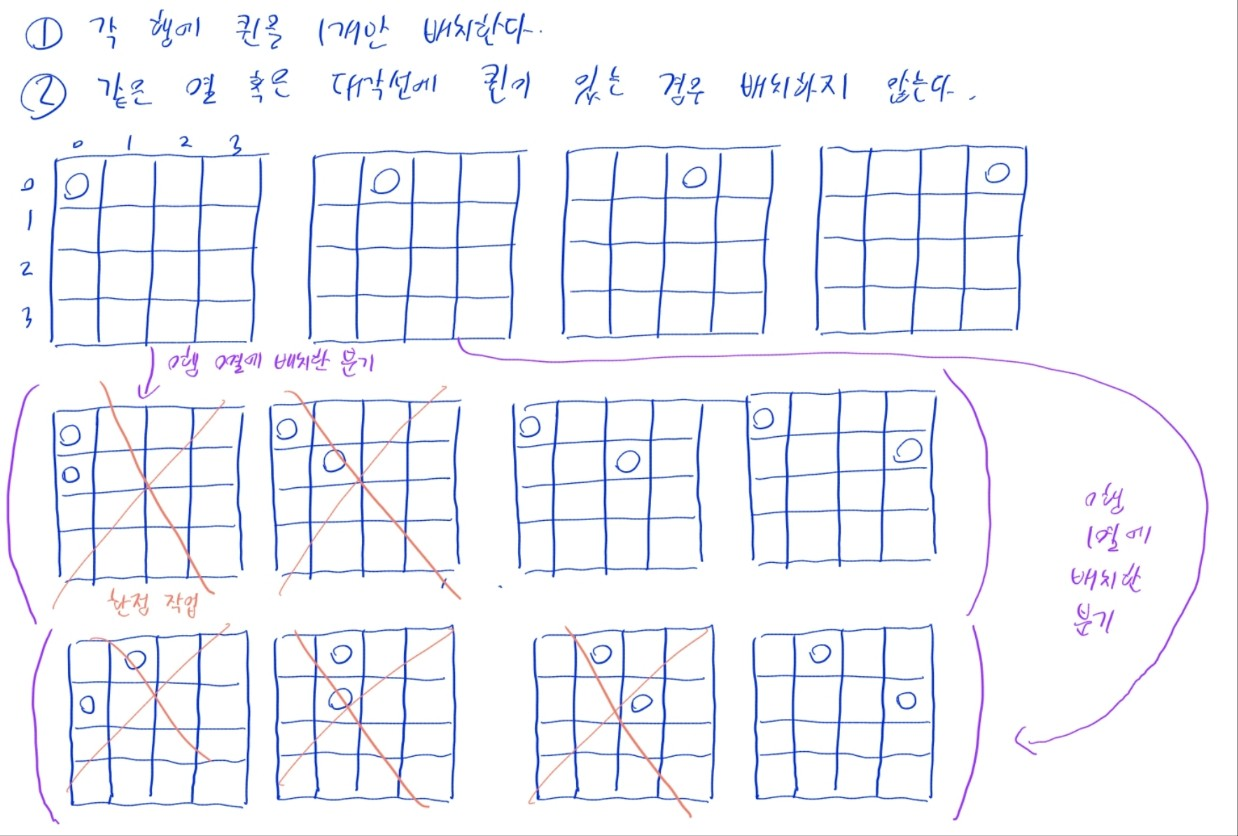
• 각 행에 퀸을 하나씩 배치한다는 기본 조건을 바탕으로, 퀸을 배치하기
• (1) 0행부터 시작하여, 각 열 위치에 퀸을 둘 수 있는지 하나씩 시도 (분기 작업)
• (2a) 퀸을 둘 수 있는 경우, 다음 행으로 넘어가 계속해서 배치 시도
• (2b) 같은 열 또는 대각선에 퀸이 있는 경우, 해당 열 위치는 건너뜀 (한정 작업)
• (3) 0행부터 $N-1$행까지 모두 퀸을 배치한 경우, 하나의 정답으로 간주해 출력

def n_queen(n):
    rows = [0] * n                      # 각 행에서 퀸의 위치
    cols = [False] * n                  # 각 열의 퀸 배치 여부
    diag_a = [False] * (2 * n - 1)      # ↖↘ 대각선에서의 퀸 배치 여부
    diag_b = [False] * (2 * n - 1)      # ↙↗ 대각선에서의 퀸 배치 여부

    def show():
        for p in rows:
            print(f"{p:2}", end=" ")
        print()

    def place(i):                       # i행에 퀸을 배치
        if i >= n:                      # 모든 행에 다 채운 경우 출력
            show()
        else:
            for j in range(n):
                if (not cols[j] and not diag_a[i - j + n - 1] and not diag_b[i + j]):
                    # 동일 열 및 대각선에 퀸이 없는 경우, i행 j열에 배치
                    rows[i] = j
                    cols[j] = diag_a[i - j + n - 1] = diag_b[i + j] = True
                    place(i + 1)    # 다음 행으로 이동
                    # 퀸을 j열에서 제거
                    cols[j] = diag_a[i - j + n - 1] = diag_b[i + j] = False

    place(0)

n_queen(8)

• 종료 조건: i >= n

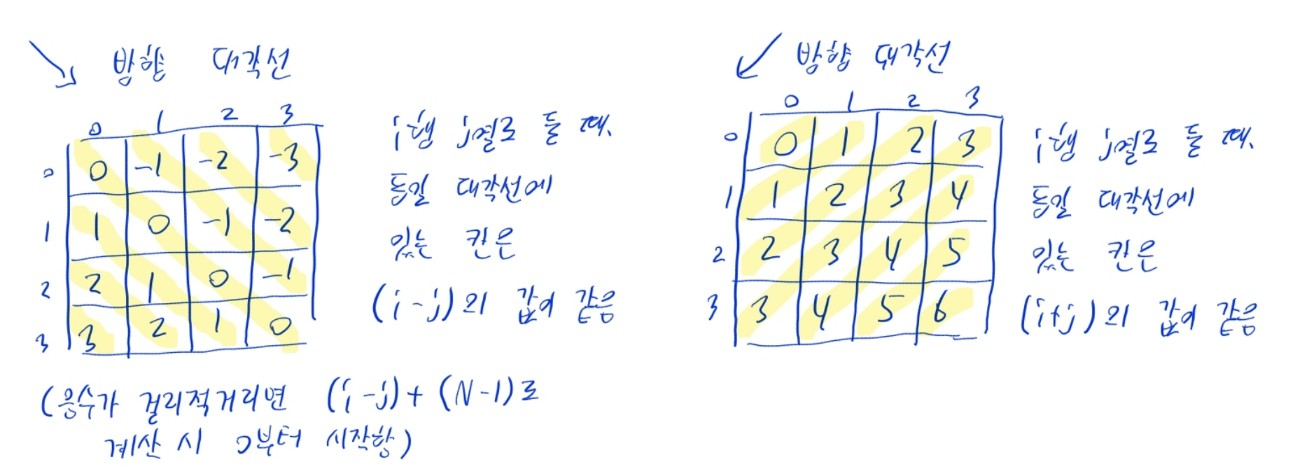
대각선 열을 체크하는 방법

• 행과 열 인덱스의 합과 차로 구분

문제풀이

1074. Z

풀이가 길어져 링크로 대체

9663. N-Queen

백준 / 골드 4 / 9663. N-Queen

• 위의 N-Queen 구현 예제와 비슷하지만, 각 배치를 출력하는 게 아니라, 모든 가능한 배치의 경우의 수를 계산한다는 차이가 있음
• i >= N으로 모든 행에 퀸을 배치했을 경우, 하나의 경우이므로 1을 반환
• 다른 경우, count 변수에 place_row를 호출하며 얻은 반환값을 누적해서 더해 반환
• 최종적으로는 가능한 조합 수를 반환하게 됨

N = int(input())

cols = [False] * N              # 열 정보
diag_a = [False] * (2 * N - 1)  # / 대각선 정보
diag_b = [False] * (2 * N - 1)  # \ 대각선 정보

def place_row(i):
    if i >= N:
        return 1

    count = 0
    for j in range(N):
        if (not cols[j] and not diag_a[i + j] and not diag_b[i - j + N - 1]):
            cols[j] = diag_a[i + j] = diag_b[i - j + N - 1] = True
            count += place_row(i + 1)
            cols[j] = diag_a[i + j] = diag_b[i - j + N - 1] = False
    return count

print(place_row(0))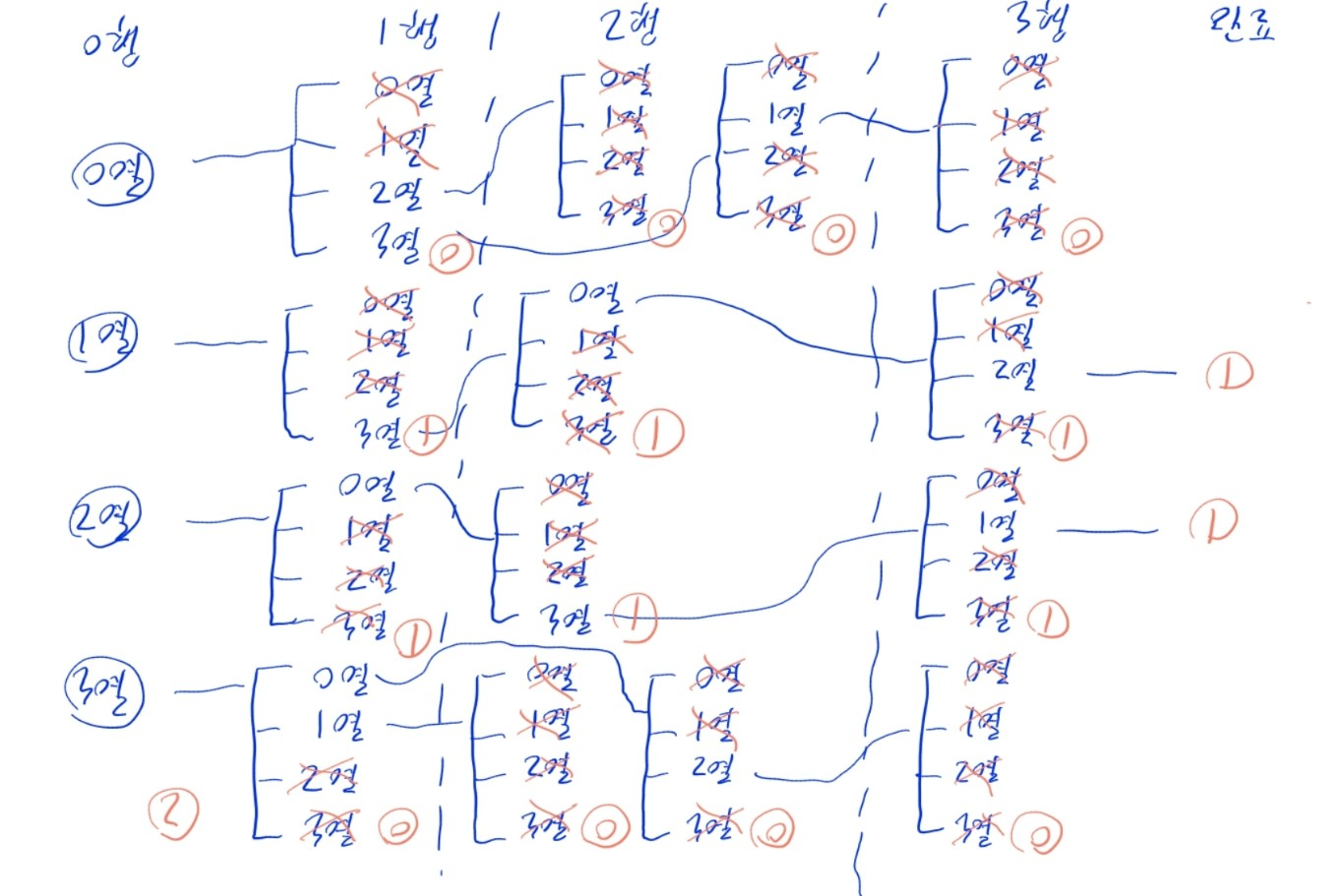

• 빨간 원으로 표시한 숫자가, 해당 분기의 함수가 return하는 값임.
• 시간 복잡도
  • 이론상 $O(N!)$지만, 실제로는 분기 한정법을 사용하여 탐색 공간을 줄이기 때문에 훨씬 짧게 걸림
  • 분기 한정법 문제의 정확한 시간 복잡도는 구하기 어려움
  • 탐색 공간이 조건에 따라 유동적으로 줄어들기 때문에, 평균 시간 분석이 복잡함