트리

• 한 점에서 시작해서, 나무처럼 갈라져 나가는 자료구조라고 생각하면 됩니다.

트리의 구조

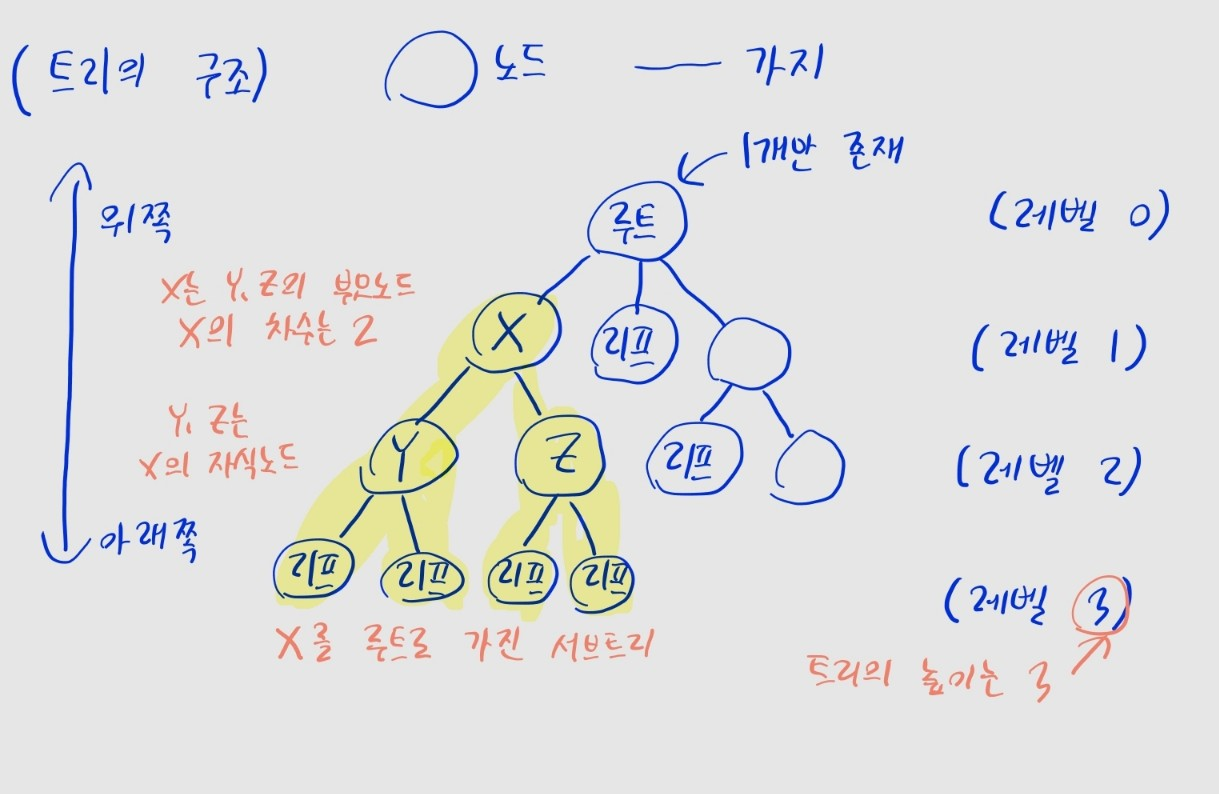
• 트리는 노드와 간선으로 구성됨
  • 노드: 데이터 값을 가지는 원소
  • 간선: 노드와 노드를 연결하는 선
• 루트 노드 (이하 루트): 트리의 가장 위쪽에 있는 노드로, 트리에 1개만 존재
• 노드와 가지가 연결되었을 때,
  • 부모 노드: 위쪽에 있는 노드
  • 자식 노드: 아래쪽에 있는 노드
• 리프 노드 (이하 리프): 자식 노드가 없는 노드
• 서브트리: 트리 내 어떤 노드를 루트로 하고, 그 자손으로 구성된 트리
  • 트리 자기 자신도 서브트리
• 노드의 레벨: 각 노드가 루트 노드까지 가는 데 거치는 간선 수
  • 루트 노드의 레벨은 0
• 트리의 높이: 트리 내 루트에서 가장 멀리 있는 리프까지의 거리
  • 레벨의 최댓값으로 구할 수 있음

🤔 리프는 트리의 가장 아래쪽 레벨에 있는 노드를 말하는 건가요?

• 그렇게 오해하기 쉬운데, 아닙니다. 자식이 없으면 어떤 레벨에 있든 무조건 리프입니다.
• 위 그림을 보면 레벨 1, 2, 3 어디에든 자식이 없는 노드는 리프임을 알 수 있습니다.

트리의 탐색

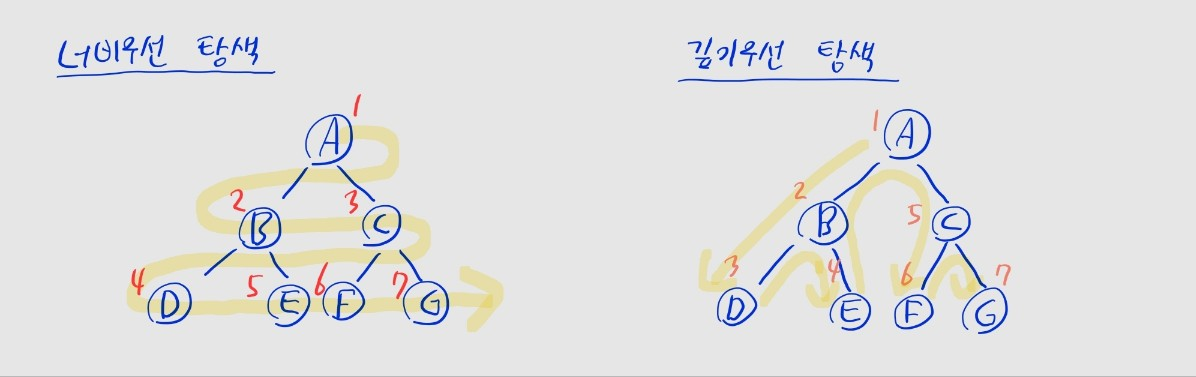
너비 우선 탐색 (BFS)

• 위쪽 레벨부터 왼쪽 -> 오른쪽으로 탐색
• 한 레벨에서 검색을 마치면, 다음 레벨로 내려감

깊이 우선 탐색 (DFS)

• 리프에 도달할 때까지 우선 아래쪽으로 내려감
  • 자식이 여러 개인 경우, 왼쪽 자식부터 탐색
• 리프에 도달해 더 이상 검색할 곳이 없으면, 일단 부모 노드로 돌아간 뒤 다음 자식 노드로 내려감

이진 트리

• $N$진 트리: 노드의 최대 차수가 $N$인 트리
  • 차수는 자식 수다... 기억하죠?
• 이진 트리: 모든 노드의 자식이 2개 이하인 트리
  • 자식이 하나만 있거나, 자식이 없는 노드가 존재해도 상관없음
  • 단 3개를 넘으면 안 됨
  • 왼쪽 자식, 오른쪽 자식을 구분함에 유의할 것

전위, 중위, 후위 순회

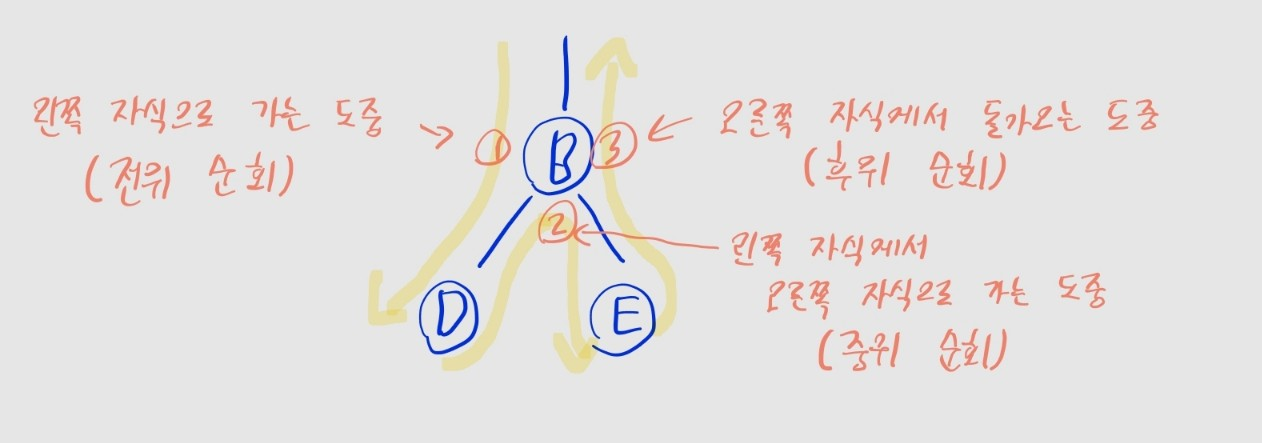
• 이진 트리의 깊이 우선 탐색에선, 한 노드를 최대 3번 지나가게 됨
  • (1) 왼쪽 자식으로 내려가는 도중
  • (2) 왼쪽에서 오른쪽 자식으로 이동하는 도중
  • (3) 오른쪽 자식에서 돌아오는 도중
• 이 중 언제 노드를 방문 처리하는지에 따라, 종류가 3개로 나뉨

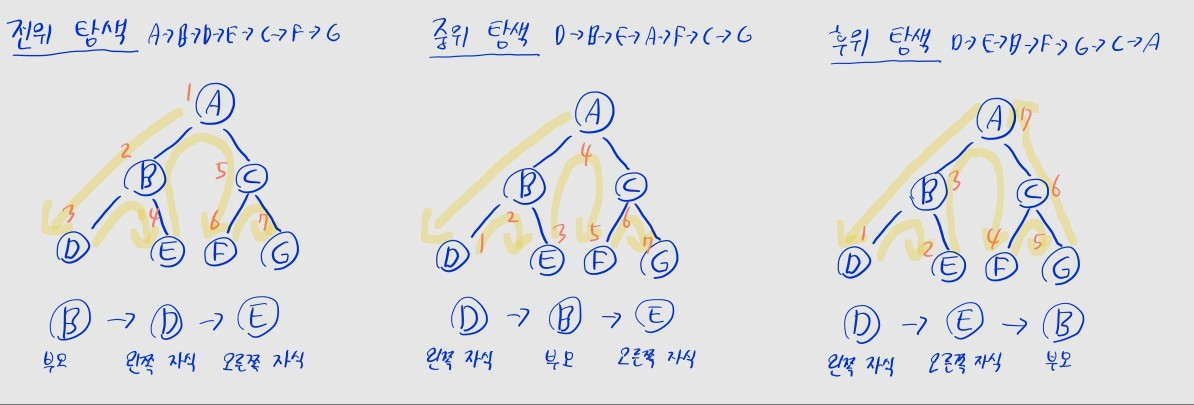
방법	탐색 순서
전위 순회	노드 방문 -> 왼쪽 자식 -> 오른쪽 자식
중위 순회	왼쪽 자식 -> 노드 방문 -> 오른쪽 자식
후위 순회	왼쪽 자식 -> 오른쪽 자식 -> 노드 방문

완전 이진 트리

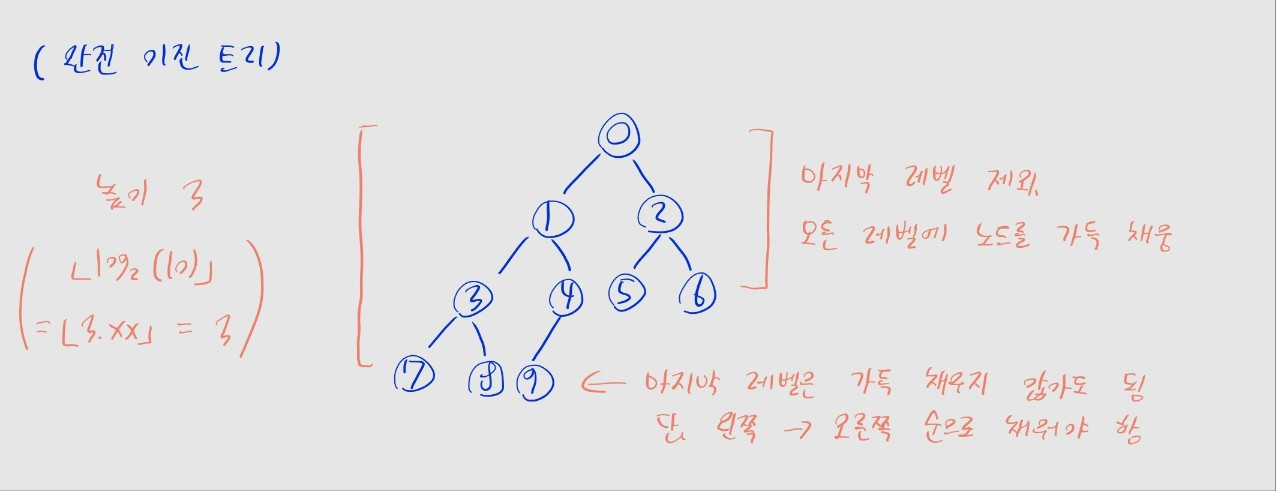
• 마지막 레벨을 제외하고, 모든 레벨에 노드가 가득 차 있음
• 마지막 레벨에 한해, 왼쪽부터 오른쪽으로 노드를 채우되, 반드시 끝까지 채우진 않아도 됨
• $N$개의 노드를 저장할 수 있는 이진 트리의 높이는 $\lfloor{\log_2 N}\rfloor$
  • e.g., 노드가 $10$개인 경우 $\lfloor{\log_2 10}\rfloor = \lfloor{3.\cdots}\rfloor = 3$, 높이 3
  • $\lfloor{x}\rfloor$는 $x$를 가장 가까운 정수로 내림
• 완전 이진 트리의 예시로, 최대 / 최소 힙이 있었음

이진 검색 트리

• 왼쪽 자식의 값이 자신의 값보다 작고
• 오른쪽 자식의 값이 자신의 값보다 큰 이진 트리

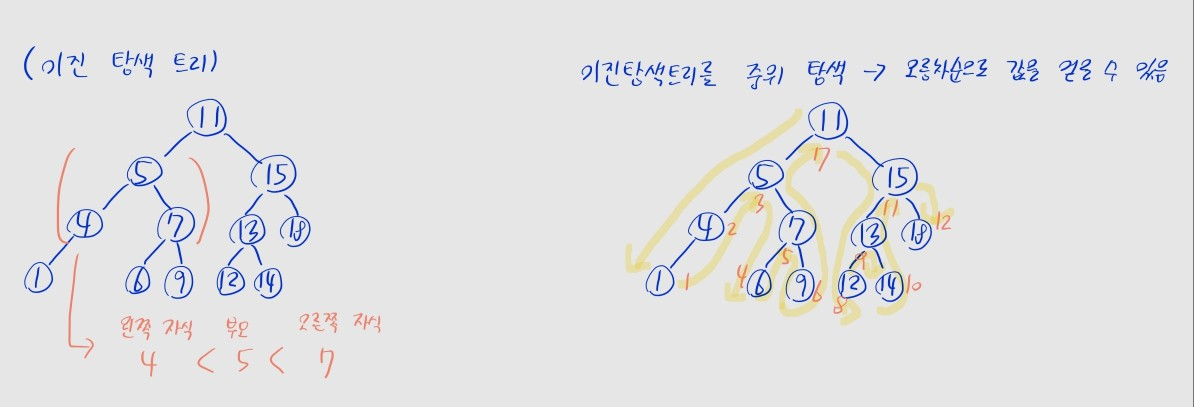
탐색이라 썼는데 뭐 같은 말입니다.

• 왼쪽으로만 이동하면 최솟값을, 오른쪽으로만 이동하면 최댓값을 얻을 수 있음
• 이진 검색 트리를 중위 순회하면, 값을 오름차순으로 방문할 수 있음

🤔 이진 검색 트리에는 동일한 값이 여러 개 존재할 수 있나요?

• 이진 검색 트리에는 중복된 값이 존재할 수 없습니다.
• 만약 중복되는 값을 다뤄야 한다면, 딕셔너리처럼 노드에 key와 value를 함께 저장하면 됩니다.
• 노드는 key의 순서 기준으로 배치하고, value로 중복 데이터를 관리하면 되겠죠.

이진 검색 트리 구현

• 일단 각 노드는 Node 클래스로 관리하겠습니다. 속성으로 왼쪽 자식 left, 오른쪽 자식 right, 값 key를 갖습니다.

class Node:
    def __init__(self, value):
        self.left = None
        self.right = None
        self.value = value

• 그리고 이진 검색 트리는 SearchTree 클래스로 관리하겠습니다. 일단 루트 노드만 속성 root로 지정하겠습니다.

class SearchTree:
    def __init__(self):
        self.root = None

값의 탐색

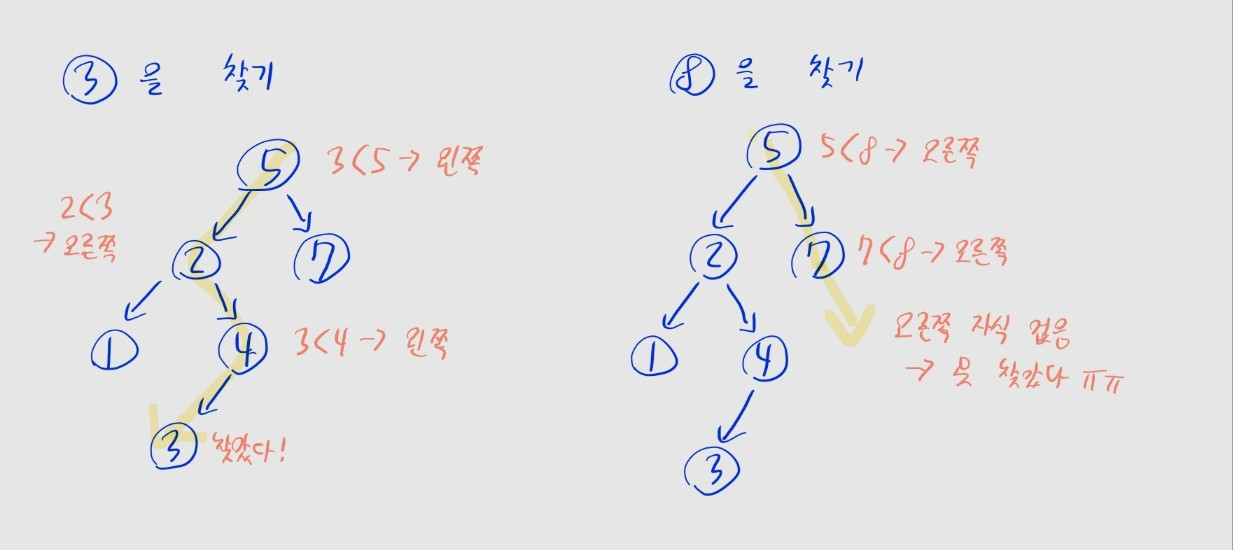
• 루트 노드부터 시작해서, 찾는 값과 노드의 값을 비교
• 찾는 값 < 노드 값인 경우, 왼쪽 자식 노드를 따라감
• 찾는 값 > 노드 값인 경우, 오른쪽 자식 노드를 따라감
• 해당 방향의 자식 노드가 존재하지 않는 경우, 탐색에 실패

# class SearchTree 계속
# 노드 검색
def search(self, target):
    curr = self.root    # 루트노드 부터 시작
    while curr:
        if curr.value == target:
            return True
        elif target < curr.value:
            curr = curr.left    # 왼쪽을 따라감
        elif curr.value < target:
            curr = curr.right   # 오른쪽을 따라감
    return False    # 탐색 실패

노드의 삽입

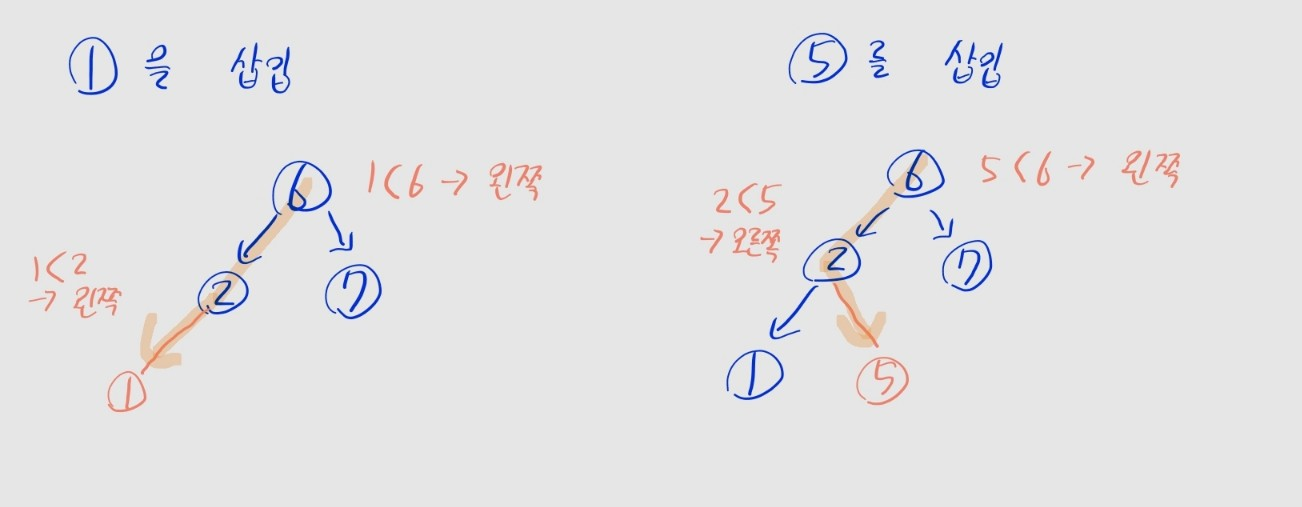
• 이진 검색 트리의 조건을 만족하는 위치에 삽입해야 함
• 따라서, 위 값의 탐색과 같은 방식으로 삽입할 위치를 찾아 삽입

# class SearchTree 계속
def insert(self, target):
    # 루트노드가 없을 때
    if self.root is None:
        self.root = Node(target)
    else:
        curr = self.root
        while True:
            # 왼쪽자식 추가
            if target < curr.value:
                if curr.left is None:
                    curr.left = Node(target)
                    break
                curr = curr.left

            # 오른쪽자식 추가
            if curr.value < target:
                if curr.right is None:
                    curr.right = Node(target)
                    break
                curr = curr.right
            
            # 동일 값 존재 시 추가 불가
            if curr.value == target:
                break

전위, 중위, 후위 순회

• 전위, 중위, 후위 순회를 하는 코드도 구현해보겠습니다.
• 현재 노드를 방문할 때 node.value를 출력
• 왼쪽 자식, 오른쪽 노드로 이동 시 재귀함수 호출
• 즉 재귀호출과 출력 순서를 잘 조절하는 게 중요해요.

# class SearchTree 계속
# 전위 순회: 루트 -> 현재 -> 오른쪽
def preorder(self, node):
    if node:
        print(node.value, end=' ')
        self.preorder(node.left)
        self.preorder(node.right)

# 중위 순회: 왼쪽 -> 현재 -> 오른쪽
def inorder(self, node):
    if node:
        self.inorder(node.left)
        print(node.value, end=' ')
        self.inorder(node.right)

# 후위 순회: 왼쪽 -> 오른쪽 -> 현재
def postorder(self, node):
    if node:
        self.postorder(node.left)
        self.postorder(node.right)
        print(node.value, end=' ')

노드의 삭제

삭제는 구현은 안 하겠습니다. 좀 많이 복잡해서 ㅠㅠ

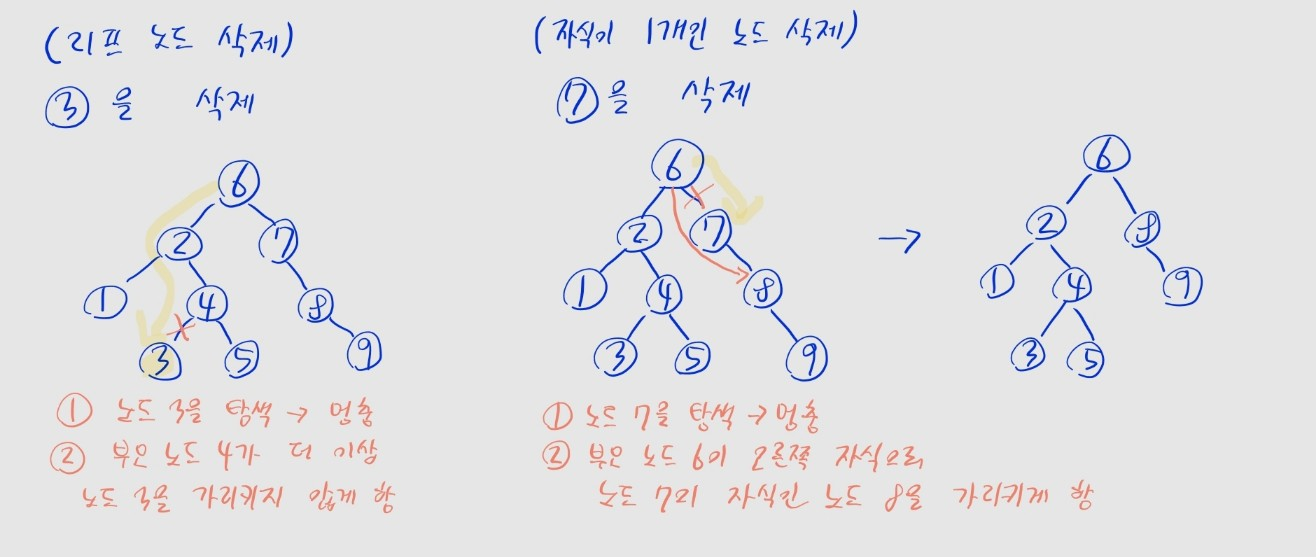
리프 노드일 때

• (1) 삭제할 노드까지 탐색
• (2) 부모 노드가 삭제할 노드를 가리키지 않도록 업데이트

자식이 1개인 노드일 때

• (1) 삭제할 노드까지 탐색
• (2) 부모 노드가 삭제할 노드의 자식을 가리키도록 업데이트

자식이 2개인 노드일 때

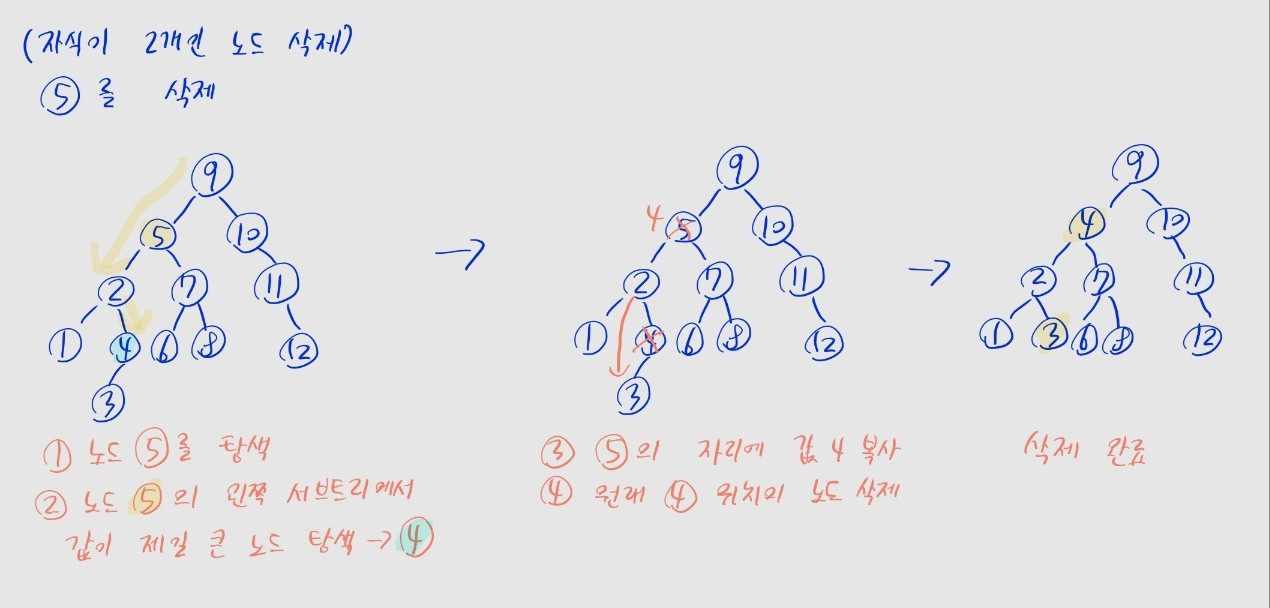
• (1) 삭제할 노드의 왼쪽 서브트리에서 최댓값 노드를 검색
  • 말이 어려운데, 삭제할 노드보다 작은 값 중 최댓값을 찾는 과정임
  • 처음에만 왼쪽자식 으로 이동하고 (왼쪽 서브트리)
  • 다음엔 계속 오른쪽자식으로 이동하면 됨 (더 큰 값)
• (2) 검색한 노드의 값을, 삭제할 노드 위치에 복사
• (3) 검색한 위치의 노드를 삭제
  • 해당 노드가 리프면, 리프 노드일 때와 같이 삭제
  • 해당 노드가 자식이 1개라면, 자식이 1개인 노드일 때와 같이 삭제

🤔 검색한 위치의 노드에 왼쪽, 오른쪽 자식이 모두 있으면 어떡하죠?

• 그럴 일은 절대로 없습니다. 오른쪽 자식에는 현재 노드보다 더 큰 값만 올 수 있다는 점 기억하시죠?
• 오른쪽 자식이 존재한다면, 거기로 더 이동했을 테니 지금 값이 최댓값일 수가 없습니다.

최종 코드

class Node:
    def __init__(self, value):
        self.left = None
        self.right = None
        self.value = value

class SearchTree:
    def __init__(self):
        self.root = None

    # 노드 삽입
    def insert(self, target):
        # 루트노드가 없을 때
        if self.root is None:
            self.root = Node(target)
        else:
            curr = self.root
            while True:
                # 왼쪽자식 추가
                if target < curr.value:
                    if curr.left is None:
                        curr.left = Node(target)
                        break
                    curr = curr.left

                # 오른쪽자식 추가
                if curr.value < target:
                    if curr.right is None:
                        curr.right = Node(target)
                        break
                    curr = curr.right
                
                # 동일 값 존재 시 추가 불가
                if curr.value == target:
                    break

    # 노드 검색
    def search(self, target):
        curr = self.root
        while curr:
            if curr.value == target:
                return True
            elif target < curr.value:
                curr = curr.left
            elif curr.value < target:
                curr = curr.right
        return False

    # class SearchTree 계속
    # 전위 순회: 루트 -> 현재 -> 오른쪽
    def preorder(self, node):
        if node:
            print(node.value, end=' ')
            self.preorder(node.left)
            self.preorder(node.right)

    # 중위 순회: 왼쪽 -> 현재 -> 오른쪽
    def inorder(self, node):
        if node:
            self.inorder(node.left)
            print(node.value, end=' ')
            self.inorder(node.right)

    # 후위 순회: 왼쪽 -> 오른쪽 -> 현재
    def postorder(self, node):
        if node:
            self.postorder(node.left)
            self.postorder(node.right)
            print(node.value, end=' ')

• 실제로 트리를 만든 뒤 전위 / 중위 / 후위 순회를 해 보겠습니다.

tree = SearchTree()
for num in [7, 3, 9, 1, 5, 8, 10]:
    tree.insert(num)

print("전위 순회")
tree.preorder(tree.root) # 7 3 1 5 9 8 10
print("중위 순회")
tree.inorder(tree.root)  # 1 3 5 7 8 9 10
print("후위 순회")
tree.postorder(tree.root) # 1 5 3 8 10 9 7

시간 복잡도

• 트리의 원소가 $N$개일 때

전위, 중위, 후위 순회

• 트리의 모든 값을 탐색하므로, $O(N)$

특정 값 탐색

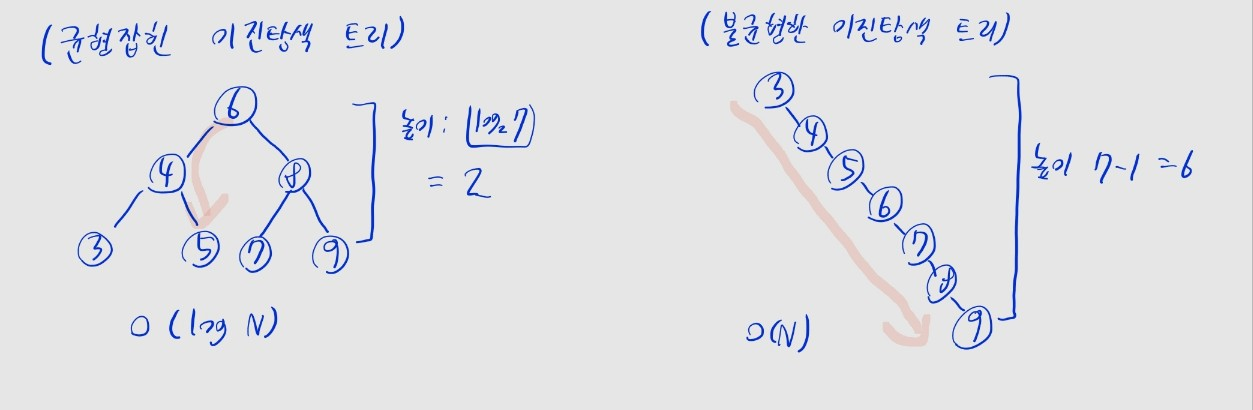
• 트리가 균형잡힌 경우, 평균 $O(\log N)$
  • e.g., 완전 이진 트리처럼 좌우로 균등하게 노드가 분포된 경우, 높이는 약 $\log N$
  • 탐색 시 루트에서 리프까지 최대 $\log N$개의 간선을 거치므로, 시간 복잡도는 $O(\log N)$
• 단 트리가 한쪽으로 치우친 경우, 최악 $O(N)$
  • e.g., 한쪽 방향만 계속 노드가 삽입되어, 선형 리스트와 다를 바 없는 경우
  • 탐색 시 루트에서 리프까지 최대 $N - 1$개의 간선을 거치므로, 시간 복잡도는 $O(N)$

삽입 및 삭제

• 삽입, 삭제 과정에서도 삽입할 위치 / 삭제할 위치까지 이동해야 함
• 결국 평균 $O(\log N)$, 최악 $O(N)$

🤔 트리가 균형잡혀 있는지 불균형한지는 어떻게 결정되나요?

• 원소가 삽입되는 순서에 따라 달라집니다. 사실 위 그림에 있는 두 트리는 양쪽 다 3, 4, 5, 6, 7, 8, 9를 원소로 갖고 있습니다.
• 왼쪽 트리는 순서가 6 -> 4 -> 8 -> 3 -> 5 -> 7 -> 9 순으로 입력되어, 균형되게 유지됐습니다.
• 하지만 오른쪽 트리는 순서가 3 -> 4 -> 5 -> 6 -> 7 -> 8 -> 9 순으로 삽입된 탓에, 오른쪽 자식으로만 노드가 추가돼서 불균형한 트리가 된 거죠.

문제풀이

1991. 트리 순회

백준 / 실버 1 / 트리 순회

• 클래스를 매번 만들기 번거로우면, 파이썬 딕셔너리로 트리를 구현할 수 있음
• 각 노드를 키-값 쌍으로 저장: 키 -> 현재 노드, 값 -> `(왼쪽 자식, 오른쪽 자식)
  • 자식이 없는 경우 None 처리

입력

# 입력이 다음과 같을 때
7		# 이진 트리 노드의 개수

# 순서대로 각 노드, 왼쪽 자식 노드, 오른족 자식 노드의 이름
# '.': 자식노드가 없다는 뜻
A B C
B D .
C E F
E . .
F . G
D . .
G . .

트리 만들기

for _ in range(N):
    node, left, right = input().split()
    tree[node] = (left, right)
 
print(tree)
# {'A': ('B', 'C'), 'B': ('D', '.'), 'C': ('E', 'F'), E': ('.', '.'), 'F': ('.', 'G'), 'D': ('.', '.'), G': ('.', '.')}

전위, 중위, 후위 순회

• 왼쪽 자식에 접근할 때 tree[node][0]을 매개변수로 재귀 호출
• 오른쪽 자식에 접근할 때 tree[node][1]을 매개변수로 재귀 호출
• 값이 .인 경우 없는 노드 -> 종료 조건

# 전위 순회
def preorder(node):
    if node != ".":
        print(node, end="")
        preorder(tree[node][0])
        preorder(tree[node][1])
    
# 중위 순회
def inorder(node):
    if node != ".":
        inorder(tree[node][0])
        print(node, end="")
        inorder(tree[node][1])
    
# 후위 순회
def postorder(node):
    if node != ".":
        postorder(tree[node][0])
        postorder(tree[node][1])
        print(node, end="")

# 루트 노드인 'A'부터 출발
preorder('A')
print()
inorder('A')
print()
postorder('A')

5639. 이진 검색 트리

백준 / 골드 4 / 5639. 이진 검색 트리

• 사실 전위 순회를 한 순서 = 트리에 노드를 삽입한 순서
• 즉, 트리를 구현해 전위 순회 순서대로 삽입하고
• 후위 순회를 재귀로 구현하기
• 재귀 제한 빡빡하다... sys.setrecursionlimit(10 ** 9)로 설정

import sys
input = sys.stdin.readline
sys.setrecursionlimit(10**9)

class Node:
    def __init__(self, x):
        self.value = x
        self.left = None
        self.right = None
        
class Tree:
    def __init__(self):
        self.root = None
    
    def insert(self, x):
        if self.root is None:
            self.root = Node(x)
            
        curr = self.root
        while curr is not None:
            parent = curr
            if x < curr.value:
                is_left = True
                curr = curr.left
            elif x > curr.value:
                is_left = False
                curr = curr.right
            elif x == curr.value:
                return False
        
        if is_left:
            parent.left = Node(x)
        else:
            parent.right = Node(x)
 
tree = Tree()
while True:
    try:
        x = int(input())
        tree.insert(x)
    except:
        break

def postorder(tree, node):
    if node is not None:
        postorder(tree, node.left)
        postorder(tree, node.right)
        print(node.value)
        
postorder(tree, tree.root)