그래프의 대표적인 구현 방식인 인접 행렬, 인접 리스트에 대해 알아봅시다.

그래프

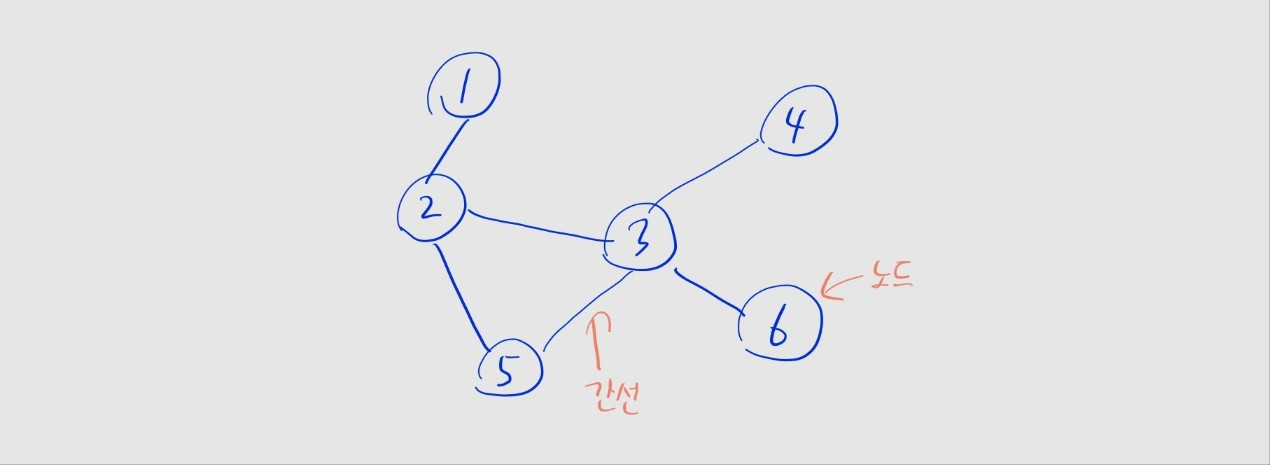
• 그래프는 노드와 간선으로 구성된 자료구조
  • 노드: 데이터 값을 가지는 원소
  • 간선: 노드와 노드를 연결하는 선
• 보통 그래프에서는 특정 노드를 탐색하기 위해, 간선을 따라 노드 간 이동하는 방식의 알고리즘이 사용됨
• 꼭 그래프의 모든 노드가 연결되어 있을 필요는 없음

간선의 방향성

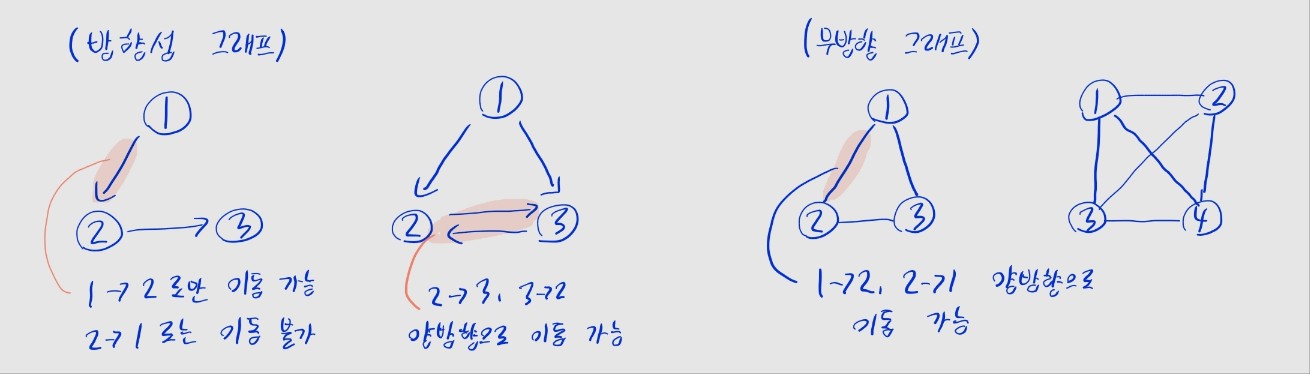
• 방향성 그래프: 간선에 방향이 존재하는 그래프
  • 노드 A -> B 방향의 간선이 있으면, 이 가선을 통해 A -> B로 갈 수 있지만 B -> A론 갈 수 없음
• 무방향 그래프: 모든 간선에서 양방향으로 이동이 가능
  • 노드 A와 B 간 간선이 있으면, A -> B, B -> A 어느 방향이든 이동 가능

⚠️ 방향성 그래프에서도 A -> B 방향과 B -> A 방향의 간선이 모두 존재하면, 양방향 이동이 가능합니다. 위 그림의 2번째 방향성 그래프를 참고하세요.

간선의 가중치

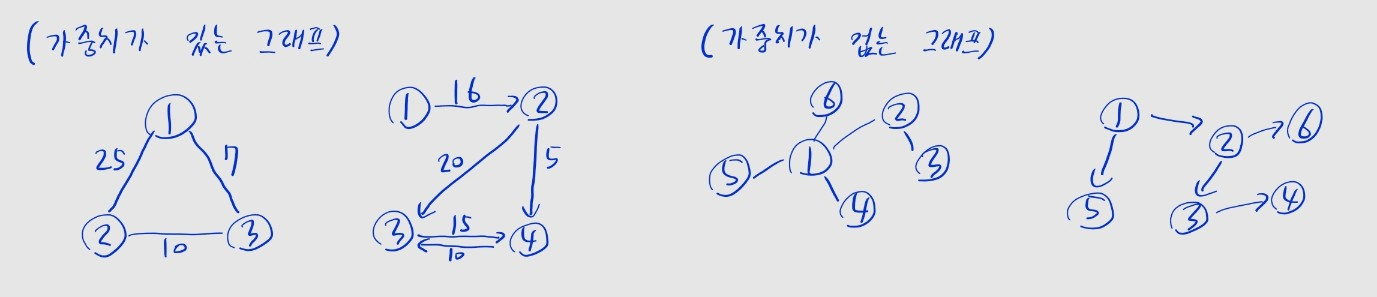
• 그래프에는 두 노드 사이 간선에 가중치가 존재할 수 있음
• 일반적으로 가중치는 해당 간선을 통해 이동했을 때 비용으로 해석되어, 이를 최소화하는 것을 목표로 함
  • 최소 비용 알고리즘은 그래프의 모든 노드를 탐색했을 때, 지나간 간선들의 가중치 합이 최소가 되도록 하는 경로를 탐색함

• 가중치가 명시되지 않은 그래프 -> 모든 간선의 가중치를 동일하게 1로 간주

사이클

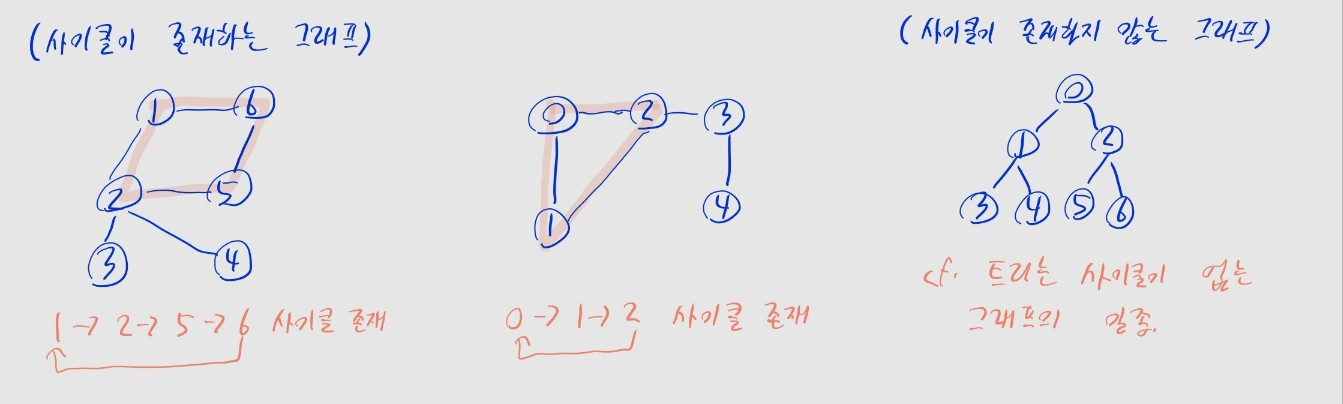
• 그래프 내 출발한 노드로 돌아오는 경로
  • e.g., 정점 A -> B -> C -> A
• 즉, 그래프의 특정 노드에서 출발해서 여러 간선을 따라 이동한 후, 다시 같은 노드로 돌아올 수 있으면 사이클이 존재
  • 단, 도중에 동일한 노드나 간선을 두 번 이상 지나선 안 됨

🤔 트리도 노드와 간선을 연결했던 것 같은데요, 트리랑 그래프는 뭔 차이가 있나요?

• 트리도 그래프의 한 종류라고 볼 수 있습니다. 노드 간에 부모 - 자식 관계가 존재하는 그래프가 트리인 거죠.
• 정확히는 트리는 사이클이 없고, 모든 노드가 연결된 무방향 그래프입니다. (외울 필요는 절대 없습니다...)

행렬의 표현 방식

• 노드의 수를 $N$, 간선의 수를 $E$로 둘 때
• 두 가지 방법이 있는데, 보통은 백준 문제 입력 형식에 따라 더 나은 방식을 찾아서 선택합니다

인접 행렬

• $N \times N$ 크기의 2차원 행렬로 간선 정보를 저장
• 행렬의 $i$행 $j$열엔, $i$번째 노드 -> $j$번째 노드로 가는 간선의 가중치를 저장
  • 무방향 그래프이면 양쪽 방향 다 저장해야 함
• 두 노드를 잇는 간선이 없을 시, 무한대 값 저장 (float('inf'))
• 가중치가 명시되지 않은 그래프일 시, 간선이 있으면 1, 없으면 무한대 값 저장

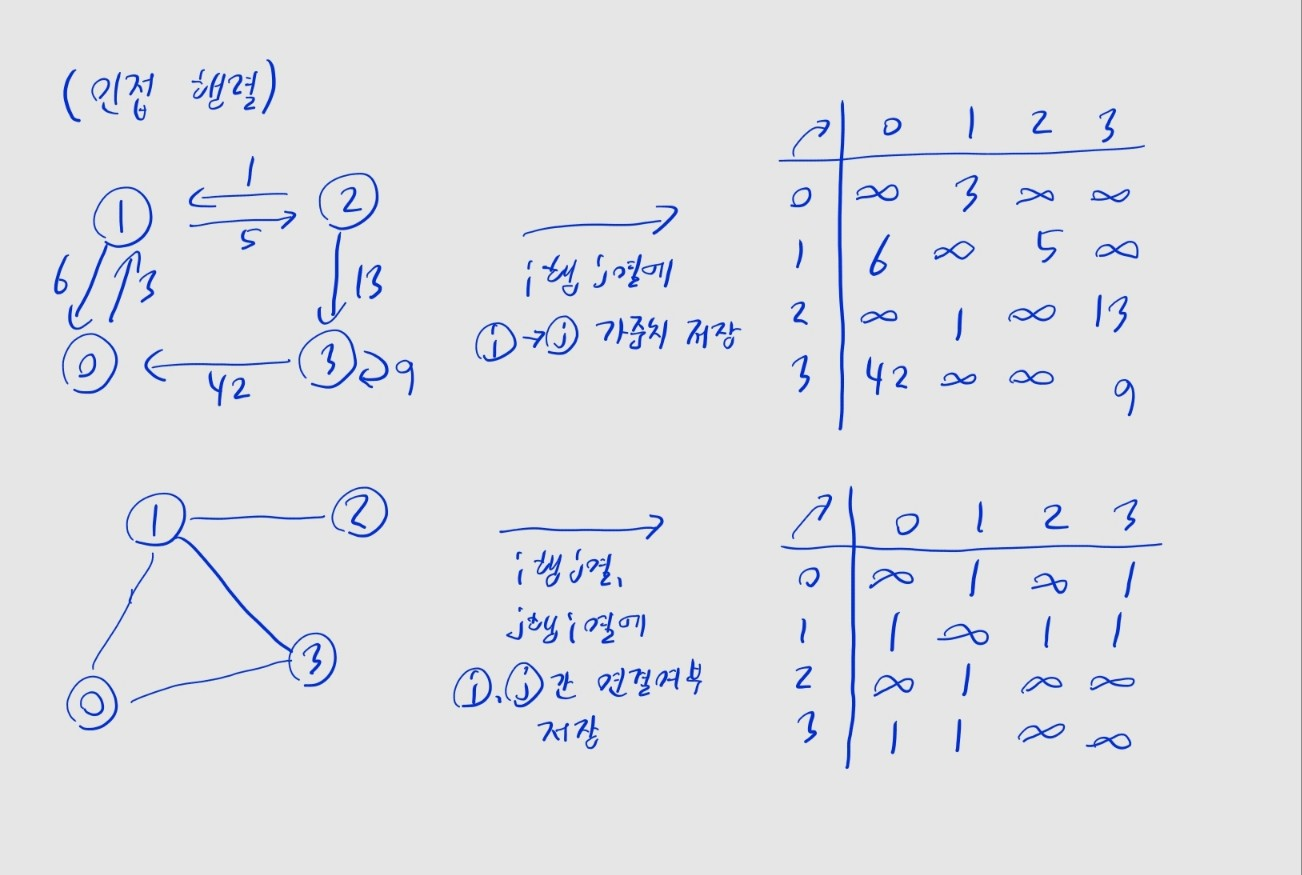
🤔 첫 그래프에 노드 자기 자신이랑 연결된 간선이 있는데 제가 잘못 본 건가요?

• 실제로 그런 간선도 그래프에 있을 수 있습니다. 이걸 자기 루프(self loop)라고 하며, 이 간선 하나만 타면 바로 자기 자신으로 돌아오니 그래프엔 사이클이 존재합니다.

INF = float('inf')

# 사진 왼쪽의 그래프
graphA = [[INF, 3, INF, INF],
         [6, INF, 5, INF],
         [INF, 1, INF, 13],
         [42, INF, INF, 9]]

# 사진 오른쪽의 그래프
graphB = [[INF, 1, INF, 1],
          [1, INF, 1, 1],
          [INF, 1, INF, INF],
          [1, 1, INF, INF]]

시간 복잡도

• 노드의 수를 $N$으로 둘 때
• 두 노드 간 간선의 가중치 / 존재 여부를 확인할 때: $O(1)$
  • graphA[i][j] 인덱싱 연산으로 끝
• 특정 출발 노드의 모든 간선을 확인할 때: $O(N)$
  • graphA[i]의 모든 원소를 탐색해야 함

공간 복잡도

• 행, 열의 수가 $N$개인 행렬을 만들어야 함: $O(N^2)$
• 노드 수에 비해 간선 수가 매우 적은 희소 행렬인 경우, 비효율적
  • 거의 모든 원소가 무한대 값이 되기 때문

인접 리스트

• 시작 노드를 전체 노드 개수 크기의 1차원 배열로 표현
• 배열의 인덱스를 시작 노드로 생각하여, 간선으로 연결된 노드들을 연결 리스트의 형태로 관리
  • 노드 객체에는 (노드 번호, 간선 가중치)를 저장
  • 가중치가 명시되지 않은 그래프일 시, 노드 번호만 저장해도 됨

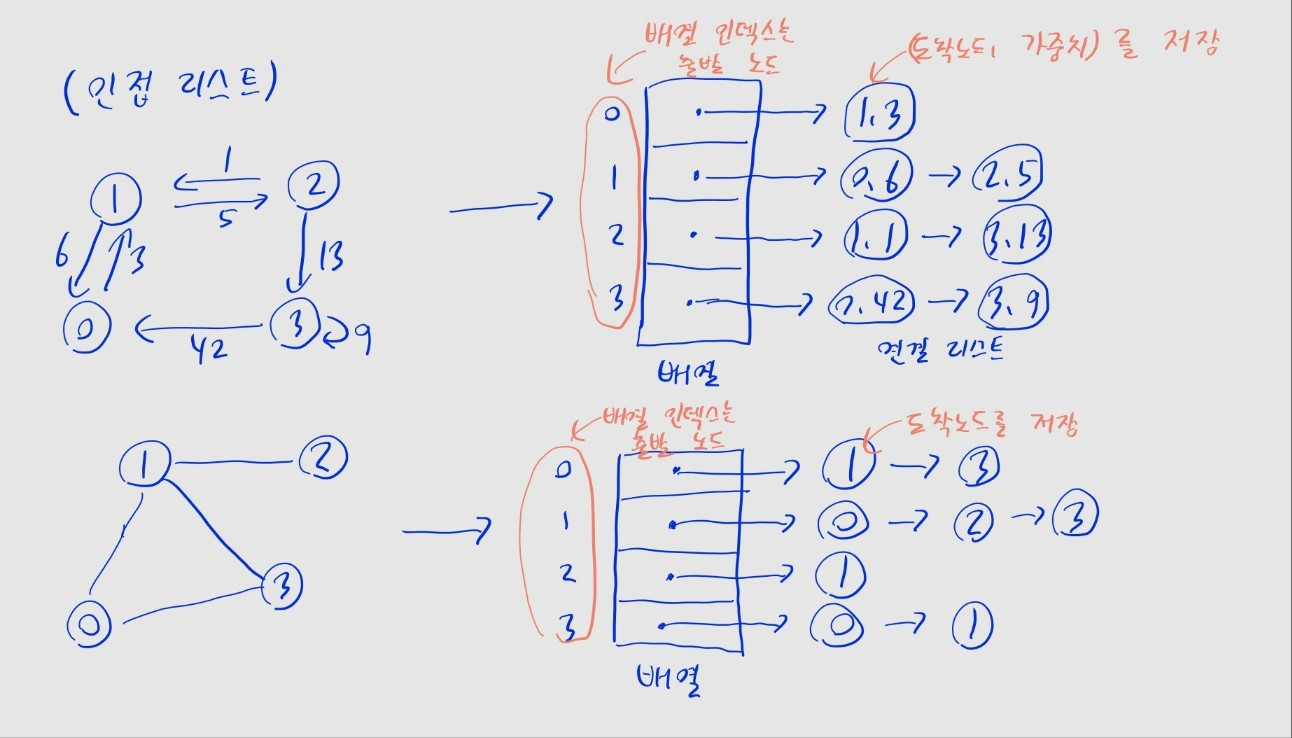
• 하지만 파이썬으로는 굳이 불편한 연결 리스트를 쓸 필요는 없음
• 2차원 리스트로 관리 가능: 각 인덱스는 시작 노드, 그 인덱스에 해당하는 리스트가 인접 노드 목록이 되는 형태
  • 시작 노드 값을 key, 인접 노드로 구성된 리스트를 value로 설정한 딕셔너리로도 구현 가능

# 2차원리스트 사용
# 사진 왼쪽의 그래프
graphA = [
	[(1, 3)],
    [(0, 6), (2, 5)],
    [(1, 1), (3, 13)],
    [(0, 42), (3, 9)]
]

# 사진 오른쪽의 그래프
graphB = [
	[1, 3],
    [0, 2, 3],
    [1],
    [0, 1]
]

# 딕셔너리 사용
# 사진 왼쪽의 그래프
graphA = {
    0: [(1, 3)],
    1: [(0, 6), (2, 5)],
    2: [(1, 1), (3, 13)],
    3: [(0, 42), (3, 9)]
}

# 사진 오른쪽의 그래프
graphB = {
    0: [1, 3],
    1: [0, 2, 3],
    2: [1],
    3: [0, 1]
}

시간 복잡도

• 노드의 수를 $N$으로 둘 때
• 두 노드 간 간선의 가중치 / 존재 여부를 확인할 때
  • 시작 노드에 연결된 노드 수를 $k$로 둘 때, 평균 $O(k)$, 최악 $O(N)$
  • 연결된 노드 수만큼 연결 리스트의 각 원소를 탐색해야 함
  • 최악의 경우 모든 노드가 연결되어 있을 수 있으니, $O(N)$
• 특정 출발 노드의 모든 간선을 확인할 때
  • 평균 $O(k)$, 최악 $O(N)$
  • 위 연산과 마찬가지

공간 복잡도

• 간선의 수를 $E$로 둘 때
• 시작 노드 정보를 담은, 길이 $N$의 배열을 만들 때 $O(N)$
• 모든 간선 정보를 한 번씩 저장해야 하므로, 간선 수만큼 공간이 필요하니 $O(E)$
• 최종 $O(N + E)$
• 간선 수($E$)가 노드 수($N$)에 비해 적은 경우
  • $O(N^2)$의 공간 복잡도를 가진 인접행렬에 비해 효율적

그래서 뭘 써야 해요?

🚨 인접 행렬

• 노드의 수가 적고, 간선의 수가 많을 때
• 두 노드 간 가중치 정보를 빠르게 확인해야 할 때 ($O(1)$)

🚨 인접 리스트

• 간선의 수가 노드의 수에 비해 많이 적을 때
• 한 노드에서 출발하는 모든 간선을 확인해야 할 때
  • 평균 $O(k)$, 최악 $O(N)$이지만, 보통 한 노드가 모든 노드와 연결되어 있는 일은 적음
  • 따라서 항상 $O(N)$인 인접 행렬에 비해선 일반적으로 빠름