'꼬리에 꼬리를 무는 그날 이야기'라는 프로그램이 있죠. 우리는 '꼬리에 꼬리를 무는 연결 리스트'에 대해 알아보도록 합시다.

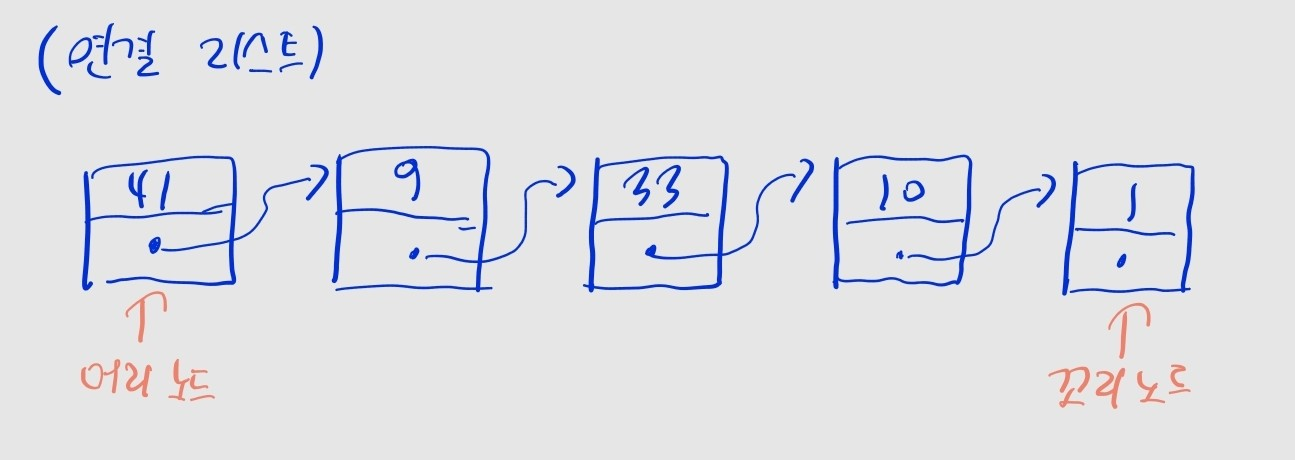
연결 리스트

• 데이터가 순서대로 나열되고, 각 데이터가 화살표로 연결된 구조
• 노드: 연결 리스트의 각 원소
  • 노드는 데이터와 뒤쪽 노드를 가리키는 포인터를 가짐
• 머리 노드: 맨 앞의 노드
• 꼬리 노드: 맨 뒤의 노드

포인터를 이용한 연결 리스트

• 실제 코딩 테스트에서 이렇게 연결 리스트를 구현할 일은 없습니다.
• 하지만 연결 리스트에서의 삽입, 삭제, 탐색을 이해하려면 직접 구현해 보면 좋습니다.

노드 클래스 만들기

• data 속성: 노드가 저장하는 데이터 값
• next 속성: 다음 노드를 가리키며, 다른 Node 인스턴스를 참조
• 이렇게 동일한 형의 인스턴스를 참조하는 속성이 있는 구조를 자기 참조형이라 함

class Node:
    def __init__(self, data=None, next=None):
        self.data = data # 저장값
        self.next = next # 다음 노드

연결 리스트 클래스 만들기

class LinkedList:
    def __init__(self):
        # 노드가 없는 빈 연결 리스트 생성
        self.head = None    # 머리 노드

    # 이후 메서드는 뒤에서 구현

속성 정의

• head 속성: 머리 노드를 참조
• head가 None인 경우: 노드가 하나도 없는, 빈 연결 리스트

머리에 노드 삽입

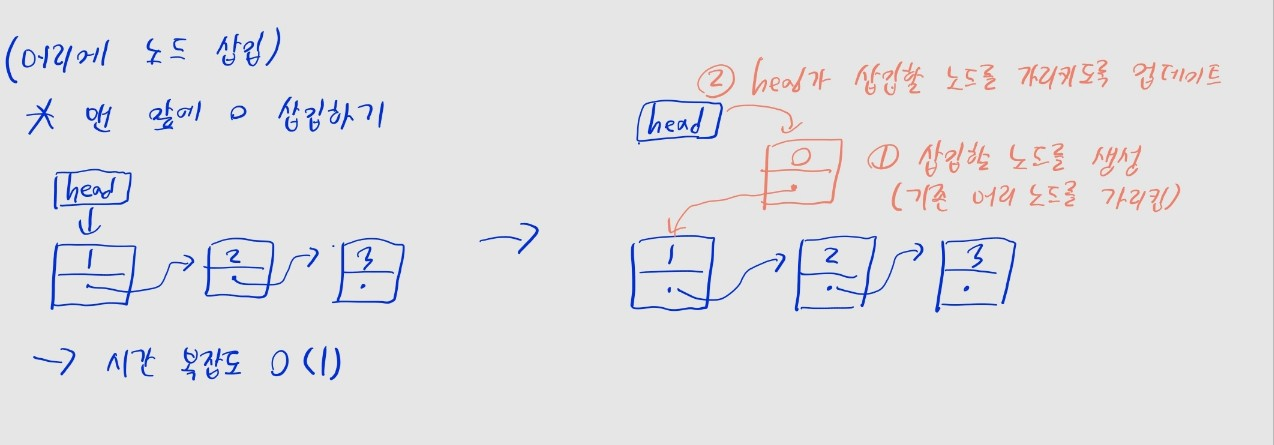
• (1단계) 삽입할 노드를 생성한다.
  • 기존의 머리 노드를 가리키게 한다.
• (2단계) head가 새로 삽입한 노드를 가리키도록 수정한다.

# 머리에 노드 삽입
def add_first(self, x):
    # (1) 삽입할 노드를 생성한다.
    insert_node = Node(data=x, next=self.head)
    # (2) `head`가 새로 삽입한 노드를 가리키도록 수정한다.
    self.head = insert_node

• 시간 복잡도 $O(1)$ - 원소 수와 무관하게 위 두 연산만 진행

임의 위치에 노드 삽입

• (1단계) 삽입할 위치 이전에 위치한 노드 prev를 찾는다.
• (2단계) 삽입할 노드를 생성한다.
  • 다음 노드로, prev의 다음 노드를 설정한다.
• (3단계) prev의 다음 노드를, 새로 생성한 노드로 변경한다.
• 단 맨 앞에 노드를 삽입하는 경우, 이전 노드가 존재하지 않으므로 위 과정 수행 불가능
  • <머리에 노드 삽입>대로 진행한다.

# where번째 위치에 노드 삽입
def add(self, x, where):
  # 맨 앞에 삽입하는 경우
  if where == 0:
      self.add_first(x)
      return

  # (1) 삽입 위치 이전에 위치한 노드 `prev` 찾기
  prev = self.head
  i = 0

  while prev is not None and i < where - 1:
      prev = prev.next
      i += 1

  if prev is None:
      print("삽입 위치가 인덱스 길이보다 큽니다")
      return

  # (2) 삽입할 노드를 생성
  insert_node = Node(data=x, next=prev.next)

  # (3) prev의 다음 노드를 새로 생성한 노드로 변경
  prev.next = insert_node

• 시간 복잡도 $O(N)$ - 삽입 위치의 앞쪽 노드까지 이동해야 함

임의 위치의 노드 확인

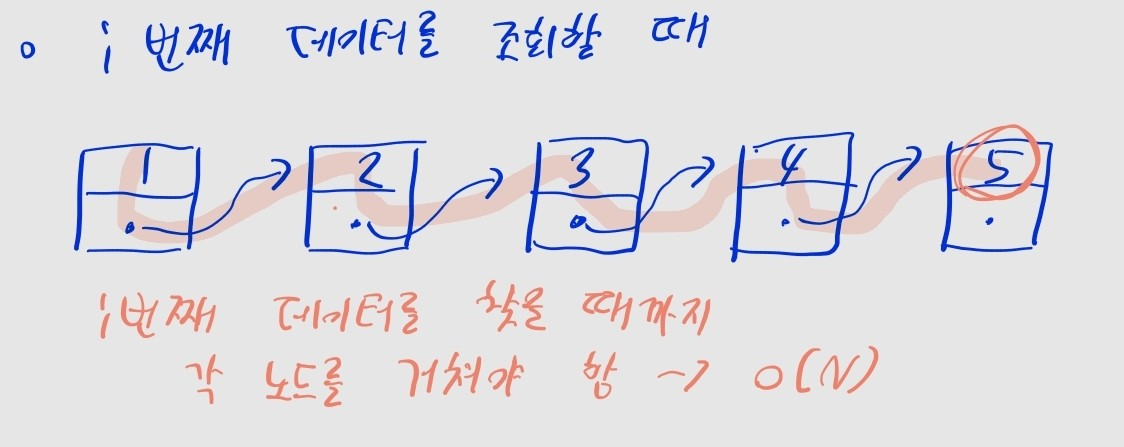
• 머리 노드부터 찾고자 하는 위치의 노드까지 이동한다.

# where번째 위치의 노드 데이터 확인
def index(self, where):
  curr = self.head
  i = 0
  # 찾고자 하는 위치의 노드까지 이동
  while curr is not None and i < where:
      curr = curr.next
      i += 1
  if curr is None:
      print("탐색 위치가 인덱스 길이보다 큽니다")
      return
  return curr.data

• 시간 복잡도 $O(N)$ - 삽입 위치까지 이동해야 함

머리 노드 삭제

• head가 기존 머리 노드의 다음 노드 head.next를 가리키도록 업데이트한다.
• 이후 기존 머리 노드는 어디에서도 접근할 수 없게 된다.

# 머리 노드 삭제
def remove_first(self):
    # 연결 리스트가 비어 있지 않아야 함
    if self.head is not None:
        # 기존 머리 노드의 다음 노드로 업데이트
        self.head = self.head.next

• 시간 복잡도 $O(1)$ - 원소 수와 무관하게 위 두 연산만 진행

임의 위치의 노드 삭제

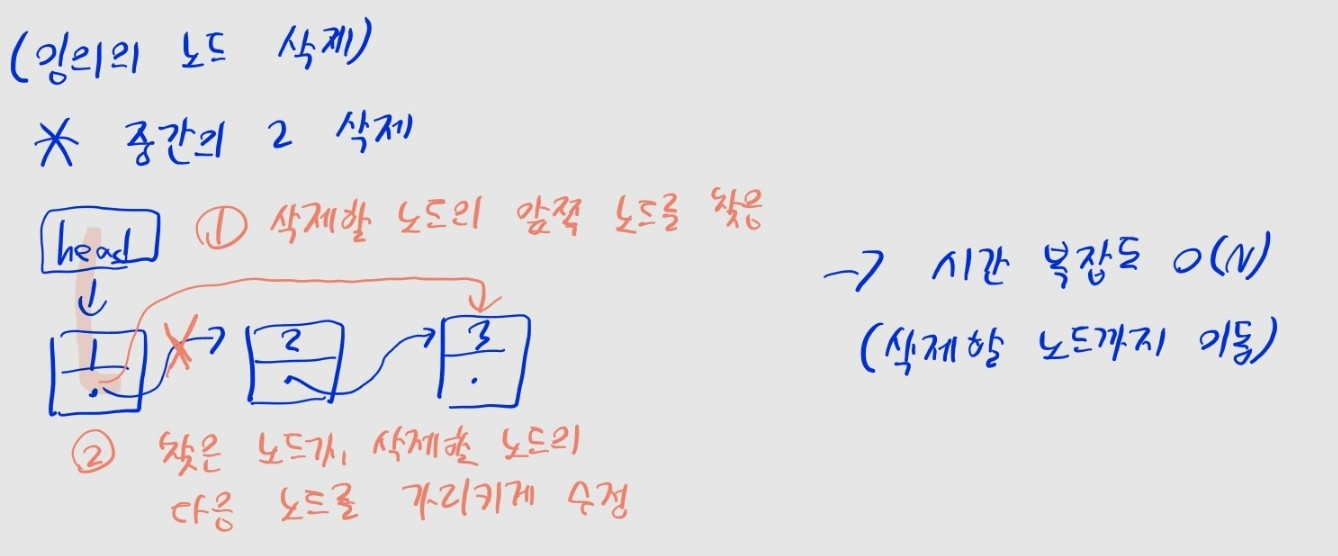
• (1단계) 삭제할 노드 앞에 위치한 노드 prev를 찾는다.
• (2단계) prev의 다음 노드를, 삭제할 노드의 다음 노드로 업데이트한다.
• 이후 삭제된 노드는 어디에서도 접근할 수 없게 된다.
• 단 맨 앞 노드를 삭제하는 경우, 이전 노드가 존재하지 않으므로 위 과정 수행 불가능
  • <머리 노드 삭제>대로 진행한다.

# where번째 위치의 노드 삭제
def remove(self, where):
    # 연결 리스트가 비어 있지 않아야 함
    if self.head is not None:
        # 첫 노드를 삭제하는 경우
        if where == 0:
            self.remove_first()
            return

        # (1) 삭제할 노드 앞에 위치한 노드 `prev`를 찾는다.
        prev = self.head
        i = 0

        while prev is not None and i < where - 1:
            prev = prev.next
            i += 1

        if prev is None or prev.next is None:
            print("삭제 위치가 인덱스 길이보다 큽니다")
            return

        # (2) `prev`의 다음 노드를, 삭제할 노드의 다음 노드로 업데이트
        prev.next = prev.next.next

• 시간 복잡도 $O(N)$ - 삭제 위치의 앞쪽 노드까지 이동해야 함

배열 vs 연결 리스트

• 맨 앞에 값 삽입

  • 배열 $O(N)$: 삽입/삭제된 위치 이후의 원소가 한 칸씩 밀림
  • 연결 리스트 $O(1)$: head가 가리키는 노드만 바꿔 주면 됨

• 중간에 값 삽입 / 삭제

  • 배열 $O(N)$: 삽입/삭제된 위치 이후의 원소가 한 칸씩 밀림
  • 연결 리스트 $O(N)$: 삽입/삭제할 위치의 앞쪽 노드까지 이동해야 함

• 맨 끝에 값 삽입 / 삭제

  • 배열 $O(1)$: 원소의 이동이 발생하지 않음
  • 연결 리스트 $O(N)$: 꼬리 노드까지 이동해야 함

• i번째 원소 접근

  • 배열 $O(1)$: A[i]로 바로 가능
  • 연결 리스트 $O(N)$: 0번째 ~ i-1번째 노드를 거쳐야 함

원형 이중 연결 리스트

• 🤔 그러면 연결 리스트는 맨 앞에 원소를 삽입하거나, 맨 앞 원소를 삭제할 때만 빠른 성능이 보장되나요?
  • 그렇습니다. 대신 연결 리스트를 응용해서, 맨 앞 / 맨 뒤 양쪽에서의 삽입 / 삭제할 때 모두 $O(1)$이 걸리게끔 만들 수 있습니다. 배열과 연결 리스트의 장점을 모두 살린 셈이죠. 이게 바로 지금 배울 원형 이중 연결 리스트입니다.

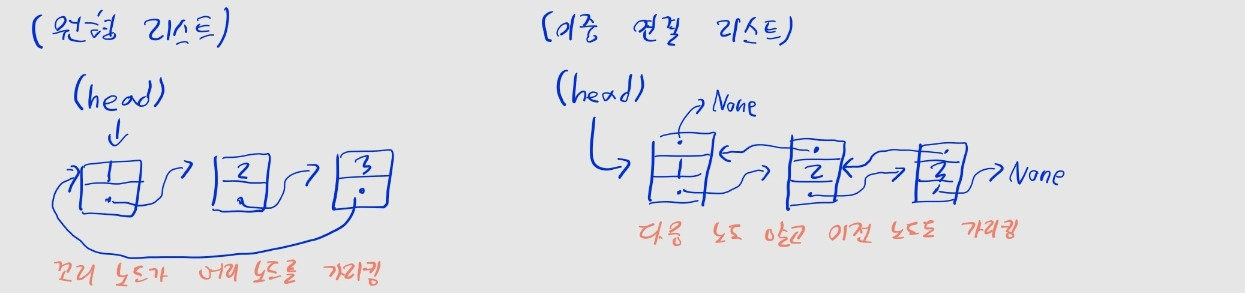
• 원형 리스트
  • 꼬리 노드가 다시 머리 노드를 가리킴
• 이중 연결 리스트
  • 앞쪽 노드를 찾을 수 있는 포인터가 주어짐

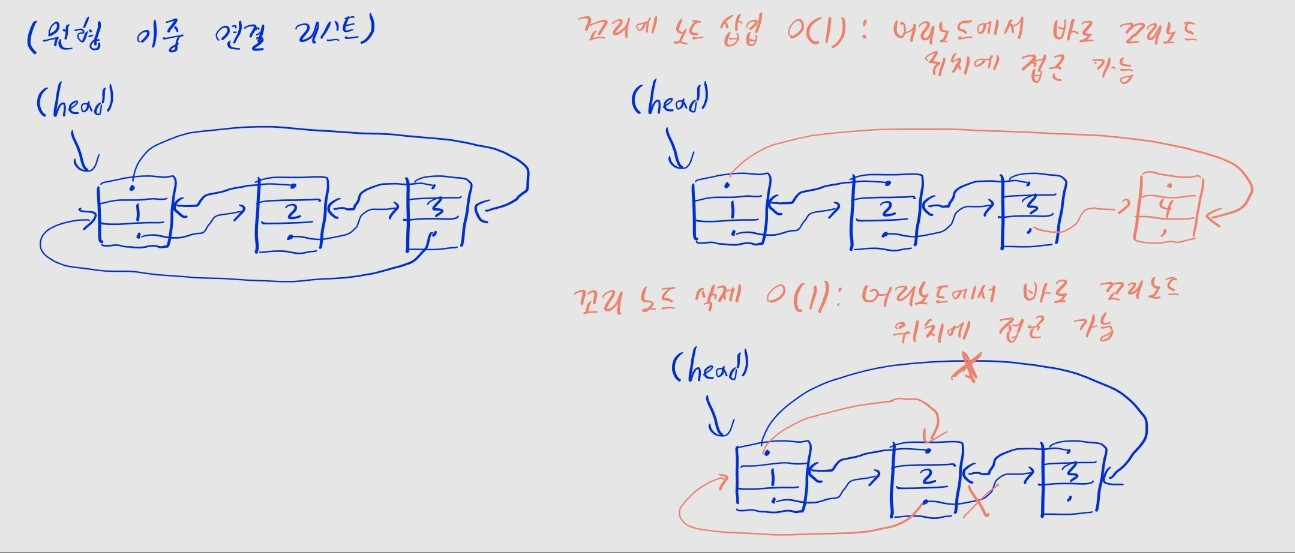
• 원형 이중 연결 리스트
  • 원형 리스트 + 이중 연결 리스트
  • 머리 노드의 앞쪽 포인터가 꼬리 노드를 가리킴

• 장점: 꼬리 위치에 노드를 삽입하거나, 꼬리 노드를 삭제할 때, $O(N)$이 아닌 $O(1)$ 소요
  • 머리 노드에서 꼬리 노드 위치로 바로 접근할 수 있기 때문
• 머리 위치에 노드를 삽입하거나, 머리 노드를 삭제하는 연산은 여전히 $O(1)$

deque

🤔 그래서 이중 연결 리스트가 뭔지는 알겠는데, 실제로 파이썬에서 이걸 활용하는 자료구조가 있나요?

• 파이썬의 collections.deque 자료구조는 이중 원형 연결 리스트와 유사하게 구현되어 있습니다.
  • 엄밀히 말해선 원형은 아니고, 원형처럼 작동하게끔 설계되었다고 합니다. 이건 설명 생략
• list의 경우, 맨 앞에 원소를 추가 (list.insert(0, x))하거나 제거 (list.pop(0))할 때 $O(N)$이 소요됐었죠.
• 하지만 deque는 연결 리스트로 구현되어 있으니, 맨 앞 원소를 list보다 빠른 $O(1)$에 제거/삽입할 수 있습니다.
  • deque.appendleft(): 맨 앞에 원소를 삽입, $O(1)$
  • deque.popleft(): 맨 앞 원소를 꺼내 반환, $O(1)$
• 맨 뒤 원소 역시 list와 동일하게 $O(1)$에 제거/삽입할 수 있습니다.
  • deque.append(), deque.pop()은 여전히 사용 가능하고, $O(1)$ 소요
• deque에서도 인덱스를 이용해 특정 위치의 원소에 접근할 수 있습니다.
  • 하지만 연결 리스트처럼 노드에서 노드로 이동하는 방식이라 $O(N)$이 소요됩니다.
  • 즉 인덱싱, 슬라이싱이 필요하면 list로 변환한 후 하는 게 좋습니다.

from collections import deque

a = deque([1, 2, 3])
a.appendleft(0)
print(a)  	# deque([0, 1, 2, 3]), O(1)
a.popleft()
print(a)  	# deque([1, 2, 3]), O(1)
print(a[1]) # 2, O(N)

정리

연산	배열 OR list	연결 리스트	이중 원형 연결 리스트 OR deque
맨 앞 원소 삽입/삭제	$O(N)$	$O(1)$	$O(1)$
중간에 원소 삽입	$O(N)$	$O(N)$	$O(N)$
맨 뒤 원소 삽입/삭제	$O(1)$	$O(N)$	$O(1)$
원하는 위치의 원소 탐색	$O(1)$	$O(N)$	$O(N)$