술자리에서 숫자 맞추기 업다운 게임을 할땐 보통 가운데 숫자부터 불러보죠. 그게 바로 이분 탐색입니다.

이분 탐색

• 배열에서 원하는 값의 인덱스를 찾을 수 있는 알고리즘
• 기존의 선형 탐색: 최대 $N$개의 값을 탐색하므로, $O(N)$ 소요
  • 파이썬의 list.index(x) 메서드도 동일 방식이므로 $O(N)$ 소요

A = [1, 2, 3, 4, 5]

for i in range(A):
    if A[i] == 5:
        print(i)    # 4

• 이분 탐색은 $O(\log N)$만에 값을 탐색할 수 있음
• 다만, 이미 원소가 오름차순 혹은 내림차순으로 정렬되어 있어야 함

방법

• 매번 배열 중앙의 원소와 찾는 값을 비교
• 중앙의 원소값 < 찾는 값인 경우, 중앙 인덱스 이전엔 찾는 값이 없음
  • 즉 탐색 범위를 중앙 인덱스 이후로 좁힘
• 중앙의 원소값 > 찾는 값인 경우, 중앙 인덱스 이후엔 찾는 값이 없음
  • 즉 탐색 범위를 중앙 인덱스 이전으로 좁힘
• 값을 찾거나, 더 탐색할 범위가 없을 때까지 반복

함수로 구현하기

• 원소가 총 n개인 배열 A에서, 값 target을 찾을 때
• 검색 범위의 맨 앞, 맨 끝 인덱스를 l, r로 둠
  • 처음엔 전 범위를 검색해야 하므로 l = 0, r = n - 1로 초기화
• 가운데 인덱스 (l + r) // 2를 m으로 둠
• target과 A[m]을 비교
  • A[m] < target인 경우, l을 m + 1로 이동해 검색 범위를 뒤쪽 절반으로 좁힘
  • A[m] > target인 경우, r을 m - 1로 이동해 검색 범위를 앞쪽 절반으로 좁힘
• 종료 조건
  • A[m] == key인 경우, 인덱스 m을 찾았으니 종료
  • 검색 범위가 더 없는 경우 (l > r), 배열에 target이 없으니 종료

# a에서 target 찾기

def binary_search(a, target):
    l = 0                       # 검색 범위 맨 앞의 인덱스
    r = len(a) - 1              # 검색 범위 맨 끝의 인덱스

    while True:
        m = (l + r) // 2        # 중앙 원소의 인덱스

        if a[m] == target:      # target을 찾은 경우
            return m
        elif a[m] < target:     # 인덱스 m 이후에 target 존재
            l = m + 1
        else:
            r = m - 1

        if l > r:               # 더 이상 검색할 값이 없음
            return -1           # 찾지 못한 경우 -1 반환

        print()

a = [5, 7, 15, 28, 29, 31, 39, 53, 68, 70, 95]
binary_search(a, 39) # 6

시간 복잡도

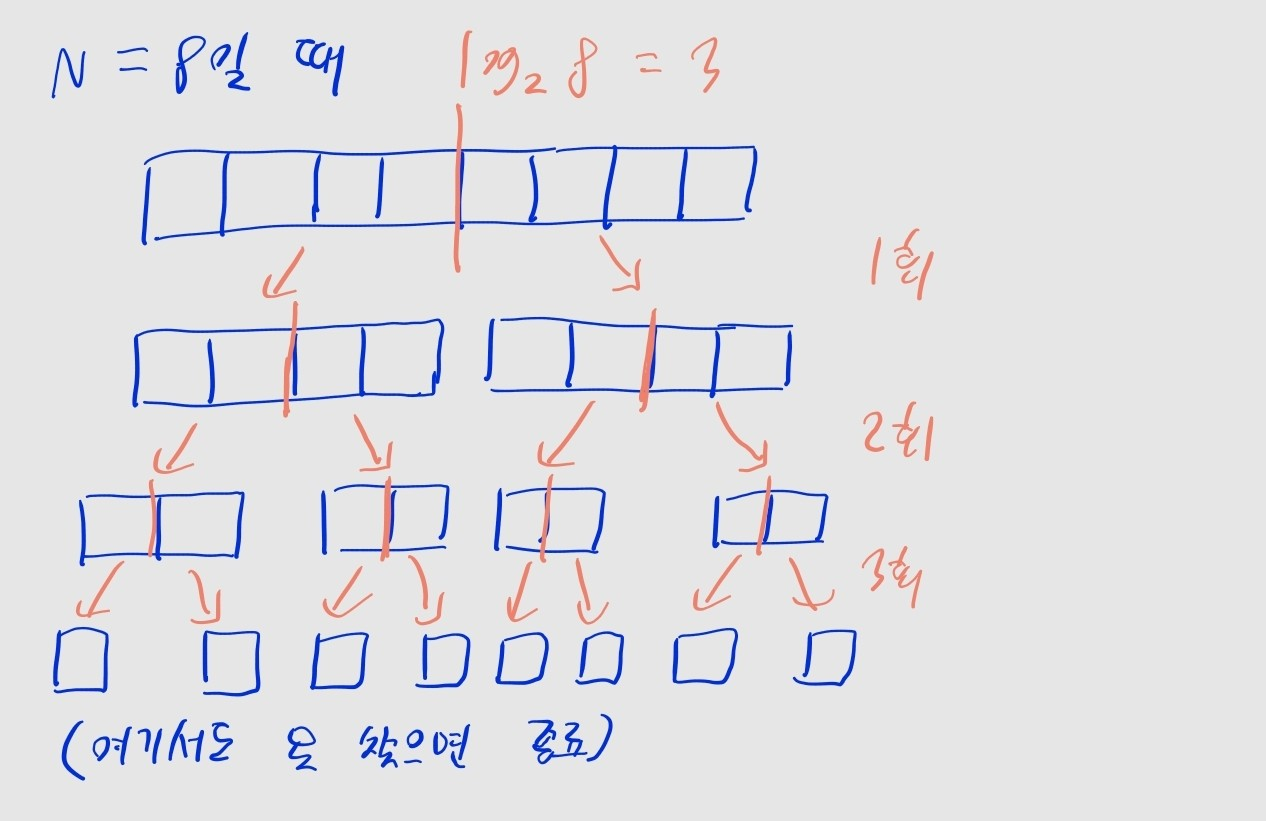
• while문이 1번 반복될 때마다 검색 범위가 절반으로 줄어듦
  • 원소가 $N$개일 때, 약 $\log_{2}N$번 범위를 반으로 나누는 작업을 수행
  • 따라서 시간 복잡도는 $O(\log N)$
• 단, 파이썬 기준 $O(N \log N)$이 소요되는 정렬을 먼저 시도해야 함

bisect 라이브러리

• 파이썬 bisect 라이브러리를 이용해, 직접 함수를 구현하지 않고도 이진 검색을 수행할 수 있음

• 단, 정렬은 먼저 해 와야 함

• bisect.bisect_left(a, x)

  • 리스트 a 내 가장 왼쪽 x의 위치를 반환
  • x가 없는 경우, x를 삽입할 수 있는 위치 반환

import bisect

a = [1, 4, 7, 7, 10, 13]
print(bisect.bisect_left(a, 7)) # 2 (왼쪽 7의 위치)
print(bisect.bisect_left(a, 11)) # 5 (10과 13 사이)

• bisect.bisect_right(a, x)
  • 리스트 a 내 가장 오른쪽 x의 위치 + 1을 반환
  • x가 없는 경우, x를 삽입할 수 있는 위치 반환

import bisect

a = [1, 4, 7, 7, 10, 13]
print(bisect.bisect_right(a, 7)) # 4 (오른쪽 7의 위치 + 1)
print(bisect.bisect_right(a, 11)) # 5 (10과 13 사이)

• 리스트 a 내 x의 원소 개수 구하기
  • bisect_right(a, x) - bisect_left(a, x) 사용 가능
  • 가장 오른쪽 x의 위치 + 1 - 가장 왼쪽 x의 위치이므로, x의 원소 개수를 계산 가능

import bisect

a = [1, 4, 7, 7, 10, 13]
print(bisect.bisect_right(a, 7) - bisect.bisect_left(a, 7))
# 4 - 2 = 2개

문제풀이

2805. 나무 자르기

• 이분탐색은 꼭 배열에서 특정 값을 찾는 데에만 쓰는 건 아니다. 정수 범위 내 특정 조건을 만족하는 수를 찾는 데도 쓸 수 있다.
  풀이가 길어져 별도 글로 대체

2110. 공유기 설치

• 가끔씩은 이분 탐색으로 풀어야 한다는 사실을 떠올리는 거 자체가 고역일 때도 있다.
  풀이가 길어져 별도 글로 대체