내일 시험인데 친구가 술을 먹자고 하네요?

네… 교수님, 죄송합니다. 전 술을 마시러 갑니다.

우선순위 큐 역시 우선순위가 높은 데이터부터 꺼내는 자료구조입니다.

우선순위 큐

• 데이터를 우선순위에 따라 처리하고 싶을 때 사용하는 자료구조
• 인큐할 땐 데이터에 우선순위를 부여해 추가하고, 디큐할 땐 우선순위가 가장 높은 데이터를 꺼냄
• 보통 우선순위는 값의 크기로 결정됨
  • 인큐된 데이터 중 가장 작은 OR 가장 큰 값을 디큐할 수 있음

힙을 이용한 구현

힙의 특징

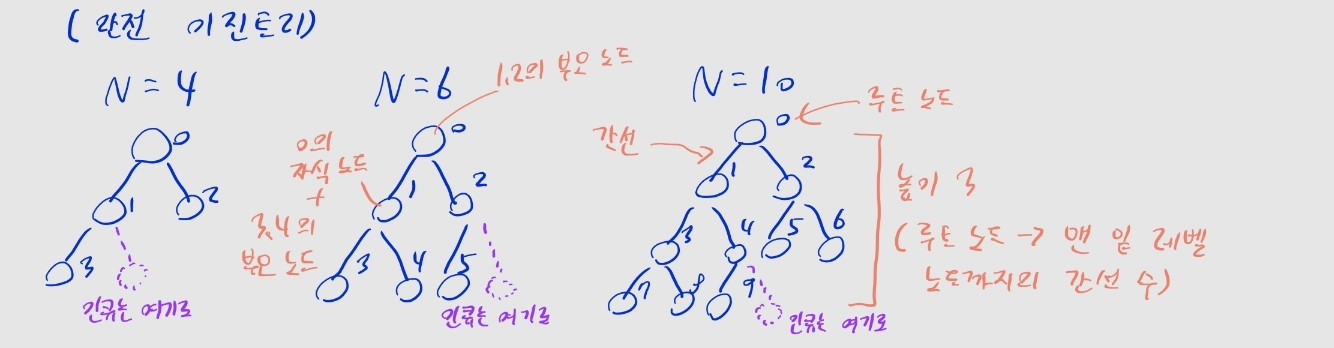
• 힙은 완전 이진 트리의 일종
  • 루트 노드부터 시작해서, 왼쪽 -> 오른쪽 자식 순서대로 데이터가 삽입되는 트리
  • 원소 개수가 $N$개일 때, 완전 이진 트리의 구조는 항상 일정한 형태를 띔

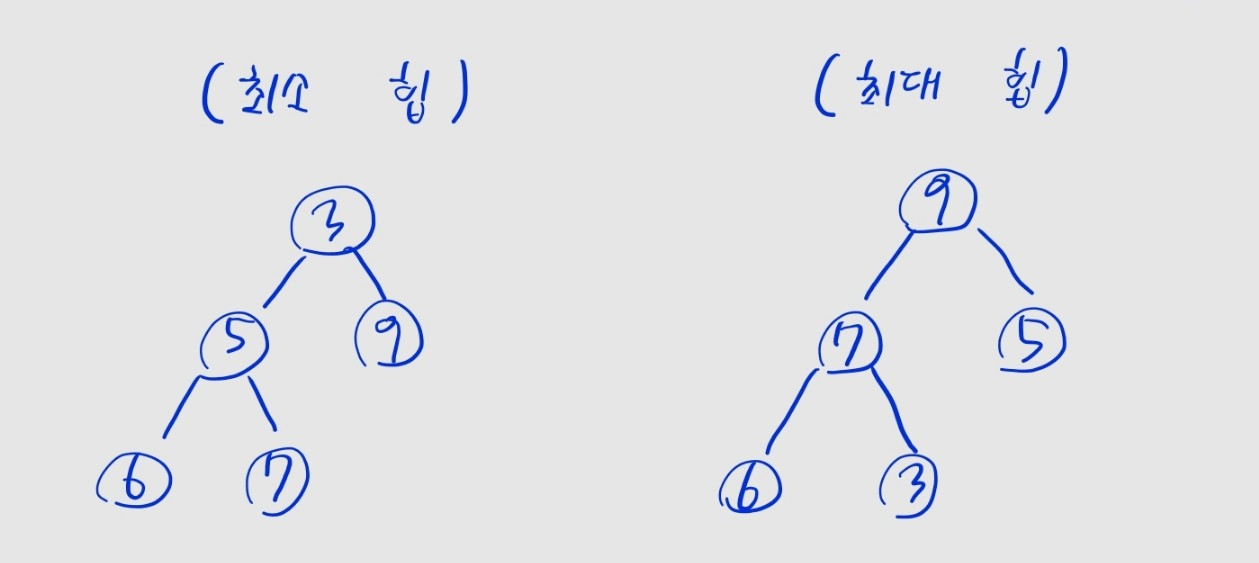
• 최소 힙
  • 부모가 자식 노드보다 작거나 같은 값을 가짐
  • 즉, 루트 노드가 최솟값을 가짐
• 최대 힙
  • 부모가 자식 노드보다 크거나 같은 값을 가짐
  • 즉, 루트 노드가 최댓값을 가짐
• 본 글에선 최소 힙을 기준으로 설명함

• 우선순위 큐에서 디큐할 땐, 힙의 최댓값 또는 최솟값인 루트 노드를 삭제하고 반환
  • 즉, 루트 노드에는 항상 최솟값 또는 최댓값이 위치해야 함 (이걸 '힙 조건을 만족한다'라고 함)
  • 따라서 인큐, 디큐를 수행할 때마다, 힙 조건을 만족하게끔 노드의 위치를 조정할 필요가 있음

인큐 (힙으로 푸시)

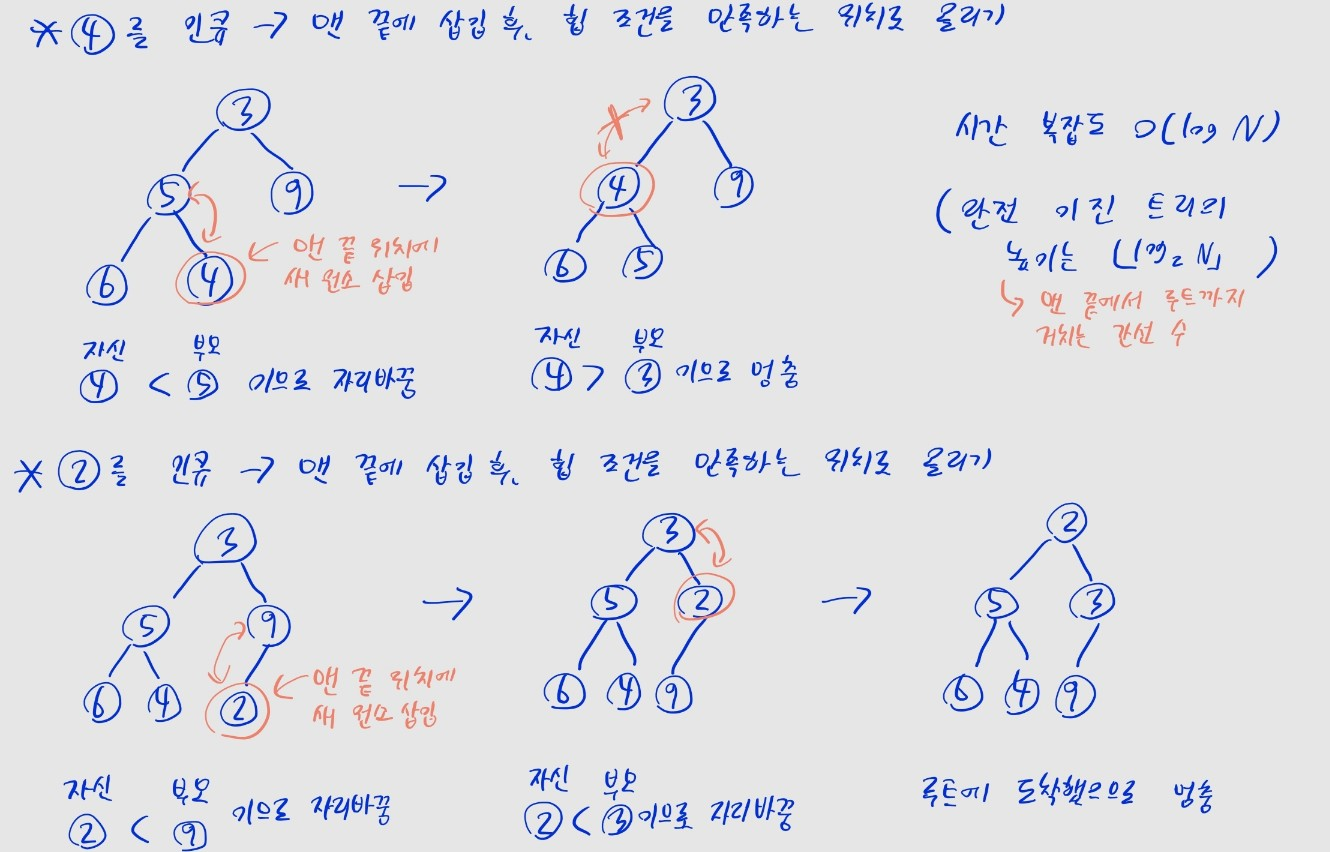
• (1) 원소를 완전 이진 트리의 맨 끝 위치에 추가
• (2) 삽입한 노드를, 힙 조건을 만족하는 위치로 올려 보냄
  • 부모 노드보다 자신의 값이 더 작은 경우, 부모와 위치를 교환
  • 루트 노드에 도착했거나, 더 이상 자신이 부모 노드보다 작지 않을 때까지 반복
• 원소가 $N$개일 때 시간 복잡도 $O(\log N)$
  • 완전 이진트리의 높이가 $\lfloor\log N\rfloor$이기 때문
  • 루트에서 맨 아래까지 내려가는 경우, 이진트리의 높이만큼 내려가게 됨
  • $\lfloor x \rfloor$는 $x$의 값을 내림한 정수를 뜻함

디큐 (힙에서 팝)

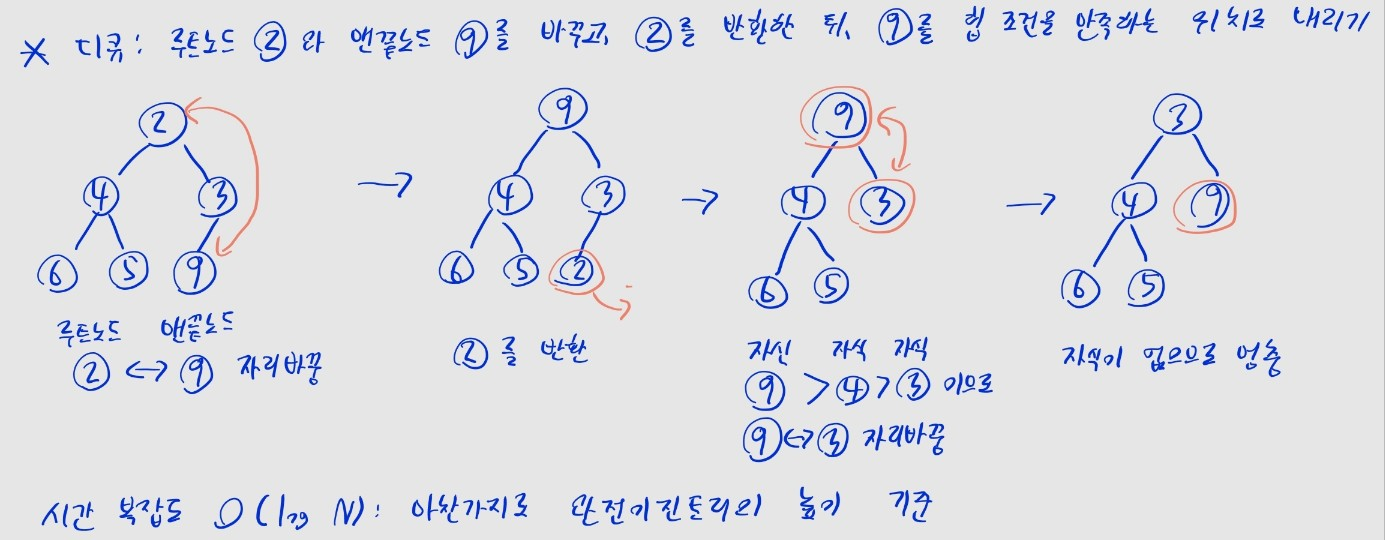
• (1) 루트 노드와 맨끝 노드의 자리를 바꿈
• (2) (원래 루트였던) 맨끝 노드를 반환
• (3) (원래 맨끝이였던) 루트 노드를, 힙 조건을 만족하는 위치로 내려 보냄
  • 자식 노드 중 자신의 값보다 작은 노드가 있으면, 그 중 가장 작은 자식과 위치를 교환
  • 자식이 없거나, 더 이상 자식 노드가 자신보다 작지 않을 때까지 반복
• 원소가 $N$개일 때 시간 복잡도는 마찬가지로 $O(\log N)$
  • 맨 아래부터 루트까지 올라가는 경우, 이진트리의 높이만큼 올라가게 됨

힙 정렬

• 원소 $N$개를 차례로 힙에 푸시하고, 차례로 팝한 값을 나열하면 정렬됨
  • 팝할 때마다 최솟값(또는 최대값)이 루트 노드를 반환하기 때문
• 힙에서 $N$번 팝을 수행하므로 $O(N \log N)$
• 힙 정렬에 대한 자세한 설명은 본 글 참조
  • 단 위 글은 최소 힙이 아니라 최대 힙 기준으로 설명해서, 사소하게 다른 내용이 있을 수 있음

heapq 모듈

최소 힙

• 인큐 / 힙 푸시: heapq.heappush(리스트, 값)으로 리스트에 값을 인큐
• 디큐 / 힙 팝: heapq.heappop(리스트)로 리스트의 가장 작은 값을 디큐
  • heapq 모듈은 최소 힙 기반
• 다음에 디큐될 원소 확인하기: 리스트[0]
  • 리스트의 원소는 최소 힙의 조건을 만족하도록 자동으로 위치가 변하기 때문에, 첫 값은 무조건 최소값
• 시간 복잡도: 인큐, 디큐 모두 $O(\log N)$
• 주의할 점: heappush나 heappop을 사용한 리스트에 .append(), .pop() 등 기존 리스트 메서드를 사용하면, 리스트의 힙 구조가 깨져 정상적으로 작동하지 않음

import heapq
heap = []
heapq.heappush(heap, 3)
heapq.heappush(heap, 1)
heapq.heappush(heap, 5)
print(heap[0])			   # 1
print(heapq.heappop(heap)) # 1
print(heapq.heappop(heap)) # 3
print(heapq.heappop(heap)) # 5

최대 힙

• 최대값을 가장 먼저 디큐하고 싶을 때는,
• heapq.heappush로 값에 -를 붙이고, heapq.heappop의 반환값에 다시 -를 붙이면 구현 가능

import heapq

def max_heappush(heap, x):
    heapq.heappush(heap, -x)

def max_heappop(heap):
    return -heapq.heappop(heap)

heap = []
max_heappush(heap, 3)     # 실제론 -3 푸시
max_heappush(heap, 1)     # 실제론 -1 푸시
max_heappush(heap, 5)     # 실제론 -5 푸시
print(heapq.heappop(heap)) # -(-5) = 5
print(heapq.heappop(heap)) # -(-3) = 3
print(heapq.heappop(heap)) # -(-3) = 1

기존 리스트를 최소 힙으로 바꾸기

• heapq.heappush()로 값을 추가한 리스트가 아닌, 기존의 리스트의 경우 바로 heapq.heappop()을 사용할 수 없음
  • 리스트가 최소 힙 구조를 만족하지 않기 때문
• heapq.heapify()로 리스트가 최소 힙 구조를 만족하게 변환한 뒤, heappush(), heappop()을 정상적으로 사용 가능

import heapq

a = [9, 5, 2, 7]

# heappop을 바로 사용하면 안 됨
print(heapq.heappop(a))  # 9 (가장 작은 값이 아님!!)

b = [9, 5, 2, 7]
# heapq.heapify를 이용해, 최소 힙 구조로 바꿔야 함
heapq.heapify(b)
print(heapq.heappop(b))  # 2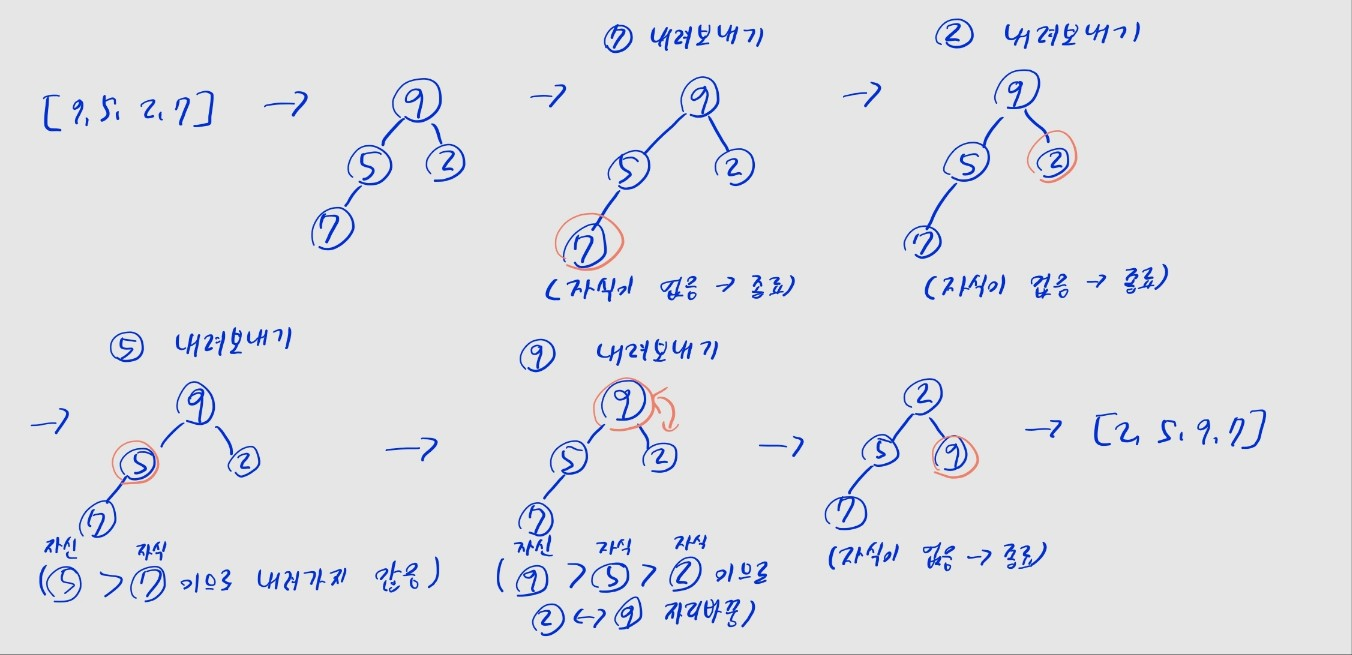

• heapq.heapify()의 시간 복잡도는 $O(N)$
• 내부적으로 트리의 아래쪽 노드부터 역순으로, 최소 힙 규칙을 만족하는 위치로 내려보내는 작업을 반복
  • 겉보기엔 노드별로 $O(\log N)$만큼 걸려 $O(N \log N)$ 같지만,
  • 노드가 하단에 있을수록 이동 경로가 짧으므로, 연산량의 합은 $O(N)$으로 수렴된다고 함

우선순위와 값을 쌍으로 인큐하기

• 튜플을 heappush하면, 기본적으로 튜플의 첫번째 원소 기준으로 정렬됨
• 즉 (우선순위, 값)의 형태로 인큐 및 디큐할 수 있음

import heapq

schedule = []
heapq.heappush(schedule, (4, "시험공부 하기"))
heapq.heappush(schedule, (1, "아이브 컴백 기념 뮤비 보기"))
heapq.heappush(schedule, (3, "한숨 자고 오기"))
heapq.heappush(schedule, (2, "배고프니 치킨 시켜먹기"))


print("<< 오늘의 일처리 순서 >>")
while schedule:
    print(heapq.heappop(schedule)[1])

# << 오늘의 일처리 순서 >>
# 아이브 컴백 기념 뮤비 보기
# 배고프니 치킨 시켜먹기
# 한숨 자고 오기
# 시험공부 하기

힙 정렬 구현

import heapq

def heapsort(array):
    result = []

    # 기존 리스트를 최소 힙으로 변경
    heapq.heapify(array)

    # 모든 원소를 차례대로 디큐
    while array:
        result.append(heapq.heappop(array))
    return result

array = [17, 4, 8, 9, 6]
print(heapsort(array))  # [4, 6, 8, 9, 17]

• 시간 복잡도는 $O(N)$ (heapify) + $O(N \log N)$ ($N$번 heappop) = $O(N \log N)$