수강신청을 할 때는 선이수 과목을 모두 이수했는지 확인하는 것이 중요해요!

위상 정렬에서도 선행 조건을 지키며 작업의 순서를 결정하게 됩니다.

위상 정렬

• 순서가 있는 작업을 순서에 맞춰 정렬하는 알고리즘
• 즉, 방향성 그래프에서 순서를 지키며 모든 노드를 순서대로 나열하는 것
  • 단, 그래프에는 사이클이 없어야 함
• 특정 노드를 방문하기 위해선, 해당 노드를 가리키는 이전의 모든 노드를 먼저 방문해야 함

진입차수, 진출차수

• 진입차수 (indegree): 특정 노드로 들어오는 간선의 개수
• 진출차수 (outdegree): 특정 노드에서 나가는 간선의 개수
• 특정 노드를 방문하기 위해선, 해당 노드를 가리키는 이전의 모든 노드를 먼저 방문해야 함
  • 즉, 진입차수가 0이 되어야 함

큐를 이용한 위상 정렬

• (1) 진입차수가 0인 모든 노드를 큐에 삽입

• (2) 큐가 빌 때까지 다음 과정을 반복
  • 큐에서 원소를 꺼내, 해당 노드에서 나가는 간선을 그래프에서 제거
  • 새롭게 진입차수가 0이 된 모든 노드를 큐에 삽입
  • 일반적으론 번호가 낮은 노드부터 삽입

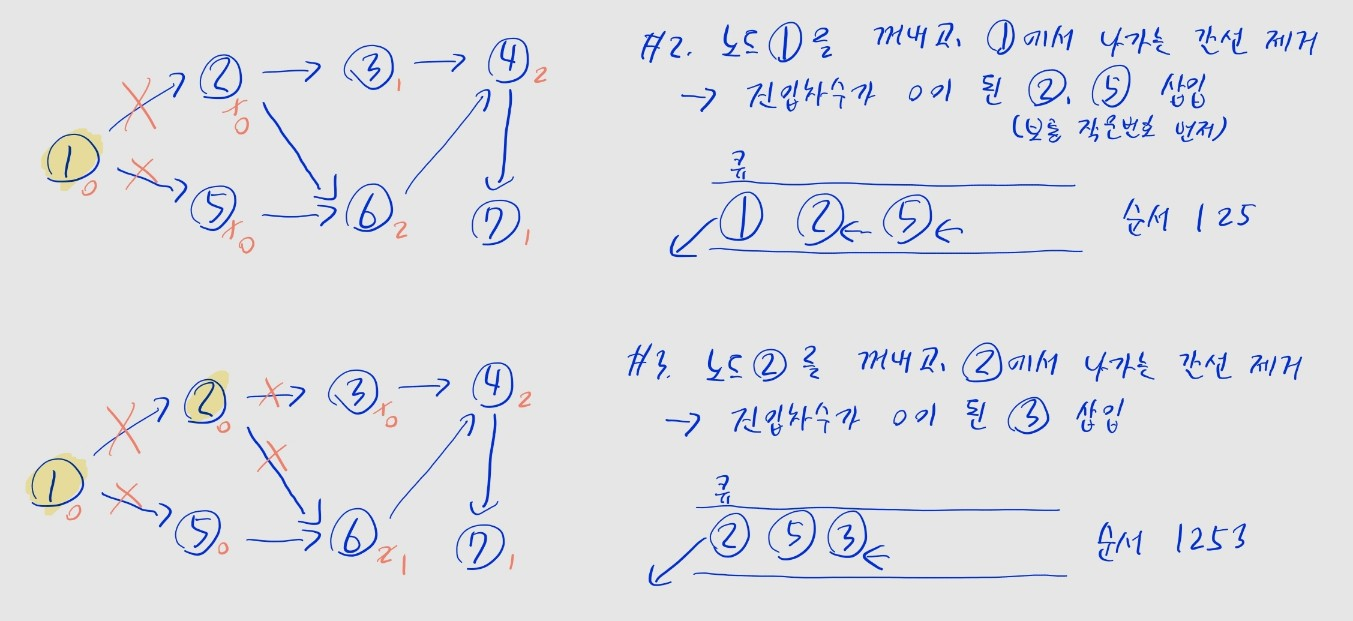
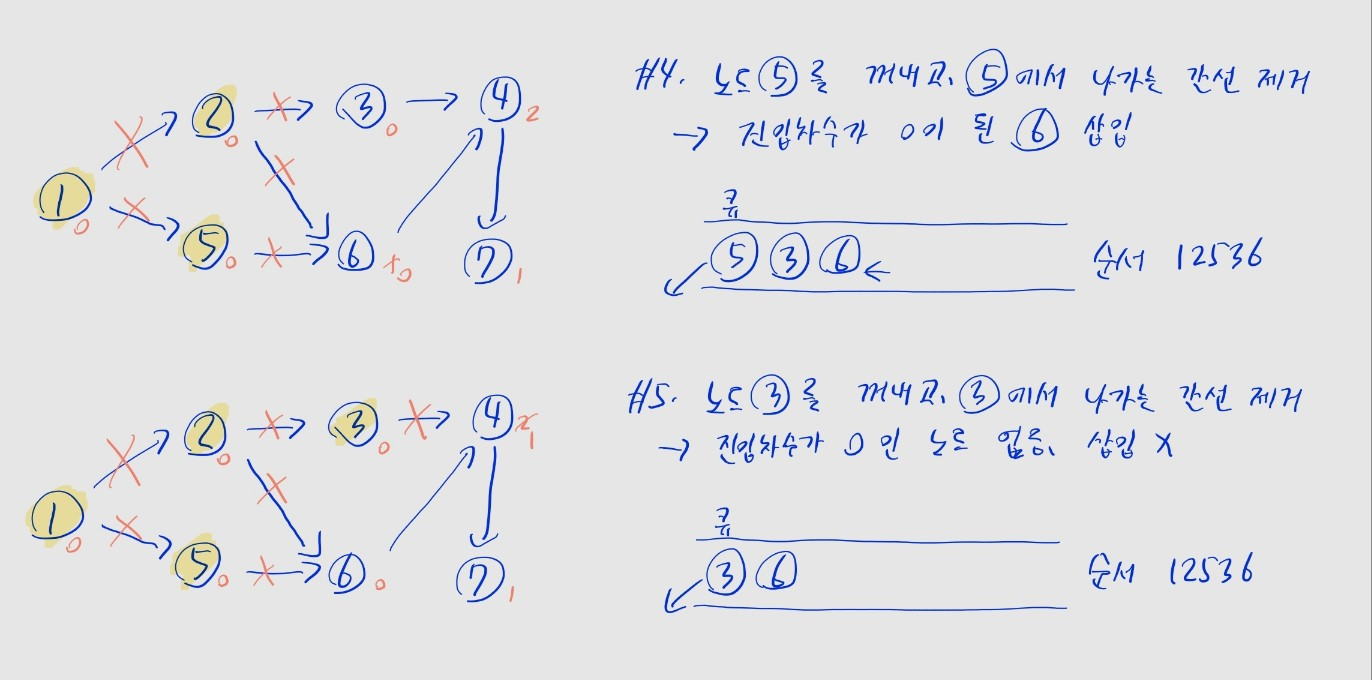
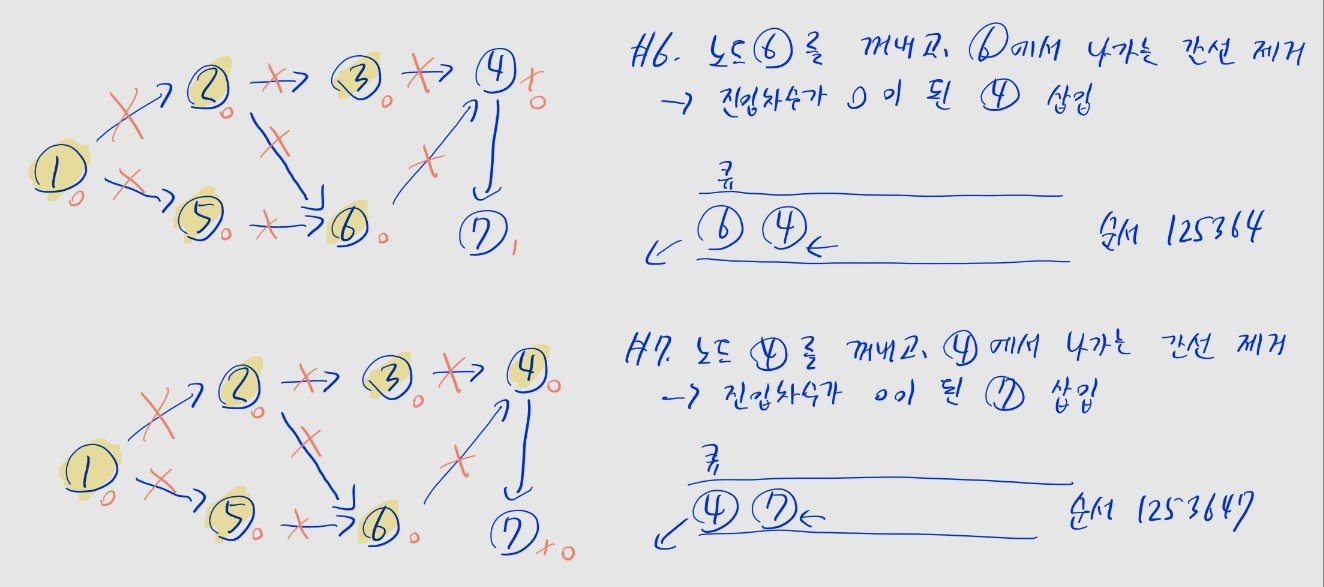
• (3) 각 노드가 큐에 삽입된 순서가, 위상 정렬의 결과
  • 위 예제에선 1 -> 2 -> 5 -> 3 -> 6 -> 4 -> 7

• cf. 모든 원소를 방문하기 전에 큐가 빈다면, 사이클이 존재한다고 판단할 수 있음
  • 사이클에 포함된 모든 원소는 큐에 들어갈 수 없기 때문

구현

from collections import deque

N = 7 # 노드의 수

# 연결 리스트: 각 노드에 연결된 간선 정보
graph = [
    [],
    [2, 5],
    [3, 6],
    [4],
    [7],
    [6],
    [4],
    []
]

# 각 노드의 진입 차수 계산
indegree = [0] * (N + 1)
for i in range(1, N + 1):
    for j in graph[i]:
        indegree[j] += 1

• 각 노드의 진입 차수를 indegree 리스트로 관리

# 위상 정렬
def top_sort():
    result = []         # 정렬 결과
    queue = deque()

    # 진입차수가 0인 노드 삽입
    for i in range(1, N + 1):
        if indegree[i] == 0:
            queue.append(i)

    # 큐가 빌 때까지
    while queue:
        # 노드를 꺼내고
        curr = queue.popleft()
        result.append(curr)
        # 노드에서 꺼내는 간선을 제거
        for i in graph[curr]:
            indegree[i] -= 1
            # 진입차수가 0이 된 경우 삽입
            if indegree[i] == 0:
                queue.append(i)

    # 결과 출력
    for i in result:
        print(i, end=" ")

top_sort() # 1 2 5 3 6 4 7

• 큐에서 노드를 꺼내고, 노드에서 나가는 간선을 제거하는 작업 반복
• 인접 리스트에서 간선을 직접 제거할 필요는 없고, indegree 리스트의 값만 1 감소시켜주면 됨

시간 복잡돔

• 차례대로 모든 노드를 확인하며, 모든 간선을 제거
• 노드가 $N$개 간선이 $E$개일 때 $O(N + E)$

문제풀이

2252. 줄 세우기

백준 / 골드 3 / 2252. 줄 세우기

• 각 학생을 그래프의 노드로 표현하면,
• 학생 A가 학생 B의 앞에 서야 한다: 노드 A -> B 방향의 간선이 존재한다
• 위와 같은 형태의 그래프에서 위상 정렬을 하면 쉽게 풀리는 문제

• cf. 오른쪽처럼 그래프의 모든 노드가 연결되어 있지 않다고 해도, 위상 정렬은 가능함에 유의

from collections import deque
import sys

input = sys.stdin.readline

N, M = map(int, input().split())
graph = [[] for _ in range(N + 1)]
indegree = [0] * (N + 1)

for _ in range(M):
    # 학생 A가 학생 B 앞에 서야 됨
    # 즉, 노드 A -> 노드 B 방향의 간선이 존재함
    
    a, b = map(int, input().split())
    graph[a].append(b)
    indegree[b] += 1
    
def topsort():
    queue = deque()
    
    for i in range(1, N + 1):
        if indegree[i] == 0:    
            queue.append(i)

    while queue:
        curr = queue.popleft()
        print(curr, end=" ")
        for i in graph[curr]:
            indegree[i] -= 1
            if indegree[i] == 0:
                queue.append(i)                    

topsort()