자동완성 기능과 유사하게 동작하는 트라이와, 실제 데이터베이스에서도 사용되는 B 트리를 알아봅시다람쥐. 🐿️

트라이

• 문자열 검색에 특화된 트리 기반의 자료구조
• 각 문자를 노드로 저장해 연결 -> 문자열 앞부분만 보고 저장 여부를 빠르게 파악 가능
• 앞 글자를 치면 원하는 단어가 뜨는 자동완성을 생각하면 됨

트라이의 구조

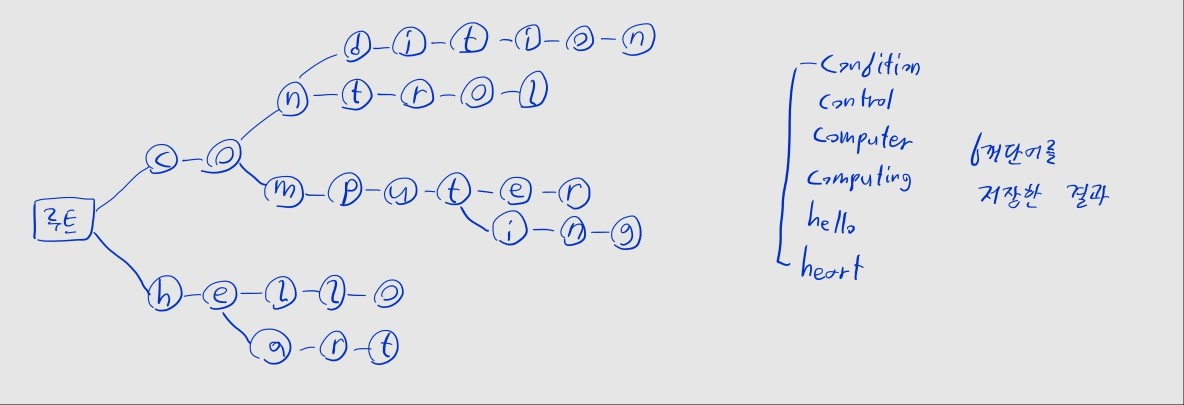
• 문자열의 각 문자를 순서대로 트리의 노드에 저장
• 자식 노드는 다음에 올 수 있는 문자를 나타냄
• 동일한 접두어를 공유하는 문자열은, 해당 글자의 노드들을 공유하므로 중복 저장을 줄일 수 있음
  • e.g., computer, computing의 c, o, m, p, u, t는 동일 노드로 관리됨
• 루트 노드(문자열의 시작)에는 문자 값이 없음에 유의

시간 복잡도

• 찾는 단어의 길이가 $N$일 때, 각 글자를 한 글자씩 확인하는 과정에서 $O(N)$.
• 트라이에 단어가 몇 개 저장되어 있든, 시간 복잡도는 $O(N)$

🤔 왜 굳이 해시 테이블(집합) 말고 트라이를 쓰나요? 문자열들을 집합에 저장해 두면, 탐색에 필요한 시간 복잡도는 $O(1)$ 아닌가요?

• 트라이의 가장 큰 장점은 접두어 기반 검색이 간편하다는 점입니다.
• 예를 들어 comp로 시작하는 모든 단어를 찾고 싶다면, 집합에선 모든 단어를 일일이 확인해서 comp로 시작해야 하는지 확인해야 합니다.
• 반면 트라이에서는 노드 c, o, m, p를 따라간 뒤, 그 아래 하위 트리만 탐색하면 쉽게 단어들을 찾을 수 있습니다.
• 또한 단어들이 접두어를 많이 공유할수록, 해시 테이블보다 트라이가 공간 효율적이라는 장점도 있습니다.

구현

• 클래스를 이용해서 트라이를 직접 만들어 봅시다.

# 각 노드를 나타내는 클래스
class Node:
    def __init__(self):
        self.children = {}
        # {문자: 노드 객체} 꼴
        self.end = False    # 단어의 마지막 글자인가?

class Trie:
    def __init__(self):
        self.root = Node()
    # 이후 코드에 계속

• Node: 각 노드를 나타내는 클래스
  • self.children은 노드의 자식 노드를 저장
    • {'A': 자식노드 객체, 'C': 자식노드 객체...} 꼴
  • self.end는 해당 노드가 문자열의 마지막 문자인지 여부 저장
    • 문자열이 트라이에 존재하는지 확인할 때 필요
• Trie: 트라이를 나타내는 클래스
  • self.root엔 루트 노드를 저장
  • 루트 노드에는 문자 값이 없고, 자식만 존재

🤔 end 속성은 왜 필요한가요?

• 접두어가 동일한 여러 개의 단어를 함께 저장할 때 필요합니다.

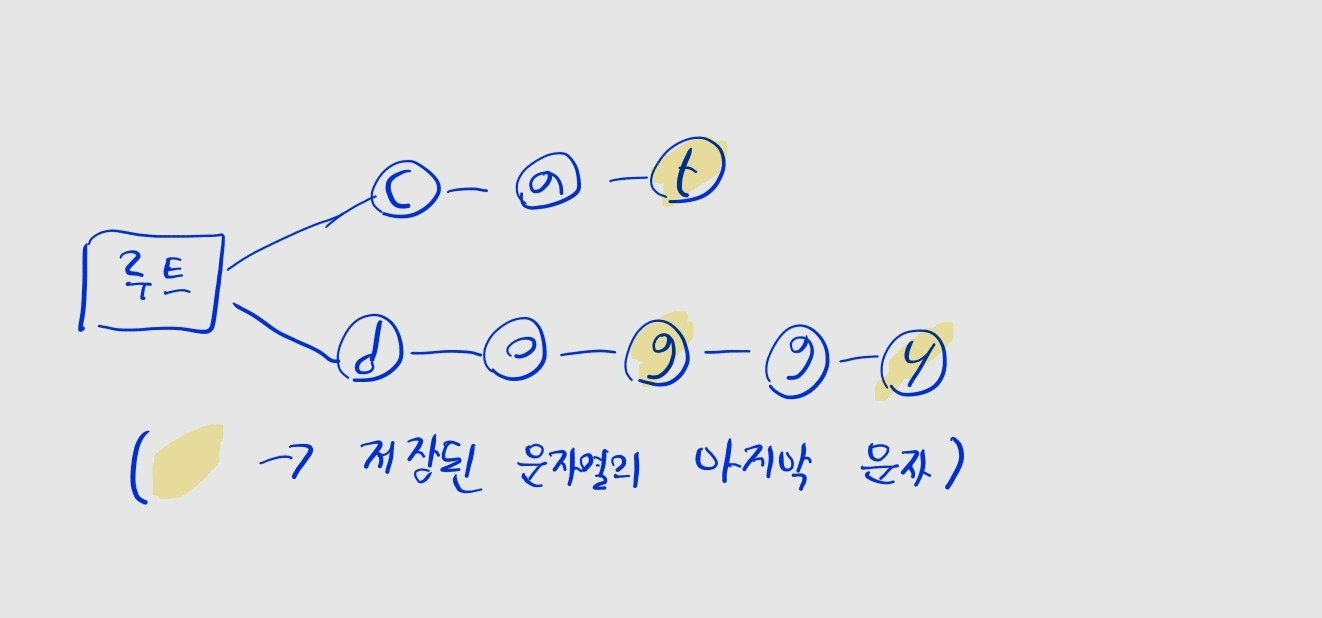
• 위 사진의 트라이에는 dog, doggy가 모두 저장되어 있습니다.
• 이때 g(dog의 마지막 문자)와 y(doggy의 마지막 문자) 모두 end 속성을 True로 지정해서, 두 단어가 모두 저장되어 있음을 나타낼 수 있습니다.

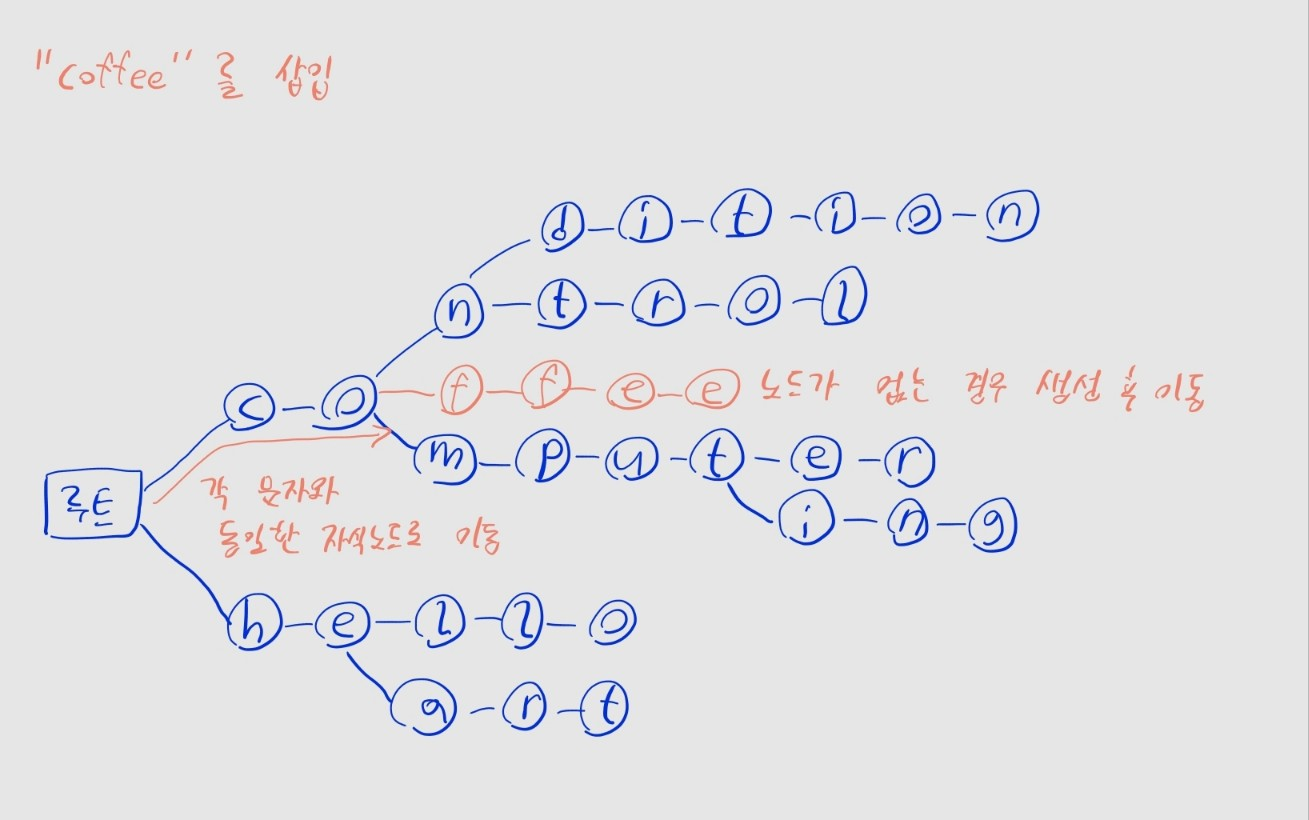
문자열 삽입

• 루트 노드부터 시작
• 삽입할 문자열의 각 문자를 순차적으로 확인하며, 자식 노드 중에 존재하는지 확인
  • 존재하면, 해당 자식 노드로 이동
  • 존재하지 않으면, 노드를 생성한 뒤 이동
• 마지막 문자를 삽입한 이후, 노드의 end 속성을 True로 설정

# class Trie: 계속
# 문자열 삽입
def insert(self, word):
    curr = self.root    # 현재 노드

    # 문자열의 각 글자가
    # 현재 노드의 자식 중에 존재하는지 확인
    for char in word:
        # 없으면 해당 노드를 생성
        if char not in curr.children:
            curr.children[char] = Node()
        curr = curr.children[char]
    curr.end = True

문자열 검색

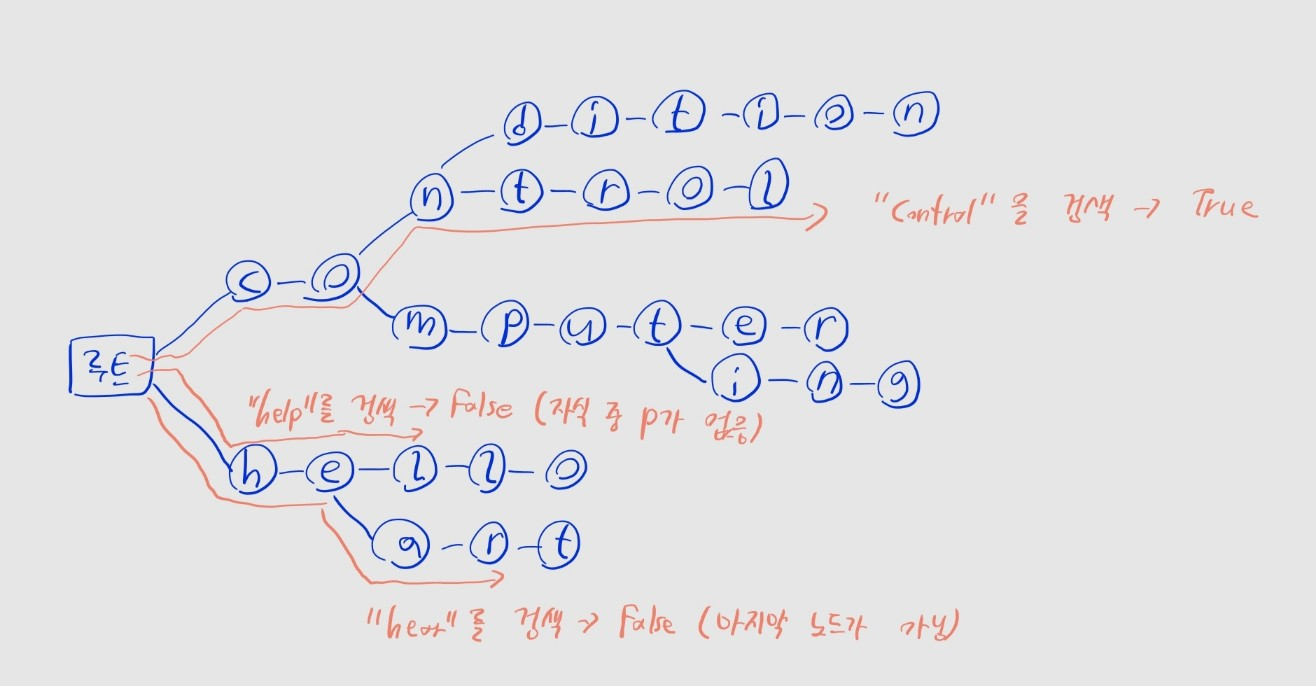
• 검색할 문자열의 각 문자를 순차적으로 확인하며, 자식 노드 중에 존재하는지 확인
  • 존재하면, 해당 자식 노드로 이동
  • 존재하지 않으면, False 반환
• 마지막 문자까지 탐색한 후, 현재 노드의 end 속성값을 반환해 존재 여부 확인

# class Trie: 계속
# 찾기 메서드
def search(self, word):
    curr = self.root
    for char in word:
        if char not in curr.children:
            return False
        curr = curr.children[char]
    return curr.end

🤔 위 그림의 트라이에서 comp라는 단어를 삽입하고 싶어요. 그런데 이미 computer가 들어 있는데 가능한가요?

• 가능합니다. c -> o -> m -> p까지 이동한 다음에, p 노드의 end 속성을 True로 바꿔주면 됩니다.
• 그러면 search 메서드로 comp를 찾을 때도, 마지막 노드 p의 end 속성이 True이므로 True를 반환합니다.

특정 접두어로 시작하는 문자열을 모두 검색

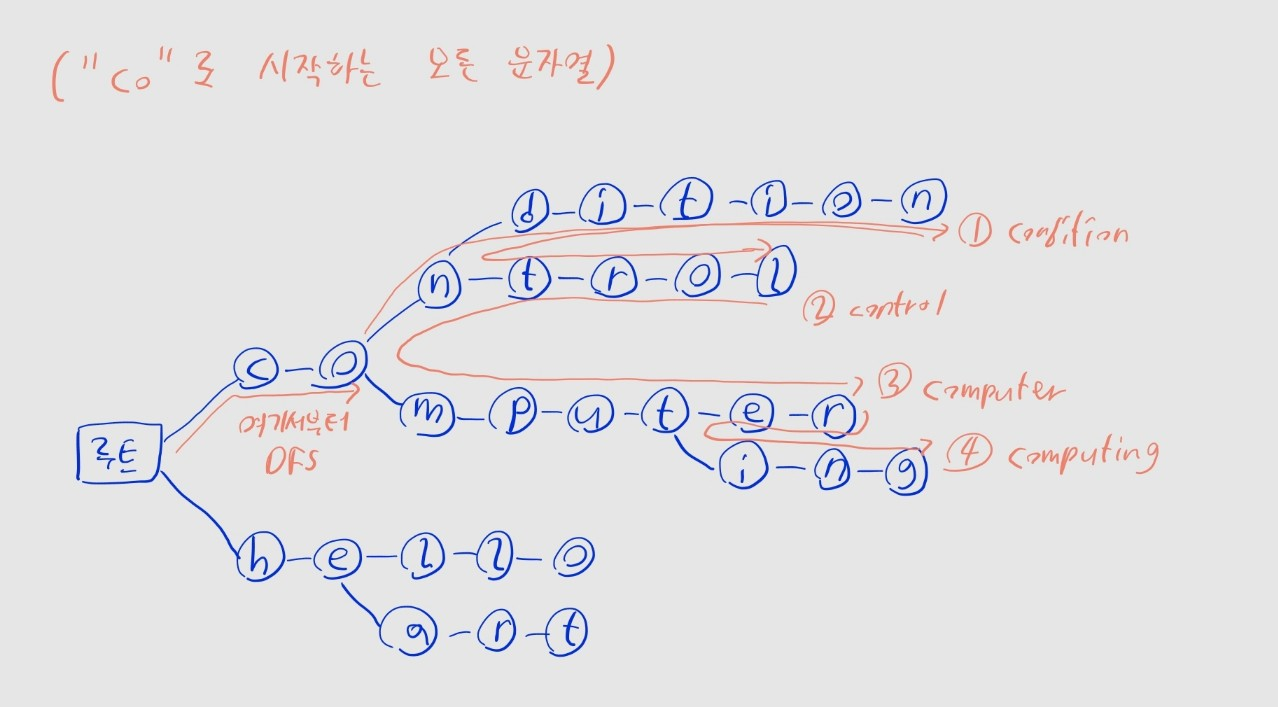
condition도 탐색해야 했는데 빠뜨렸군요. 용서해주세요...

• starts_with는 검색할 접두어 prefix의 각 문자를 순차적으로 따라가며, 마지막 문자의 노드까지 이동
  • 현재 트라이에 접두어가 존재하지 않는 경우, 빈 리스트를 반환
• 접두어의 마지막 노드까지 도달한 경우
  • 해당 노드를 시작점으로 _dfs 메서드를 재귀호출하면서 DFS를 수행
  • 탐색 경로에 따라 prefix 매개변수에 현재 노드의 문자를 추가하며 단어를 구성
  • end에 도달하면, 현재까지 구성한 단어를 words 배열에 추가해 리턴
• 최종적으로 접두어로 시작하는 모든 단어를 리스트로 반환하게 됨

# class Trie: 계속
# 해당 접두어로 시작?
def starts_with(self, prefix):
	node = self.root
    	# 접수어의 마지막 노드까지 이동
        for char in prefix:
            if char not in node.children:
                return []  # 접두어가 없음
            node = node.children[char]
        # BFS 수행
        return self._dfs(prefix, node)

    def _dfs(self, prefix, node):
        words = []
        if node.end:				# 단어를 완성했을 때 words에 단어 추가
            words.append(prefix)
        
        # 이후 재귀 호출에서 찾은 모든 단어들의 리스트를 words에 extend
        for char, next_node in node.children.items():	# 자식 노드 재귀호출
            words.extend(self._dfs(prefix + char, next_node))
        return words

삭제

• 삭제는 분량 상 구현은 생략합니다.
• cat, dog, doggy가 저장된 트라이가 있다고 가정했을 때...
• 우선 문자열을 삭제하려면 존재 여부를 파악해야 하니, 해당 노드까지 이동해야 함
• (1) cat을 삭제하는 경우
  • cat과 동일한 접두어를 가진 문자열이 없으므로, t -> a -> c 순으로 삭제
• (2) dog을 삭제하는 경우
  • dog은 doggy의 접두어이므로, g의 end 속성만 False로 바꾸고, 노드는 삭제하지 않음
• (3) doggy를 삭제하는 경우
  • dog까지 삭제하면 안 되므로, y -> g 순으로 삭제

동작 확인

trie = Trie()
trie.insert("condition")
trie.insert("control")
trie.insert("hello")
trie.insert("heart")
print(trie.search("control"))       # True
print(trie.search("controller"))    # False
print(trie.starts_with("he"))       # ["hello", "heart]

B 트리

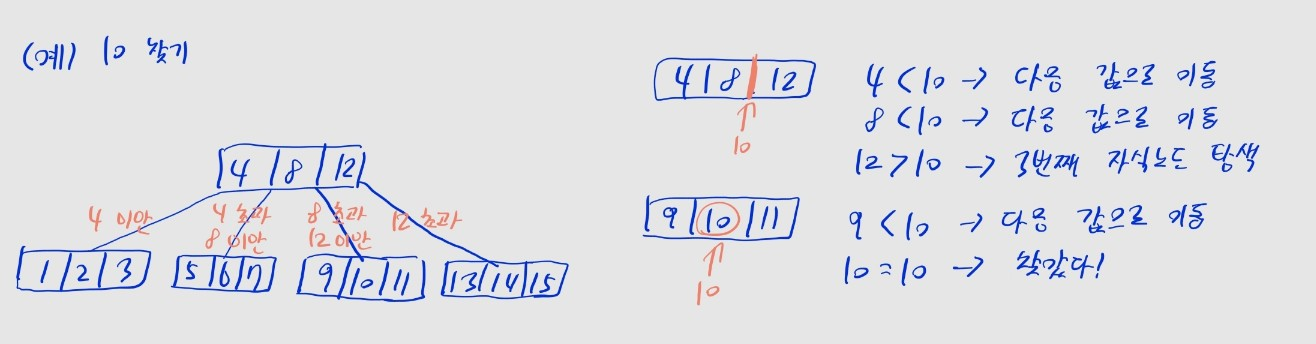
• 노드에 여러 값을 저장할 수 있는 트리
  • 배열의 형태로 여러 값이 저장됨
• 차수 (최대 자식 수) $m$을 사전에 정해 둠
  • 위 사진에선 $m = 4$
• 각 노드는 최대 $m-1$개의 키를 가지며, 키 값들은 오름차순 정렬되어 있음
• 노드의 양끝 및 각 값 사이에는 자식 노드 존재
  • 각 자식 노드는 왼쪽 부모보다 크고, 오른쪽 부모보다 작은 값을 포함
  • 위 사진의 루트 노드에선, $4$ 미만, $4$ 초과 $8$ 미만, $8$ 초과 $12$ 미만, $12$ 초과로 자식이 나뉨
• 차수가 $m$인 B-트리를 $(m-1)$ - $(m)$ 트리라고도 함
  • 사진의 트리는 $3$-$4$ 트리

B 트리 vs 이진탐색트리

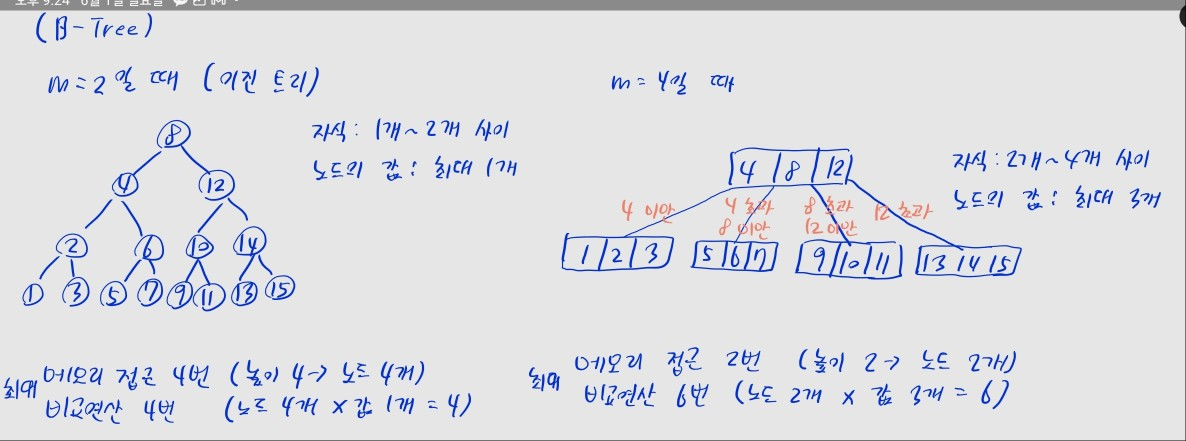
• 이진탐색트리는 $m=2$인 B트리로 볼 수 있음
• $m$이 증가할수록 메모리 접근 횟수는 줄어듦
  • 이유: 트리의 높이가 낮아져, 값을 찾을 때 거쳐야 하는 노드 수가 줄어듦
• $m$이 증가할수록 비교 연산 횟수는 많아짐
  • 이유: 한 노드에서 더 많은 값을 비교해야, 찾는 값의 위치를 확인할 수 있음
• 보통 디스크 접근 비용이 큰 데이터베이스(SQL 등)에서 B 트리 기반 자료구조를 사용

B+ 트리

• 실제 데이터는 리프 노드(데이터 노드)에만 저장되어 있음
• 상위 노드(인덱스 노드)에는 값 비교를 위한 기준값만 저장되어 있음
  • 즉, 무조건 리프 노드까지 내려가야 함
• 각 리프 노드는 이중 연결 리스트 구조로 연결되어 있음
  • 범위를 지정하고 값을 찾을 때 유용
  • e.g., 3 이상의 값 찾기 -> 3부터 8까지 매번 루트 노드부터 탐색할 필요 없음
  • 최솟값인 3을 먼저 찾고, 연결 리스트를 통해 나머지 값을 탐색할 수 있음
• 범위 검색의 장점 때문에, 데이터베이스에서는 B트리보단 B+ 트리를 주로 사용