수학쌤이 말합니다. “오늘 몇일이지? 24일? 24번, 나와서 문제 풀어봐.”

굳이 학생들을 줄 세워서 한명씩 번호를 확인할 필요는 없죠.

이게 바로 해시 테이블의 원리입니다.

해시법

• 데이터를 저장할 위치 (인덱스)를 간단한 연산으로 구하는 방법

배열 (list)의 단점

• 값을 지정해 원소를 찾는 데 $O(N)$이 걸림
• 선형 탐색: 원하는 원소를 찾을 때까지, 첫 값부터 차례대로 비교

# 5를 찾기
a = [1, 2, 3, 4, 5]
for i in range(len(a)):
    if a[i] == 5:
        print(i)

• 특정 값이 배열에 존재하는지 확인할 때 (x in list)도 선형 탐색으로 동작 -> $O(N)$
• 이걸 더 빨리 할 수 있는 자료구조는 없을까? -> 해시 테이블

해시 테이블

• 키: 데이터를 식별하는 고유한 값
• 해시 함수: 키를 해시코드로 변환하는 함수
  • e.g., 키를 13으로 나눈 나머지 ($h(x) = x \mod 13$. mod 는 나머지 연산 기호임)
• 해시 테이블: 해시코드를 인덱스로 사용해, 키를 저장하는 배열 구조
  • e.g., 키가 17일 때, $17 \mod 13 = 4$이므로 17은 4번째 인덱스에 저장됨
• 버킷: 해시 테이블의 각 인덱스 공간
• 즉 해시 함수는 키로부터 인덱스를 계산해서, 데이터를 빠르게 저장하거나 검색할 수 있게 함

• 키의 존재 여부 확인: 키를 해시코드로 바꿔주고, 해당 인덱스 위치를 확인하면 끝!
  • e.g., 20 찾기: $20 \mod 13 = 7$ -> 해시 테이블의 7번째 원소가 20인지 확인하면 끝
  • 배열처럼 모든 값을 차례로 확인할 필요가 없음
• 새로운 키를 삽입/삭제: 키를 해시코드로 바꿔주고, 해당 인덱스 위치에 값을 삽입/삭제하면 끝!
  • e.g., 35 삽입: $35 \mod 13 = 9$ -> 해시 테이블의 9번째 원소에 35를 삽입하면 끝

키, 값 쌍

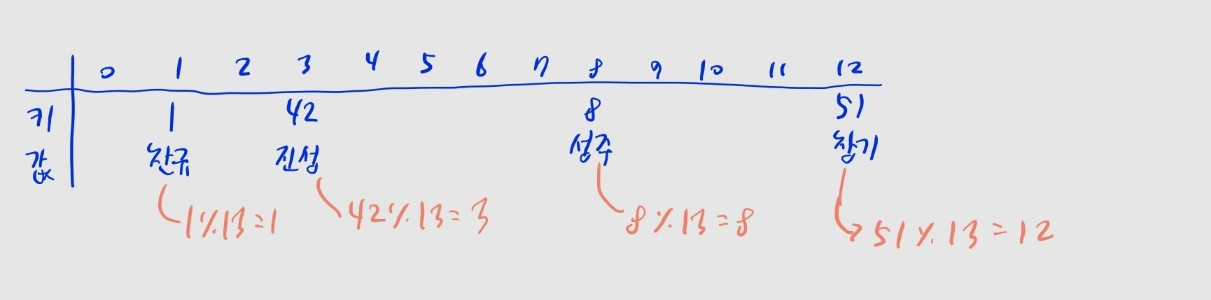
• 보통은 키와 값 쌍을 저장함
  • 키: 데이터를 식별하는 고유한 값으로, 중복될 수 없음. 해시코드를 구하는 데 사용됨
  • 값: 키에 대응되는 데이터로, 중복될 수 있음
  • e.g., (키: 1, 값: 찬규)은 1번 인덱스에 저장됨. $1 \mod 13 = 1$
  • e.g., (키: 51, 값: 창기)는 12번 인덱스에 저장됨. $51 \mod 13 = 12$

• 키는 무조건 존재해야 하며, 값은 없어도 됨
  • 이하 예제부턴 키만 다루고, 값은 생략
• 파이썬의 dict형은 키와 값이 함께 저장된 해시 테이블, set형은 키만 저장된 해시 테이블

🤔 해시 테이블에서는 키 간 순서가 존재하나요?

• 아뇨, 해시 테이블에서는 원소 간 순서가 존재하지 않습니다.
• 즉 정렬 같은 용도로 활용하려면 해시 테이블이 아니라 배열 (파이썬 list)을 사용해야 합니다.
• 따라서 탐색 과정에도 특정 키의 순서를 반환하지 않습니다. 탐색은 키의 존재 여부 및 키에 대응되는 값을 반환하는 연산이라고 생각하면 됩니다.

🤔 키는 숫자로만 지정할 수 있나요?

• 숫자 말고 문자열 등 다른 자료형으로도 지정할 수 있습니다.
• 대신 문자열 등 자료형에 따라 다른 해시 함수가 적용될 수 있습니다.
• 파이썬 기준으로는 이뮤터블 자료형(int, float, str, tuple)만 키로 지정할 수 있고, 뮤터블 자료형(list 등)은 지정할 수 없습니다.
• 대신 값은 어떤 자료형으로든 저장할 수 있습니다.

해시 충돌

• 2개 이상의 키가 동일한 해시코드를 가져, 저장할 버킷이 중복되는 현상
  • e.g., $h(x) = x \mod 13$일 때, $5 \mod 13$과 $18 \mod 13$ 모두 5
  • 키 $5$가 5번 인덱스에 저장된 상황에서 키 $13$을 삽입하려고 할 때 충돌 발생
• 2가지 방법으로 해결 가능
  • 체인법 (오픈 해시법): 해시코드가 같은 원소들을 연결 리스트에서 관리
  • 오픈 주소법: 빈 버킷을 찾을 때까지 새로운 해시코드를 계산해, 다른 인덱스에 삽입 시도

🤔 지금 해시함수 $x \mod 13$는 0부터 12까지의 정수만 반환하지 않나요? 해시 충돌이 너무 자주 발생할 것 같은데요.

• $x \mod 13$은 예제일 뿐이고, 실제 해시 테이블에서는 훨씬 더 복잡한 해시 함수를 사용합니다. 특히 파이썬의 dict와 set는 비트 연산이나 랜덤 값 추가 등을 사용한 복잡한 해시 함수를 사용한다고 합니다. 반환 가능한 값의 범위도 훨씬 넓습니다.

체인법

• 해시코드가 같은 노드를 연결 리스트로 관리

키를 탐색할 때

• (1단계) 해시 함수를 사용해, 키를 해시코드로 변환
• (2단계) 해당 인덱스의 연결 리스트를 스캔하며, 검색할 노드를 탐색
• (3단계) 스캔 중 같은 키가 발견되면 탐색 성공, 끝까지 스캔했는데 못 발견하면 실패

• 시간 복잡도
  • 평균 $O(1 + \alpha)$ ($\alpha = \frac{N}{M}$)
  • $\alpha$(부하도): $N$은 전체 원소 수, $M$은 버킷 수 -> 버킷에 저장된 평균 원소 수
  • 탐색 과정에서 연결 리스트의 각 키를 순차 탐색해야 함, 부하도가 높을수록 오래 걸림
  • 모든 키가 한 인덱스에 몰리는 최악의 경우 $O(N)$

키를 삽입할 때

• 연결 리스트의 꼬리가 아닌 머리에 삽입함
  • 꼬리에 삽입하면 이전 노드를 모두 거쳐야 하므로, 더 빠른 머리 삽입 사용
• (1단계) 해시 함수를 사용해, 키를 해시코드로 변환
• (2단계) 해당 인덱스의 연결 리스트를 스캔하며, 중복되는 키가 있는지 확인
  • 중복값이 있으면 삽입 실패
• (3단계) 중복값이 없는 경우, 연결 리스트 맨 앞에 노드 추가

• 시간 복잡도
  • 중복 키 탐색 과정에서 평균 $O(1 + \alpha)$, 최악 $O(N)$

키를 삭제할 때

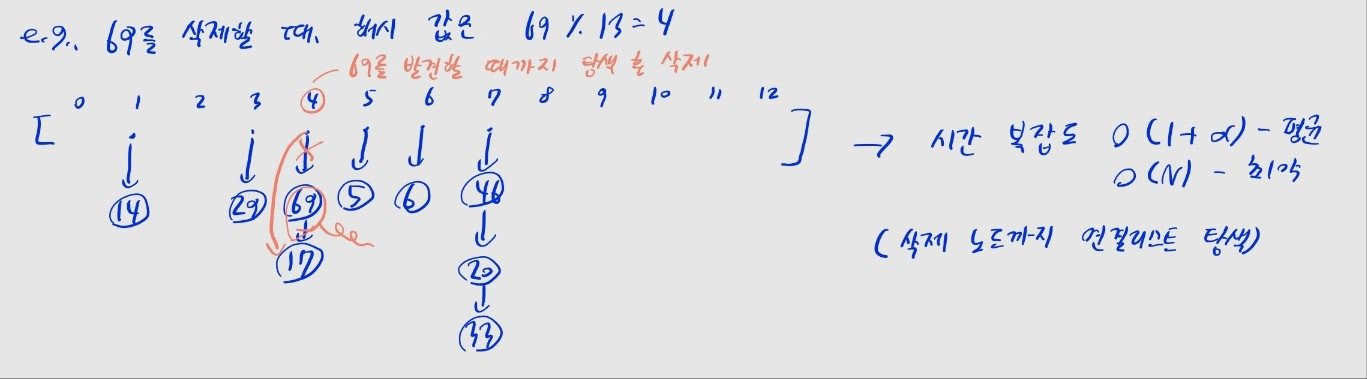
• (1단계) 해시 함수를 사용해, 키 (원소의 값)를 해시코드로 변환
• (2단계) 해당 인덱스의 연결 리스트를 스캔하며, 삭제할 노드를 탐색
• (3단계) 노드를 발견하면 해당 노드를 리스트에서 삭제

• 시간 복잡도
  • 중복 키 탐색 과정에서 평균 $O(1 + \alpha)$, 최악 $O(N)$

오픈 주소법

• 충돌이 발생했을 때, 새로운 해시코드를 구해 (재해시) 빈 버킷을 찾기
• e.g., 선형 탐사법
  • 충돌이 발생한 기존 해시코드를 $h$로 둘 때,
  • 새 해시코드 $r(x) = (h + 1)$ (바로 다음 버킷) 시도

키를 삽입할 때

• 키를 해시 코드로 전환하고, 해당 버킷에 삽입하기
• 충돌이 발생한 경우, 계속해서 새 해시코드를 구해 다음 노드 시도

• 시간 복잡도
  • 평균 $O(1 / (1 - \alpha))$ ($\alpha = \frac{N}{M}$), 최악 $O(N)$
  • 대충 부하도 $\alpha$ 높을수록 충돌도 많이 발생해, 탐색에 더 오래 걸린다 정도로만 이해하기
  • 모든 키의 해시 코드가 동일한 최악의 경우, 재해시가 $N$번까지 이루어지므로 $O(N)$

키를 탐색할 때

• 각 버킷은 다음과 같은 속성을 가짐
  • 현재 데이터가 저장되어 있음 (숫자)
  • 비어 있음 - 데이터가 있었는데 삭제됨 (★)
  • 비어 있음 - 한번도 데이터가 저장된 적 없음 (-)

• 키를 해시 코드로 전환하고, 해당 버킷의 값 확인
  • 값이 ★거나, 찾는 키와 해시 테이블의 키가 다를 때
    • 데이터가 저장됐던 적이 있는 칸 -> 찾는 키가 이 칸에서 충돌됐을 수 있음, 재해시를 한 뒤 다른 칸을 확인해야 함
  • 값이 -일 때
    • 한번도 데이터가 저장된 적 없는 칸 -> 충돌이 발생했을 수 없음, 찾는 키는 테이블에 없음

• 시간 복잡도
  • 평균 $O(1 / (1 - \alpha))$ ($\alpha = \frac{N}{M}$), 최악 $O(N)$
  • 대충 부하도 $\alpha$가 높을수록 충돌도 많이 발생해, 탐색에 더 오래 걸린다 정도로만 이해하기

키를 삭제할 때

• 삭제하려는 키를 원소를 탐색할 때와 같은 방법으로 탐색한 후, 삭제
• 삭제한 다음엔 버킷에 삭제가 완료됐음을 명시해야 함 (★)

• 시간 복잡도
  • 평균 $O(1 / (1 - \alpha))$ ($\alpha = \frac{N}{M}$), 최악 $O(N)$
  • 대충 부하도 $\alpha$ 높을수록 충돌도 많이 발생해, 탐색에 더 오래 걸린다 정도로만 이해하기

파이썬의 set, dict

• 파이썬의 set, dict는 해시 테이블을 이용해서 구현됨
• 충돌 방지 방법으로는 오픈 주소법 사용
• set, dict는 부하도 $\alpha$가 일정 값 이상이 되면, 자동으로 크기가 더 큰 해시 테이블로 확장됨
  • 즉 탐색, 삽입, 삭제 연산의 시간 복잡도는 $O(1)$라고 생각해도 됨

dict: 키, 값이 저장된 해시테이블

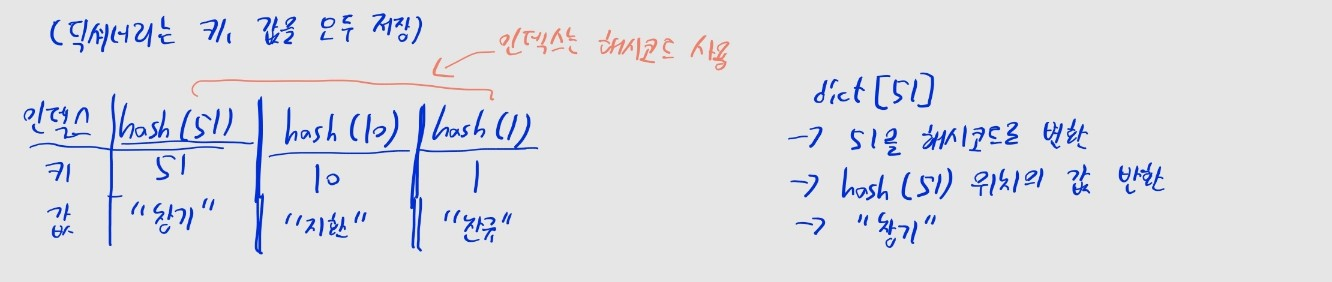
• 키와 값을 함께 해시 테이블에 저장하는 방식으로 구현
• e.g., a = {51: "창기", 10: "지환", 1: "찬규"}일 때, 51, 10, 1이 해시 테이블의 키
  • 키는 중복값을 허용하지 않으므로, dict의 키도 중복될 수 없음
• a[51]: 키가 51인 데이터 탐색, 시간 복잡도 $O(1)$
  • 실제론 51을 해시코드로 변환하고, 해당 위치에 저장된 값을 반환
• a[8] = "성주": 키가 8, 값이 "성주"인 데이터 삽입, 시간 복잡도 $O(1)$
• a.pop(10): 키가 10인 원소 삭제하기, 시간 복잡도 $O(1)$
• 해시 테이블은 순서가 없지만, Python 3.7부턴 dict는 삽입 순서를 유지하도록 구현됨
  • for key in dict 등 반복문 사용 시, 정해진 순서대로 반환됨

set: 키만 저장된 해시테이블

• 키만 저장하고 값은 저장하지 않음
  • 정확히는 값은 None 처리
• e.g., a = {1, 2, 3}의 1, 2, 3은 모두 키
  • 키는 중복값을 허용하지 않으므로, set 역시 중복값을 저장할 수 없음
• 1 in a: 원소 탐색하기, 시간 복잡도 $O(1)$
  • 실제론 1을 해시코드로 변환하고, 해당 위치에 값이 저장되었는지 반환
• a.add(4): 원소 삽입하기, 시간 복잡도 $O(1)$
• a.remove(5)): 원소 삭제하기, 시간 복잡도 $O(1)$