행렬 너무 어렵습니다. 정석으로 복습하고 오겠습니다.

생각해봅시다!

• 굉장히 시간제한이 빡빡한 문제입니다. Python 3 말고 PyPy로 푸는 걸 추천합니다.
  • 전 결국엔 Python 3로 풀어냈는데... 좀 변태같은 최적화가 필요해서 힘겨웠습니다.
• 결국에는 이 문제도 동적계획법 문제입니다. 문제의 모든 행렬을 다 곱하기 전에, 일부 행렬만 곱해둔 값을 저장해 두고 활용해야 합니다.
• 점화식이 쉽게 떠오를 리가 없지. 심지어 백준에서는 테스트 케이스도 짤막한 거 하나만 줬지... 천천히 따라와봅시다.

입력

import sys
input = sys.stdin.readline

N = int(input())
sizes = [tuple(map(int, input().split())) for _ in range(N)]

memo = [[0] * (N) for _ in range(N)]

• N에 행렬의 수를 입력받습니다.
• 리스트 sizes에 각 행렬의 크기를 (행의 수, 열의 수) 형태로 입력받습니다.

DP 테이블 정의하기

• 2차원 리스트 memo를 정의합니다. memo[i][j]에는 sizes[i]부터 sizes[j]까지의 행렬을 곱할 때 필요한 곱셈 연산 횟수의 최솟값을 저장합니다.
  • i, j는 0부터 N - 1까지의 인덱스를 가지며, 행렬 곱의 순서를 유지해야 하므로 항상 i ≤ j입니다. 따라서 memo의 아래쪽 절반은 사용하지 않습니다.

기저 조건

• i == j인 경우,sizes의 i번째부터 i번째 행렬까지 행렬곱을 구하게 되는데... 당연히 행렬이 하나뿐이므로 곱할 게 없습니다.
• 따라서 i == j일 땐 memo[i][j] = 0이 됩니다.

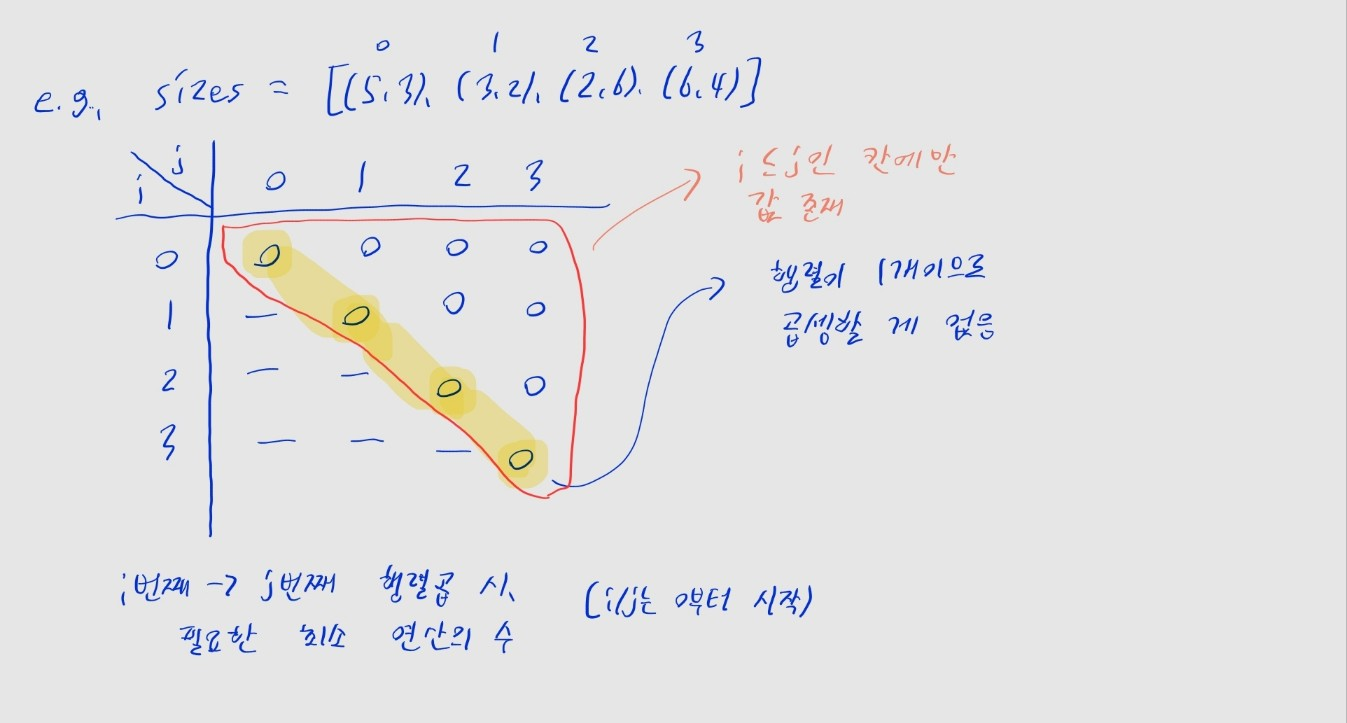
경우 나누기

• 이제 memo[i][j]의 값을 구하는 방법을 생각해 봅시다.
  • 예를 들어, 행렬 $A, B, C, D, E$가 존재할 때, 다섯 행렬을 곱했을 때 필요한 최소 곱셈 횟수를 구하고 싶다고 합니다.
  • 그러면 첫 행렬 (0번째) $A$부터 마지막 행렬 (4번째) $E$까지 곱하게 되니까,memo[0][4]의 값을 구해야겠죠.
• 이때 전체 행렬 곱셈을 네가지 방식으로 나눌 수 있습니다.
  • $A(BCDE)$: $A$와 $BCDE$를 따로 곱한 뒤, 두 결과를 마지막에 곱해주기
  • $(AB)(CDE)$: $AB$와 $CDE$를 각각 구한 뒤, 두 결과를 마지막에 곱해주기
  • $(ABC)(DE)$: $ABC$와 $DE$를 각각 구한 뒤, 두 결과를 마지막에 곱해주기
  • $(ABCD)E$: $ABCD$와 $E$를 각각 구한 뒤, 두 결과를 마지막에 곱해주기
  • 이 네가지 경우 중에서 연산 횟수가 가장 적은 방법이 답이 됩니다.

# 아직 완성된 코드는 아님

for k in range(i, j):
	memo[i][k]	 # i번째 ~ k번째 행렬까지 곱함. 이걸 써먹어야 함
    memo[k+1][j] # k+1번째 ~ j번째 행렬까지 곱함. 이걸 써먹어야 함

• 코드에선 경우를 나눌 때, $i \leq k < j$인 변수 $k$를 둡니다.
  • $i$번째 ~ $k$번째 행렬끼리 곱해주고, $k+1$번째 ~ $j$번째 행렬까지 곱해주는 거죠.
  • 위 예제에선 $i = 0, j = 4$이므로 $0 \leq k < 4$의 값을 가질 수 있습니다.
  • e.g., k = 2일 땐 0 ~ 2번째 $ABC$를, 3 ~ 4번째 $DE$를 각각 구하고, 두 결과를 다시 곱합니다.

구해야 하는 값

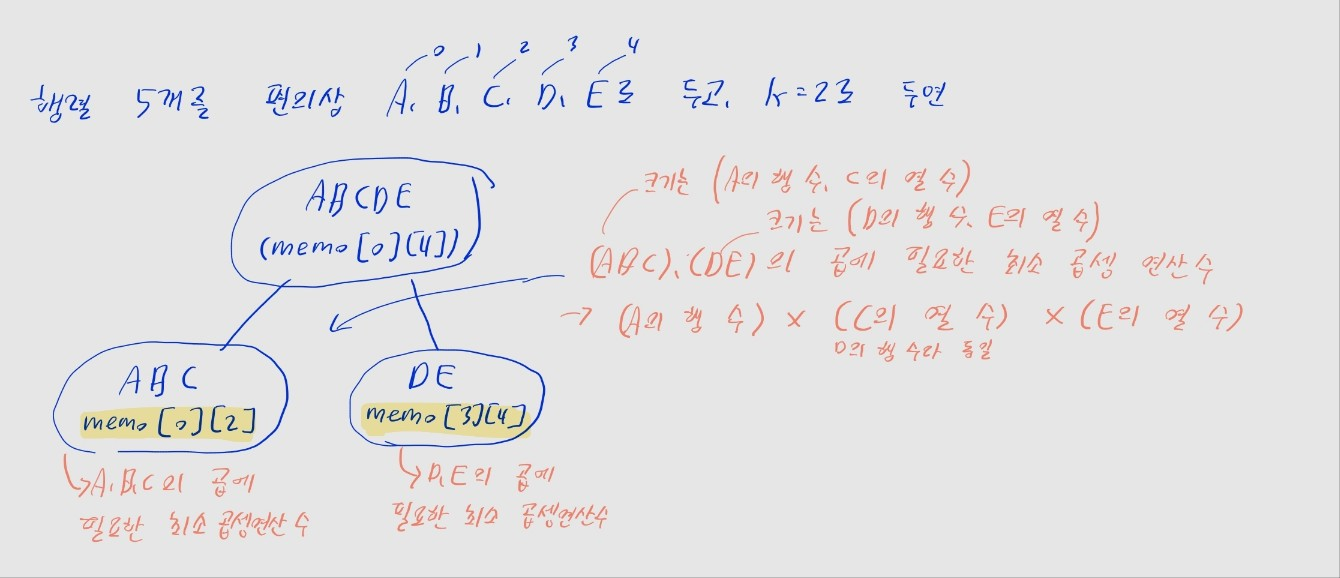
• 최종적으로는 아래 세 값을 다 더하면, $i$번째~$j$번째 행렬끼리 곱했을 때 총 곱셈 횟수를 구할 수 있습니다.
  • (1) $i$-$k$번째 행렬끼리 곱했을 때의 최소 곱셈 횟수 (이건 memo[i][k]겠죠?)
  • (2) $k+1$-$j$번째 행렬끼리 곱했을 때의 최소 곱셈 횟수 (이건 memo[k+1][j]겠죠?)
  • (3) 위에서 곱한 결과인 두 행렬을 다시 곱했을 때 곱셈 횟수

행렬곱의 연산횟수

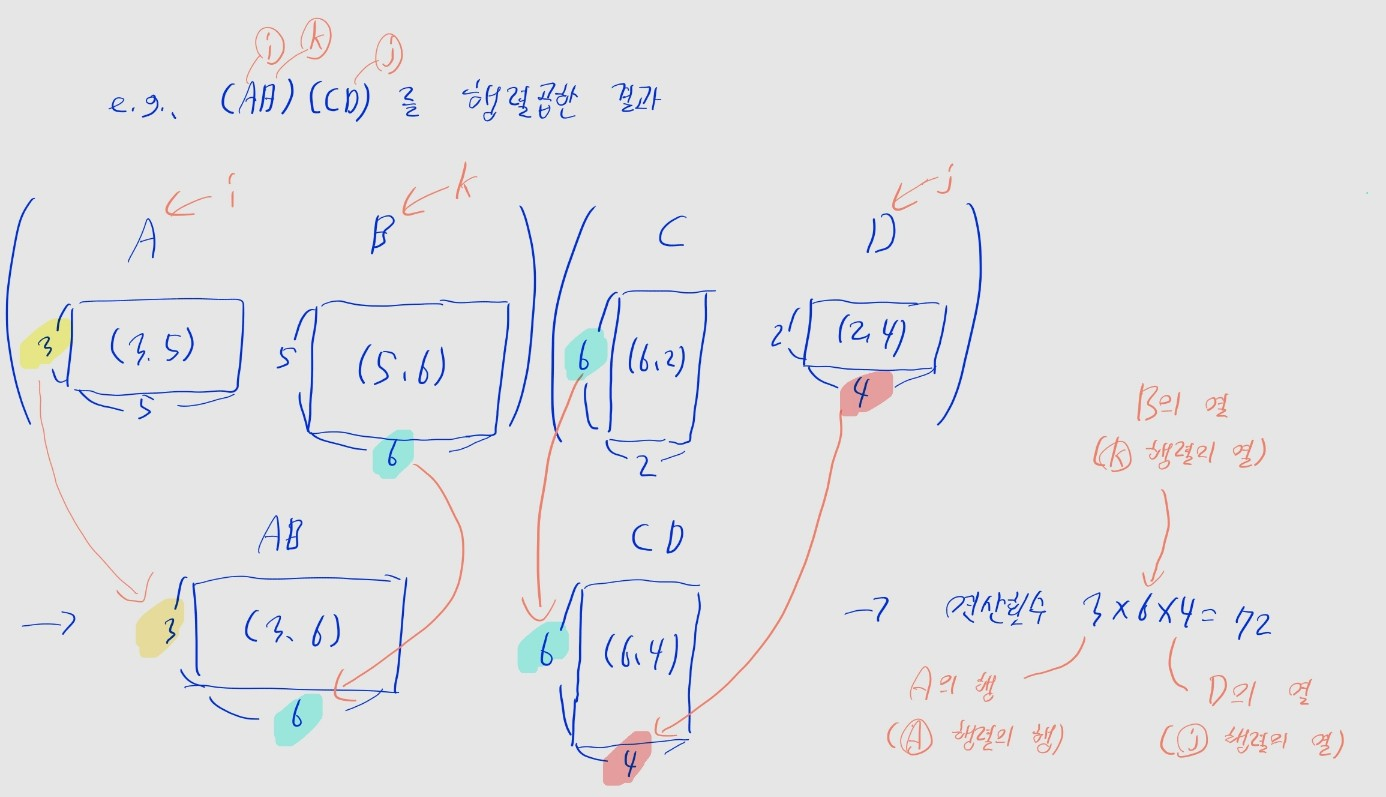
제발 외웁시다. (행이 X개, 열이 Y개) 크기인 행렬을 (행이 Y개, 열이 Z개)인 행렬과 곱하면, 행렬의 크기는 (행이 X개, 열이 Z개)가 됩니다. 제발~~

• (3)은 어떻게 계산할 수 있을까요?
• i번째~k번째 행렬을 곱한 행렬의 크기는
  • (i번째 행렬의 행 수, k번째 행렬의 열 수)가 됩니다.
• k+1번째~j번째 행렬을 곱한 행렬의 크기는
  • (k+1번째 행렬의 행 수, j번째 행렬의 열 수)가 됩니다.
• 이때 k번째 행렬의 열 수와 k+1번째 행렬의 행 수는 동일합니다.
• 즉 곱셈 횟수는 (i번째 행렬의 행 수) * (k번째 행렬의 열 수) * (j번째 행렬의 열 수)로 구할 수 있습니다.
• 이는 sizes[i][0] * sizes[k][1] * sizes[j][1]로 계산합니다.

완성된 점화식

# 점화식 코드
temp = float('inf')	# 최솟값 갱신을 위한 초기 무한의 값
            
for k in range(i, j):
	cost = memo[i][k] + memo[k + 1][j] + sizes[i][0] * sizes[k][1] * sizes[j][1]               
	if cost < temp:
    	temp = cost
        
memo[i][j] = temp

• 이 값을 모두 더하면 memo[i][k] + memo[k+1][j] + sizes[i][0] * sizes[k][1] * sizes[j][1]가 됩니다.
• $i \leq k < j$ 범위의 모든 k에 대해 위 값을 계산한 뒤, 최솟값을 memo[i][j]에 저장합니다.

풀이

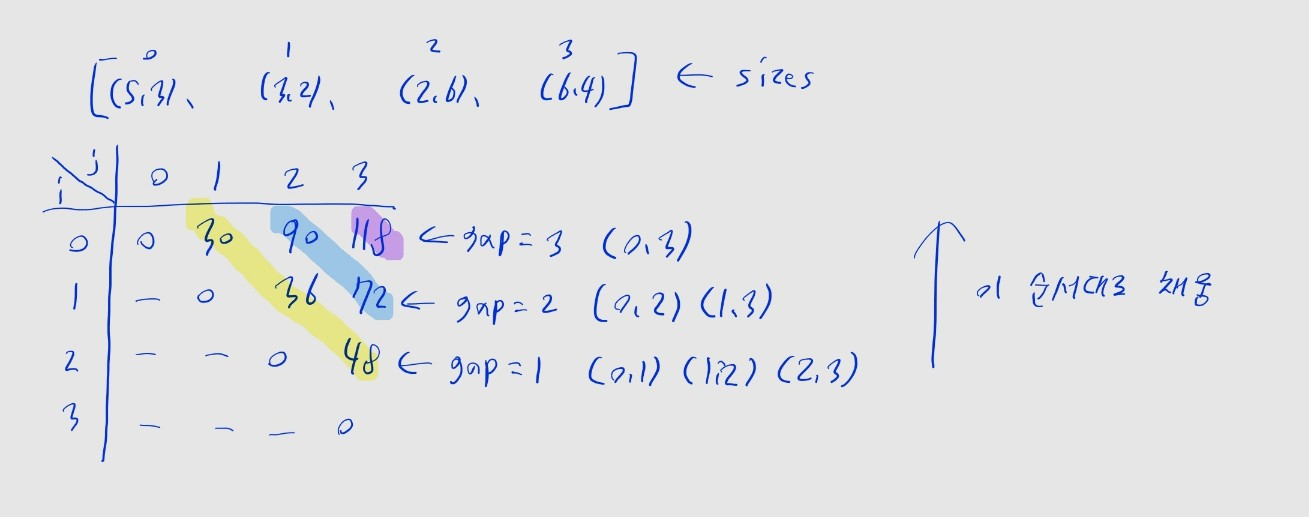
import sys
input = sys.stdin.readline

N = int(input())
sizes = [tuple(map(int, input().split())) for _ in range(N)]

memo = [[0] * (N) for _ in range(N)]

def find_answer():
    for gap in range(1, N):
        for i in range(N - gap):
            j = i + gap
            temp = float('inf')
            
            for k in range(i, j):
                cost = memo[i][k] + memo[k + 1][j] + sizes[i][0] * sizes[k][1] * sizes[j][1]
                
                if cost < temp:
                    temp = cost
            
            if i == 0 and j == (N - 1):
                return temp
            memo[i][j] = temp
                   
print(find_answer())

• DP 테이블은 곱하는 행렬이 1개 -> 2개 -> 3개 -> 4개....인 칸 순서대로 채워집니다.
  • 즉 j - i가 0, 1, 2, 3, ....인 칸 순서대로 채워집니다.
  • 위 코드에서는 gap = j - i이 작은 값부터 채워 나갑니다.
  • 이에 따라 DP 테이블도 오른쪽 위 방향으로 채워집니다. (그림 참고)
  • 이는 memo[i][j]를 계산하려면, 더 왼쪽 아래에 있는 memo[i][k], memo[k+1][j]가 먼저 채워져 있어야 하기 때문입니다.
• 본 코드에서는 i == 0 and j == (N - 1)일 때 DP 테이블 채우기를 멈추고 바로 답을 반환하게 설정했습니다.
  • 안 그러면 Python 3 기준 시간 초과가 뜨더군요. PyPy는 이렇게까지 안 해도 통과될 겁니다.

시간 복잡도

• 행렬의 수가 $N$개일 때, DP 테이블에는 $N + (N - 1) + (N - 2) +... + 2 + 1$ -> 약 $N^2$개 칸을 채워야 함
  • 각 칸을 채울때마다 for k in range(i, j)로 최대 $N$개의 k를 검사
• 최종 $O(N^3)$. $N \leq 500$이므로 $1,250,000$번 연산 필요. 1초 안에 가능!