백준 / 골드 4 / 2110. 공유기 설치

생각해봅시다!

• 이것도 모르면 맞아야지 스타일 문제. 해결법만 떠오르면 빠르게 풀 수 있는데, 그게 어려워요!
• 공유기를 설치할 집들을 정한 뒤, 공유기 사이 거리를 계산하는 건 어떨까요?
  • 문제는 집의 수 $N \leq 200,000$라는 점
  • 그 과정에서 시간초과가 뜰 겁니다... 아마 높은 확률로
• 도저히 풀이가 안 보이네요. 그런데 이럴 때일수록 발상을 "역전"해야 합니다.

• "공유기를 설치할 집들을 정한 뒤", "공유기 사이 거리를 계산한다" 가 아니라...
• "공유기 사이 거리를 먼저 정한 뒤", "그 거리로 설치가 가능한지를 확인한다"로 생각을 "역전"해 보는거죠!
• 물론 우리는 나루호도나 치히로가 아니라서 쉽게 안 떠오르는 게 맞습니다. 저도 푸는 데 2시간 걸렸습니다. GPT한테 힌트도 받았어요.

공유기 설치 가능 여부 확인

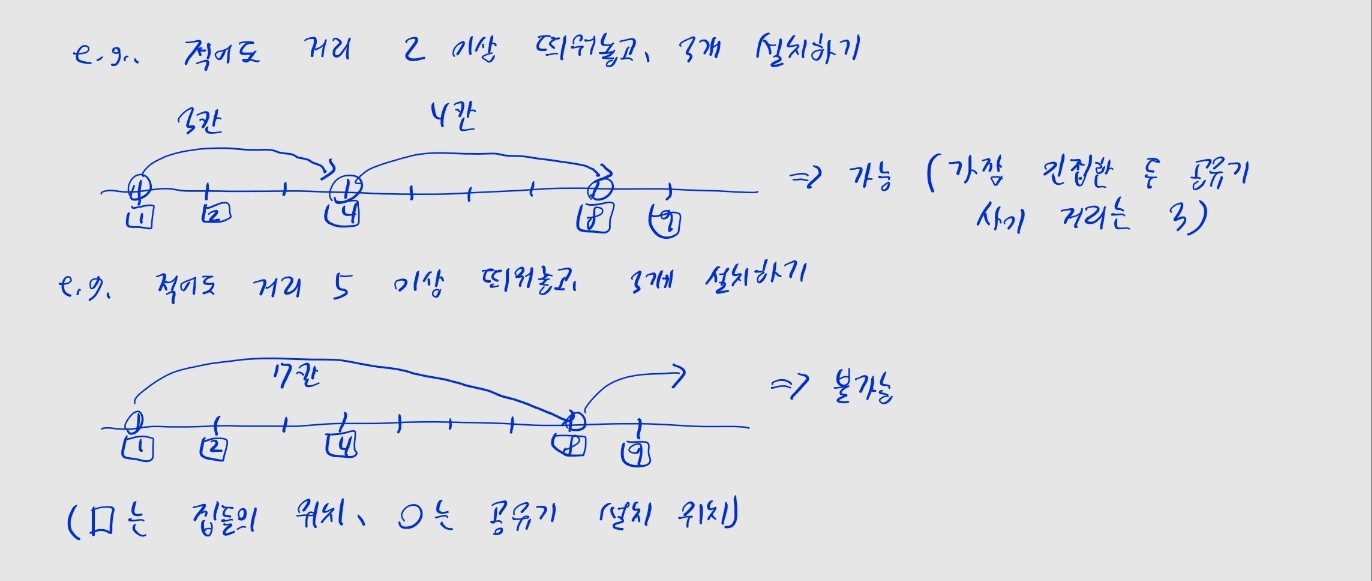
• 일단 우리는 공유기 간 거리를 가능한 떨어뜨려 놔야 합니다.
• "두 공유기 사이를 최소한 거리 $n$만큼 띄워놔야 한다" 하고 규칙을 정한 뒤,
• 이 규칙을 만족하며 $N$개 집에 $C$개의 공유기를 설치할 수 있는지 여부를 판단해봅시다.

이 점들을 유념합시다

• 첫번째 집에는 무조건 공유기를 설치합니다. 우리는 최대한 공유기를 벌려놔야 하는데, 첫 칸을 낭비하는 건 효율적이지 않겠죠.
• 최소 거리 $n$를 넓게 설정할수록, 조건을 만족하기 어렵습니다. 넓게 넓게 설치하려다가 공유기를 설치할 수 있는 집의 수가 부족해질 가능성이 큽니다.

N, C = map(int, input().split())

# 집들의 좌표 저장
houses = []

for _ in range(N):
    houses.append(int(input()))

# 좌표 정렬
houses.sort()

# 제일 인접한 거리가 n 이상이 되도록 c개를 설치 가능?
def can_build(n):
    # 첫 집에는 무조건 설치
    loc = houses[0]
    total = 1               # 설치한 공유기 수
    min_dist = float('inf') # 가장 인접한 두 공유기 간 위치
    
    # 나머지 C - 1개 설치
    for i in range(1, len(houses)):
        if houses[i] - loc >= n:
            total += 1
            min_dist = min(min_dist, houses[i] - loc)
            loc = houses[i]
            
            # C개를 다 설치한 경우, 제일 인접한 거리 반환
            if total == C:
                return min_dist

    # C개를 다 설치하지 못한 경우, 좁혀야 함
    return False 

can_build 함수를 만들어 봅시다

• can_build 함수는 두 공유기 사이의 거리가 최소 n 이상이 되도록 하며, C개의 공유기를 설치할 수 있는지 반환합니다.
• 첫번째 집에 공유기를 설치한 후, 이후엔 이전 공유기와의 거리가 n 이상인 집에만 설치합니다.
• 설치할 때마다 직전 공유기와의 거리를 구하며, 최솟값을 min_dist 변수로 갱신합니다.
  • 함수의 정상 실행을 위해, 입력받을 때 집들의 위치를 오름차순 정렬해야 합니다 (houses.sort())
• C개를 모두 설치할 수 있으면, min_dist 값을 반환합니다.
  • 이 값을 통해 "이 거리만큼은 떨어뜨려 설치할 수 있음"을 확인하게 됩니다.
• C개를 모두 설치하지 못한 경우, False를 반환합니다.
• 시간 복잡도는 $O(N)$ (for문으로 각 집을 1번씩 탐색하게 됩니다)

이분 탐색

• 네... 그렇습니다. 결국엔 이분 탐색으로 푸는 문제였습니다.
• 일단 정답인 가장 인접한 두 공유기 사이의 거리는 아래 범위에서 찾을 수 있을 겁니다.
  • 최솟값 left: 1 (양옆에 있는 집에 공유기가 설치된 경우)
  • 최댓값 right: 맨 뒷 집 좌표 - 맨 앞 집 좌표 (맨 앞 집, 맨 두 집 2군데에만 설치된 경우)
  • 그리고 이 범위의 값을 앞선 can_build 함수에 넣으면서 답을 찾습니다.
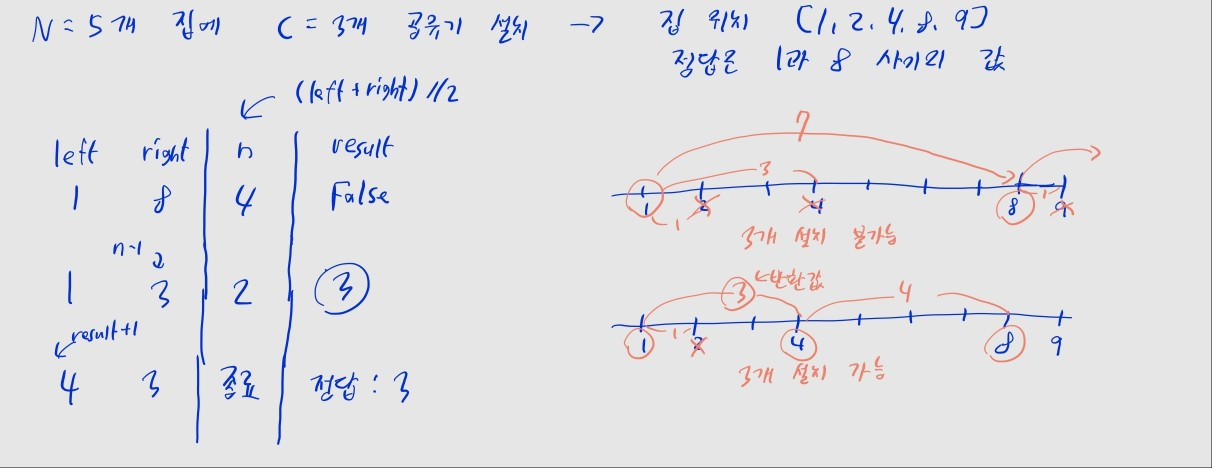
• 이때 $x_i \leq 1,000,000,000$이므로, 1부터 순서대로 can_build 함수에 넣다간 시간 초과가 뜹니다.
• 결국에는 이분 탐색으로 범위를 줄이며 답을 찾는 게 중요합니다.

# 이분탐색
def binary_search():
    left = 1
    right = houses[-1] - houses[0] # 정렬했던거 기억하죠?

    while left <= right:
        n = (left + right) // 2
        
        result = can_build(n)
            
        # 설치 가능: 일단 설치하고, 더 넓힐 수 있나 확인
        if result:
            answer = result
            left = result + 1
            
        # 설치 부가능: 더 줄여야 함
        else:
            right = n - 1
            
    return answer

• can_build가 False가 아닌 경우, 가장 인접한 두 공유기 사이 거리인 result를 반환.
  • 가장 인접한 두 공유기 사이 거리를 result로 두었을 때, 모든 공유기를 설치 가능하단 소립니다. (이때 n <= result 입니다)
  • 그런데 일단 정답의 최댓값을 계속 찾아봐야 합니다. result보다 거리를 더 늘려도, 설치가 가능할 수도 있잖아요.
  • 그래서 answer에 현재 result를 저장하고, left = result + 1로 설정해 result보다 더 큰 위치의 값을 찾아봅니다.
• can_build가 False인 경우,
  • 공유기를 다 설치할 수 없으니, 더 좁게 설치해야 합니다.
  • right = n - 1로 설정해, n보다 더 좁은 범위의 값을 찾아봅니다.

풀이

import sys

input = sys.stdin.readline

N, C = map(int, input().split())
houses = []

for _ in range(N):
    houses.append(int(input()))
    
houses.sort()

# 제일 인접한 거리가 n 이상이 되도록 c개를 설치 가능?
def can_build(n):
    # 첫 집에는 무조건 설치
    loc = houses[0]
    total = 1               # 설치한 공유기 수
    min_dist = float('inf') # 가장 인접한 두 공유기 간 위치
    
    # 나머지 C - 1개 설치
    for i in range(1, len(houses)):
        if houses[i] - loc >= n:
            total += 1
            min_dist = min(min_dist, houses[i] - loc)
            loc = houses[i]
            
            # C개를 다 설치한 경우, 제일 인접한 거리 반환
            if total == C:
                return min_dist

    # C개를 다 설치하지 못한 경우, 좁혀야 함
    return False    
    
# 이분탐색
def binary_search():
    left = 1
    right = max(houses) - min(houses)

    while left <= right:
        n = (left + right) // 2
        
        result = can_build(n)
            
        # 설치 가능: 일단 설치하고, 더 넓힐 수 있나 확인
        if result:
            answer = result
            left = result + 1
            
        # 설치 부가능: 더 줄여야 함
        else:
            right = n - 1
            
    return answer

print(binary_search())

시간 복잡도

• 첫 집과 끝 집 간 거리를 $M$로 두고, 집의 수를 $N$으로 두었을 때
• 집의 좌표를 정렬할 때 $O(N \log N)$
• 이분 탐색이 최대 $O(\log M)$번 이루어짐
  • 각 이분 탐색에서 $O(N)$ 시간 복잡도의 can_build 함수 실행
• 더하면 $O(N \log M + N \log N)$인데
  • $N \leq M$이므로 $O(N \log M)$
• $N \leq 200,000$이며, $M <= 1,000,000,000$인데 $\log M$은 보통 무시할 정도로 작기 때문에, 2초 안에 풀 수 있음.

기억할 점

• 상록아, 발상을 역전시키는 거야!