백준 / 골드 2 / 2637. 장난감 조립

과자와 사탕을 싣고서~

생각해봅시다!

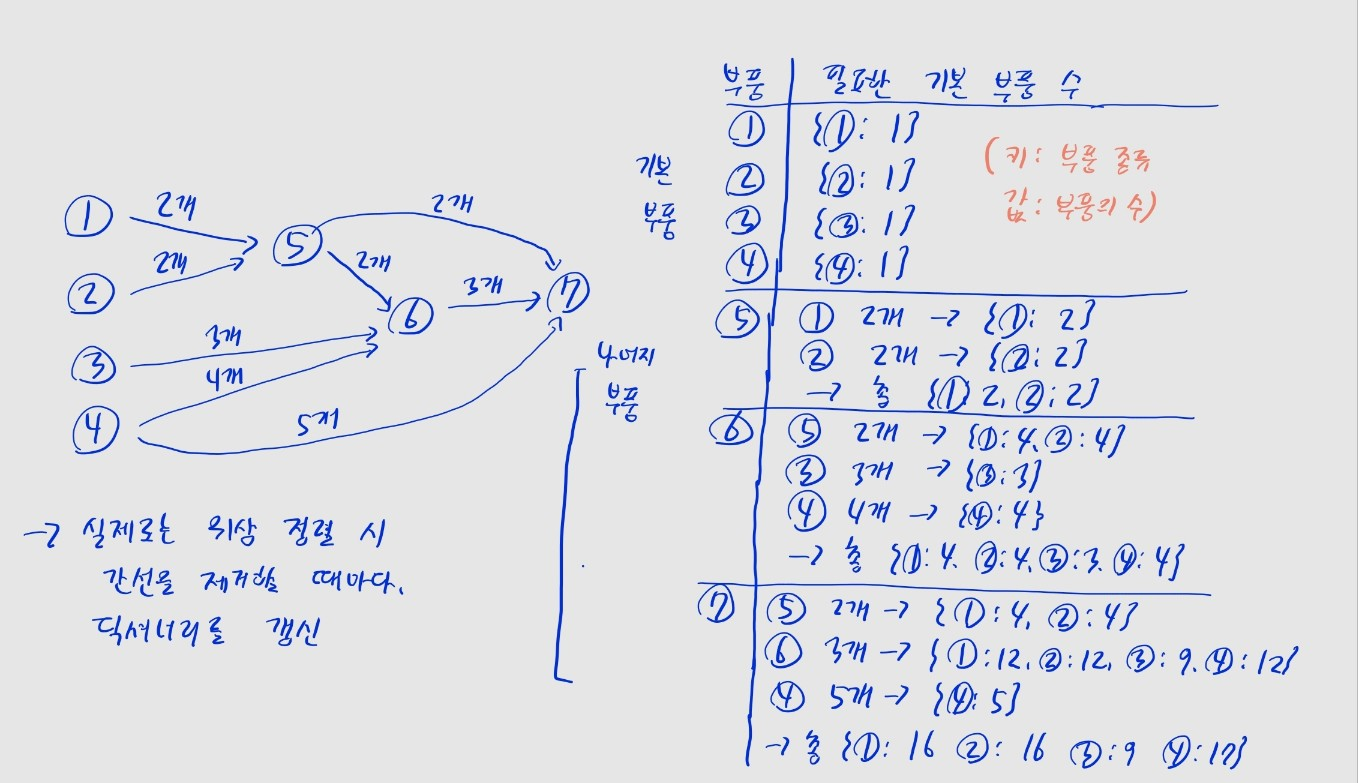
• 부품 5는 2개의 부품 1과 2개의 부품 2로 만들어진다?
• 부품 6은 2개의 부품 5와 3개의 부품 3으로 만들어진다?
  • 작업 간 순서가 정해져 있다는 점에서 위상 정렬 문제 같아 보이네요
• 근데 이 문제에서는 각 부품을 만들 때 몇 개의 기본 부품이 필요한지 저장해 두는 게 중요해요
  • 일단 제 풀이에선, 각 부품별로 딕셔너리를 만들어 줄 겁니다
  • 해당 부품을 만들 때 필요한 기본부품의 종류를 키로, 부품의 개수를 값으로 두어 관리하면 편리하겠죠?

입력 받기

from collections import deque, defaultdict
import sys
input = sys.stdin.readline

N = int(input())
M = int(input())
graph = [[] for _ in range(N + 1)]
indegree = [0] * (N + 1)
queue = deque()

for _ in range(M):
    a, b, k = map(int, input().split())
    # a를 만드는 데, b가 k개 필요함
    # b -> a로 향하는 간선
    graph[b].append((a, k))
    indegree[a] += 1

• 일단 위상 정렬을 할 거니까, 이에 맞게 그래프를 인접리스트 형태로 만들어줍니다
• 그래프의 b -> a 방향 간선은, a를 만들 때 b가 필요하다...라는 뜻입니다
• 이때 한 부품을 만들 때 다른 부품이 얼마나 필요한지 (k개) 역시 함께 저장합니다

딕셔너리 사용

# how_many의 i번째 인덱스: i번 부품을 만들 때 필요한 기본부품을 나타내는 딕셔너리
# 딕셔너리는 {기본부품1: a개, 기본부품2: b개} 형태
how_many = [defaultdict(int) for _ in range(N + 1)]

• 딕셔너리는 $N$개의 부품 각각에 대해 만들어 주고, how_many 리스트로 관리합니다
• how_many[i]는, i번 부품을 만들 때 각 기본부품이 몇 개 필요한지를 나타내는 딕셔너리입니다
  • 딕셔너리의 키는 기본부품의 종류, 값은 해당 기본부품의 종류가 됩니다
• 본 풀이에서는 defaultdict(int)를 사용합니다
  • 딕셔너리에 없는 키에 접근하는 경우, 자동으로 0의 값을 부여해 줘서 편합니다

위상정렬

# 맨 처음 진입차수가 0인 노드 (기본 부품)를 큐에 넣기
# 이때 기본 부품의 딕셔너리는 {자기 자신: 1개}
for i in range(1, N + 1):
    if indegree[i] == 0:
        queue.append(i)
        how_many[i][i] = 1

• 평소 위상정렬을 했던 것처럼, 진입차수가 0인 노드부터 큐에 넣습니다
• 진입차수가 0인 노드는 만들 때 다른 부품이 필요하지 않은, 기본 부품입니다
• 기본 부품은 다른 부품 없이 자기 자신만으로 구성되므로, {자기 자신: 1}의 형태로 초기화합니다.
  • e.g., 1번 부품의 딕셔너리 how_many[1]은, {1: 1}로 설정합니다

# 위상 정렬
while queue:
    x = queue.popleft()            
    for y, count in graph[x]:
    	# 노드 x에서 y로 향하는 간선을 없앨 때마다,
        indegree[y] -= 1
        
        # y를 만들 때 필요한 부품 수를 딕셔너리에 갱신
        for b in how_many[x]:
        	# (x를 만들 때 필요한 부품 수) * (필요한 부품 x의 수)
            how_many[y][b] += how_many[x][b] * count
        
        if indegree[y] == 0:
            queue.append(y)

• 이후 큐에서 노드를 꺼내고, 노드에서 나가는 간선을 제거하고, 들어오는 간선이 0이 된 노드를 큐에 삽입하는 과정을 반복합니다
• 이때 노드 x에서 y로 향하는 간선을 제거할 때...
  • 부품 y를 만들 때 count개의 부품 x가 필요하다고 합시다
  • 이를 반영해 부품 y의 딕셔너리를 갱신해 줍니다.
  • x의 딕셔너리에서 필요한 각 기본부품별 개수를 확인하고
  • 각 개수를 count로 곱해, y의 딕셔너리에 더해 주면 됩니다
• y의 딕셔너리에 키가 없어도 바로 더해 줘도 됩니다. 없는 키로 접근하면 0의 값을 반환하는 defaultdict 덕분임

for i in range(1, N + 1):
    result = how_many[N][i]
    if result != 0:
        print(i, result)

• 이 과정이 완료되면, 마지막 부품의 딕셔너리를 순회하면서 기본 부품이 각각 몇개 필요한지 출력합니다
• 기본부품의 번호만 키로 존재하는데, defaultdict는 없는 키에 접근하면 바로 0을 반환합니다
• 즉 result != 0인 경우만 출력하면 되겠죠

최종 풀이

from collections import deque, defaultdict
import sys
input = sys.stdin.readline

N = int(input())
M = int(input())
graph = [[] for _ in range(N + 1)]
indegree = [0] * (N + 1)
queue = deque()

for _ in range(M):
    x, y, k = map(int, input().split())
    # x를 만드는 데, y가 k개 필요함
    # y -> x로 향하는 간선
    graph[y].append((x, k))
    indegree[x] += 1
    
# how_many의 i번째 인덱스: i번 부품을 만들 때 필요한 기본부품을 나타내는 딕셔너리
# 딕셔너리는 {기본부품1: a개, 기본부품2: b개} 형태
how_many = [defaultdict(int) for _ in range(N + 1)]

# 맨 처음 진입차수가 0인 노드 (기본 부품)를 큐에 넣기
# 이때 기본 부품의 딕셔너리는 {자기 자신: 1개}
for i in range(1, N + 1):
    if indegree[i] == 0:
        queue.append(i)
        how_many[i][i] = 1
         
# 위상 정렬
while queue:
    x = queue.popleft()            
    for y, count in graph[x]:
    	# 노드 x에서 y로 향하는 간선을 없앨 때마다,
        indegree[y] -= 1
        
        # y를 만들 때 필요한 부품 수를 딕셔너리에 갱신
        for b in how_many[x]:
        	# (x를 만들 때 필요한 부품 수) * (필요한 부품 x의 수)
            how_many[y][b] += how_many[x][b] * count
        
        if indegree[y] == 0:
            queue.append(y)

for i in range(1, N + 1):
    result = how_many[N][i]
    if result != 0:
        print(i, result)

시간 복잡도

• 노드 수(부품 수)를 $N$, 간선 수(부품 간 관계 수)를 $M$으로 둘 때
• 일반적인 위상정렬의 시간 복잡도는 $O(N + M)$

# y를 만들 때 필요한 부품 수를 딕셔너리에 갱신
for b in how_many[x]:
	# (x를 만들 때 필요한 부품 수) * (필요한 부품 x의 수)
	how_many[y][b] += how_many[x][b] * count

• 단 본 코드에서는, 간선을 제거할 때마다 딕셔너리를 갱신
  • 기본 부품의 수를 $B$로 둘 때, 위 연산엔 $O(B)$ 소요
  • 간선이 총 $M$개이므로 $O(B \times M)$, 모든 부품이 기본 부품인 경우 $O(N \times M)$
• 따라서 $O(N \times M)$이지만.. $N \leq 100$, $M \leq 100$이므로 시간초과 걱정은 없음

기억할 점

• 딕셔너리 관리가 복잡한 문제가 있다...? defaultdict를 써라.