

쉽게 설명하기 빡세서 좀 코드랑 수식의 항연이에요. 미리 죄송합니다리미.
생각해봅시다!
- LCS는 꽤나 유명한 동적 계획법을 활용하는 문제입니다.
- 그런데 점화식을 떠올리는 게 썩 쉽진 않아요... 이걸 풀이 안 보고 혼자 풀었다면 천재 인정.
- 하지만 웬만한 알고리즘 책이나 강의에서 예제로 소개해 주는 문제인 만큼, 걍 풀이 보셔도 죄책감은 안 느껴도 될 듯 합니다.
LCS (최장 공통부분 수열)
- LCS는 두 수열에 공통으로 존재하는 부분 수열 중, 길이가 가장 긴 수열입니다.
- 부분 수열은 수열에서 순서를 유지한 채로, 일부 원소를 선택해 만든 수열입니다.
- e.g.,
ACAYKP와CAPCAK의 LCS는ACAK입니다.- ACAYKP, CAPCAK
LCS 함수 정의하기
- 결국에 우리의 목표는 두 문자열의 LCS의 길이를 구하는 거니까, 그 역할을 해 줄 함수가 필요합니다.
- 함수
LCS(i, j)를 정의합니다.- 두 문자열
A,B가 주어질 때,A[:i]와B[:j]의 LCS의 길이를 반환합니다. A[:i]가 문자열을0번째부터i-1번째 인덱스까지 슬라이싱한 결과라는 것을 기억합시다.
- 두 문자열
A의 길이를N,B의 길이를M으로 두면,i는0부터N,j는0부터M까지의 값을 가질 수 있습니다.
i == 0 or j == 0일 때
i == 0인 경우A[:i]는A[:0], 즉 아무 글자도 없는 빈 문자열이 됩니다.- 마찬가지로
j == 0인 경우B[:j]도 빈 문자열이 됩니다.
- 마찬가지로
- 빈 문자열 내 부분 수열의 최대 길이는
0이므로, 둘 중 하나라도 빈 문자열인 경우 LCS의 길이는0이 됩니다. - 결론:
i == 0orj == 0일 때,LCS(i, j) = 0
i >= 1 and j >= 1일 때
- 기존
A[:i-1]과B[:j-1]의 LCS(LCS(i - 1, j - 1))에 각각 새로운 문자A[i-1]과B[j-1]가 추가되어,A[:i]와B[:j]가 됐다고 생각합시다.- 이때 우리는 새로운 두 문자열의 LCS(
LCS(i, j))를 구해야 합니다.
- 이때 우리는 새로운 두 문자열의 LCS(
- 새로 추가된 문자인
A[i - 1]과B[j - 1]을 비교합니다.

- 새로 추가된 문자가 동일한 경우 (
A[i - 1] == B[j - 1])- 기존 LCS에 마지막 문자를 새로 포함시킬 수 있습니다.
- 기존 LCS의 길이인
LCS(i - 1, j - 1)에 1을 더해주면 됩니다. - 결론:
A[i - 1] == B[j - 1]인 경우,LCS(i, j) = LCS(i - 1, j - 1) + 1
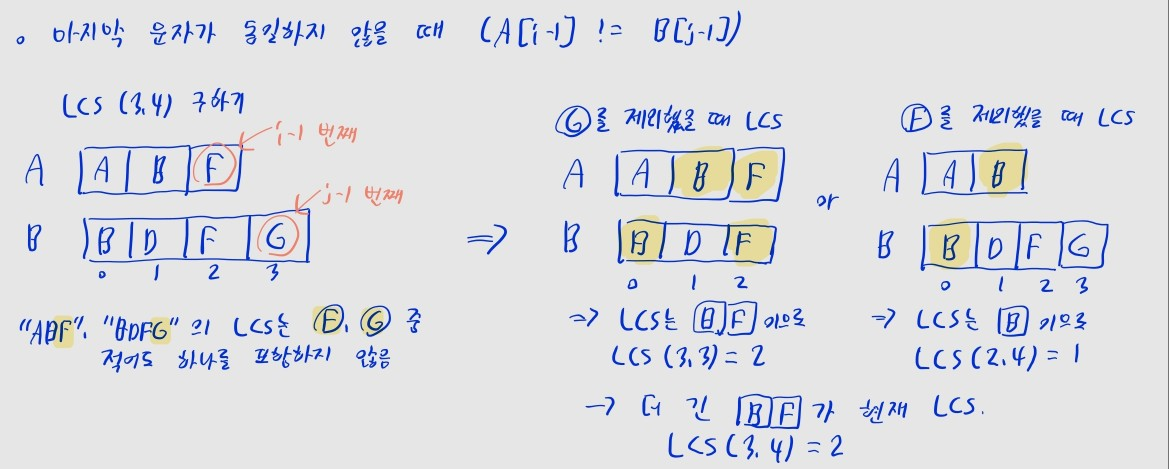
- 새로 추가된 문자가 동일하지 않은 경우 (
A[i - 1] != B[j - 1])- 기존 LCS에
A[i - 1]과B[j - 1]을 모두 포함할 순 없습니다. 즉, 한 쪽을 버려야 합니다. - 즉
A쪽에 추가된A[i - 1]을 제외했을 때, LCS의 길이인LCS(i - 1, j)와 B쪽에 추가된B[j - 1]을 제외했을 때, LCS의 길이인LCS(i, j - 1)중- 더 큰 값이 현재 LCS의 길이인
LCS(i, j)가 됩니다. - 결론:
A[i - 1] != B[j - 1]인 경우,LCS(i, j) = max(LCS(i - 1, j), LCS(i, j - 1))
- 기존 LCS에
정리
LCS(i, j) | 반환값 |
|---|---|
i == 0 or j == 0 | 0 |
i >= 1 and j >= 1A[i-1] == B[j-1] | LCS(i-1, j-1) |
i >= 1 and j >= 1A[i-1] != B[j-1] | max(LCS(i, j-1), LCS(i-1, j) |
- 이제 이대로 함수를 만드시면 됩니다!
풀이
# 재귀를 좀 많이 할 것 같으니 미리 제한을 풀어 놓읍시다
import sys
sys.setrecursionlimit(10 ** 9)
# 문자열 A 및 B
str_A = input()
str_B = input()
N = len(str_A)
M = len(str_B)
# memo[i][j]는 LCS(i, j)의 값을 저장
memo = [[None] * (M + 1) for _ in range(N + 1)]
# str_A[:i]과 str_B[:j]의 LCS 길이를 구함
def LCS(i, j):
if i == 0 or j == 0:
return 0
elif memo[i][j] is None:
# 마지막 문자가 동일하면
if str_A[i - 1] == str_B[j - 1]:
# 마지막 문자를 제외한 LCS의 길이에, 1을 더함
memo[i][j] = LCS(i - 1, j - 1) + 1
else: # 마지막 문자가 다르면
# 적어도 한쪽의 마지막 문자는 LCS에 존재하지 않으니
# 양쪽에서 제거한 결과를 비교하고, 더 긴 길이를 반환
result_a = LCS(i - 1, j)
result_b = LCS(i, j - 1)
memo[i][j] = max(result_a, result_b)
return memo[i][j]
# 두 (전체)문자열의 LCS 길이
print(LCS(N, M))시간 복잡도
- 두 문자열의 길이를 , 으로 돌 때
- 결국엔
LCS(0, 0)부터LCS(N, M)까지 값을 1번씩 구하므로- 연산량은
- 최종 . 이므로 번.
- Python 3 기준 시간제한은 2초인데, 그 안에 통과 가능!
재귀 없이 반복문으로도 풀 수 있음
- 보통 이런 걸 상향식 접근이라고도 부릅니다
- 이러면
LCS(i, j)함수는 필요없고, 반복문으로 바로 2차원memo리스트를 채우게 됩니다 - 사용하는 점화식은 동일함
i==0 or j==0인 경우0str_A[i - 1] == str_B[j - 1]인 경우,memo[i][j] = memo[i-1][j-1] + 1- 아닌 경우,
memo[i][j] = max(memo[i-1][j], memo[i][j-1])
str_A = input()
str_B = input()
N = len(str_A)
M = len(str_B)
# memo[i][j]는
# memo[:i]과 memo[:j]의 LCS 길이를 구함
memo = [[0] * (M + 1) for _ in range(N + 1)]
for i in range(1, N + 1):
for j in range(1, M + 1):
# 마지막 문자가 동일하면
if str_A[i - 1] == str_B[j - 1]:
# 마지막 문자를 제외한 LCS의 길이에 1을 더함
memo[i][j] = memo[i-1][j-1] + 1
# 마지막 문자가 동일하지 않으면
else:
# .... 이건 걍 글 설명 보쇼
memo[i][j] = max(memo[i-1][j], memo[i][j-1])
# 두 (전체)문자열의 LCS 길이
print(memo[N][M])

잠은 언제자니