자료구조 & 알고리즘 관련 개념 정리

개발자 강세영·2023년 6월 9일

공간복잡도 그리디 알고리즘 동적 프로그래밍 리틀 오 리틀 오메가 분할상환분석 분할정복 빅-오 시간복잡도 알고리즘 알고리즘 설계기법 자료구조 추상자료형

TIL

목록 보기

56/70

자료구조(Data Structure)

자료구조란 컴퓨터가 데이터를 효율적으로 다룰 수 있게 도와주는 데이터 보관 방법과 데이터에 관한 연산의 총체를 뜻한다.
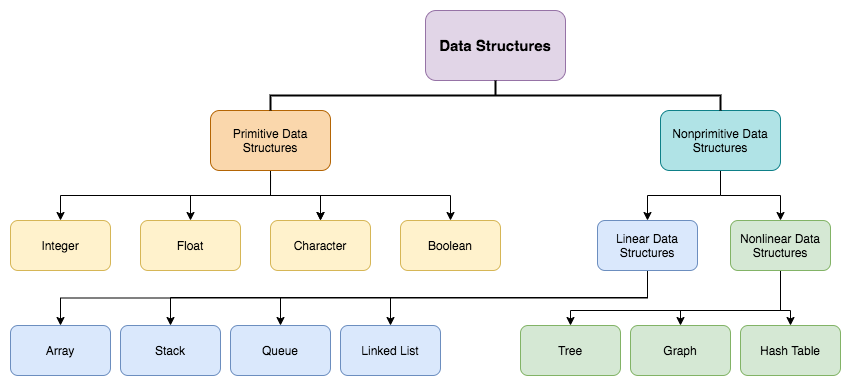
자료구조는 단순(primitive) 자료구조와 복합(non-primitive) 자료구조로 나뉜다.
단순 자료구조란 여러 프로그래밍 언어에서 기본적으로 지원하는 int, float, boolean 등의 자료형을 말한다. 원시 자료구조라고 부르기도 한다. 단순 자료구조는 대부분 더 이상 나눌 수 없는 원자적인 값들로 이루어져 있다.
자료형과 자료구조의 차이:
자료형이란 컴파일러 또는 인터프리터에게 프로그래머가 데이터를 어떻게 사용하는 지를 알려주는 일종의 데이터 속성(attribute)이다. 자료형은 자료구조에 비해 훨씬 더 구체적이며, 특정 언어의 자료형은 해당 언어의 원시적인 자료형(int, float, string 등) 뿐만 아니라 언어에서 지원하는 모든 자료형을 포함한다.
복합 자료구조란 단순 자료구조를 기반으로 만들어낸 배열, 스택, 트리 등과 같은 자료구조를 말한다. 복합 자료구조는 크게 선형(linear)과 비선형(non-linear)로 나뉜다.
선형 자료구조는 데이터 요소를 순차적으로 연결하는 자료구조 이며 데이터 간의 관계가 1:1 이다. 대표적인 종류는 다음과 같다.
- 배열(array)
- 연결 리스트(linked list)
- 스택(stack)
- 큐(queue)
비선형 자료구조는 데이터 요소를 비순차적으로 연결하며 데이터 간의 관계가 1:N 또는 N:M 등으로 복잡하게 연결되고 계층 구조를 갖는 자료구조이다. 대표적인 종류는 다음과 같다.
- 트리(tree)
- 그래프(graph)

추상 자료형(Abstract Data Types, ADT)

추상 자료형 또는 추상적 자료형이란 자료구조의 동작 방법을 표현하는 형식을 말한다. 이는 자료구조가 갖춰야 할 일련의 연산이라고 할 수 있다.
리스트의 예를 들면, 리스트는 데이터에 순차적으로 접근해서 그 데이터를 다룰 수 있는 기능을 제공해야 한다. 리스트의 특정 위치에 있는 노드에 접근(get)하거나, 리스트의 마지막에 데이터를 추가(append)하거나, 마지막에 있는 데이터를 삭제하거나(pop), 중간에 삽입(insert)하거나, 삭제(remove)하는 기능이 필요하다. 이러한 정의를 한 것이 추상 자료형이다.
그러나 추상 자료형은 전체적인 구조와 기능들에 대한 구체적인 구현 방법을 명시하지 않는다. 자료구조의 내부적인 구성이 어떻게 돼있는 지, 연산 작업은 어떻게 실행되는지, 연산에 대한 시간 복잡도 등 세부적인 사항을 다루지 않는다.
즉, 추상 자료형은 데이터의 구조와 동작에 대한 청사진을 제시하는 것이고 자료구조는 추상 자료형을 구체적으로 구현한 것이다.
리스트라는 추상 자료형을 구체적으로 구현한 자료구조가 바로 연결 리스트라고 볼 수 있다.
추상 자료형(ADT)과 대표적인 자료구조의 예시는 다음과 같다.

ADT	자료구조 예시
리스트	(단순, 이중, 원형 등)연결 리스트
스택	배열 기반 스택, 연결 리스트 기반 스택
큐	환형 큐, 링크드 큐
트리	이진 트리, LCRS 트리, 레드-블랙 트리
그래프	방향 그래프, 무방향 그래프
힙	배열 기반 힙, 연결 리스트 기반 힙

알고리즘(Algorithm)

알고리즘이란 페르시아의 수학자 알 콰리즈미(Al-Khwarizmi)의 이름에서 유래된 말로 어떤 문제를 풀기 위한 단계적 절차를 의미한다.
책장을 예로 들면, 내가 책을 찾아야 하는데 왼쪽부터 찾을 것인지, 오른쪽부터 찾을 것인지, 무작위로 찾을 것 인지를 결정하는 것이 알고리즘이다.
컴퓨터를 사용해서 주어진 문제를 해결하는 알고리즘은 다음과 같은 조건을 모두 만족해야 한다.
1. 입출력: 외부에서 0개 이상의 입력을 받아서 하나 이상의 출력을 생성해야 한다.
2. 명확성: 각 단계(명령)는 모호하지 않으며 단순하고 명확해야 한다.
3. 유한성: 한정된 수의 단계를 거친 후에는 반드시 끝나야 한다.
4. 유효성: 모든 명령은 컴퓨터에서 수행할 수 있어야 한다.
위의 조건들을 종합하면 알고리즘이란 주어진 문제에 대한 하나 이상의 결과를 생성하기 위해 모호하지 않고 단순 명확하며 컴퓨터가 수행할 수 있는 유한개의 일련의 명령어들을 순서에 따라 구성한 것이라고 할 수 있다.
현실 세계의 다양한 문제들을 해결하기 위한 다양한 알고리즘이 이미 존재하며, 자신만의 새로운 알고리즘을 만들 수도 있다.
알고리즘을 표현하는 방법으로는 일상적인 언어(자연어), 의사 코드(pseudo-code), 순서도(flow chart), 프로그래밍 언어(programming language) 등이 있다.
알고리즘의 효율성을 평가하는 척도로 시간 복잡도와 공간 복잡도가 있다.

시간 복잡도(time complexity), 공간 복잡도(space complexity), 점근 표기법(asymptotic notation)

시간 복잡도와 공간 복잡도 모두 넓게는 계산 복잡도(Computational Complexity)에 포함되는 개념이다. 계산 복잡도란 알고리즘을 수행하는데 필요한 자원(시간, 메모리 등)을 의미한다.
시간 복잡도란 알고리즘의 입력 값과 연산 수행 시간의 상관 관계를 나타내는 척도이다. 일반적으로 점근 표기법을 이용하여 나타낸다.
공간 복잡도란 알고리즘의 수행에 필요한 자원 공간(메모리)을 말한다. 일반적으로 주기억장치만 고려하며 시간 복잡도와 마찬가지로 점근 표기법으로 나타낸다.
알고리즘은 흔히 시간과 공간의 트레이드오프(space-time tradeoff) 관계가 된다. 즉, 실행 시간이 빠른 알고리즘은 공간을 많이 사용하고, 공간을 적게 차지하는 알고리즘은 실행 시간이 느리다는 것이다.
점근 표기법이란 알고리즘의 수행 시간을 대략적으로 나타내는 방법이다. 입력 크기가 커질 수록 최고차항이 수행 시간에 미치는 영향이 매우 크며, 최고차항 외에 다른 항과 계수의 효과는 무시해도 될 정도로 점점 작아진다. 따라서 점근 표기법은 최고차항만 표기하고 계수는 무시한다.
입력 값 $n$ 에 대해 $3n^2+2n+1$ 번 만큼 계산하는 함수가 있다면 이 함수의 최고차항인 $3n^2$ 에서 계수를 제거한 $n^2$ 만을 시간 복잡도로 나타낸다.
점근 표기법으로는 알고리즘의 정확한 수행시간을 나타낼 수 없지만 입력 크기에 따른 수행시간의 증가 추세를 쉽게 파악할 수 있기 때문에 알고리즘의 성능을 분석하고 비교할 때 매우 유용하다.

Big O, Big Omega, Big Theta

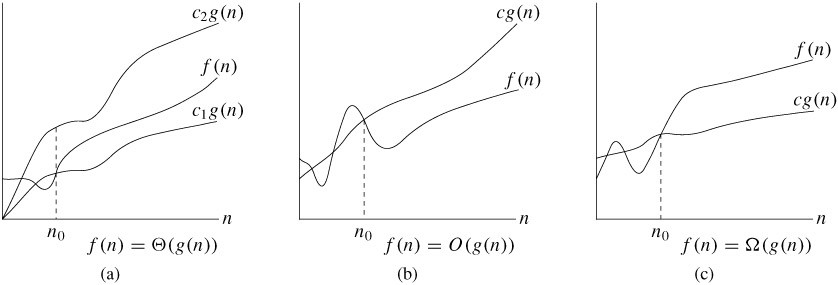
대표적으로 사용되는 시간 복잡도의 점근 표기법으로 O(Big O, Big Oh, Big Omicron, 빅 오), Ω(Big Omega, 빅 오메가), Θ(Big Theta, 빅 세타) 가 있다.
빅 오(O) 표기는 알고리즘 수행 시간의 상한(upper bound)이다. 위 그림의 $f(n)$ 과 같은 어떤 복잡한 함수의 실행 시간이 주어질 때, 가장 늦게 실행된다면 이만큼 걸린다는 의미이다.
빅 오메가(Ω) 표기는 알고리즘 수행 시간의 하한(lower bound)이다. 위 그림의 $f(n)$ 이 가장 빨리 실행된다면 이만큼 걸린다는 의미이다.
빅 세타(Θ) 표기는 평균적인(tight bound) 알고리즘 수행 시간을 나타낸다. 집합으로 표현하면 빅 오 표기법과 빅 오메가 표기법의 교집합이라 할 수 있다.
위의 표기법은 시간 복잡도 표기법 of ~ 라고 읽는다. 예를 들어 $O(1)$ 는 big O of 1이라고 읽으면 된다.
빅 오가 최악의 경우의 실제 수행시간을 나타낸다고 오해하기 쉬우나 이는 잘못된 것이다. 빅 오는 수행 시간의 상한을 의미할 뿐 최악의 경우에는 항상 빅 오 만큼 시간이 걸린다는 의미는 아니다. 함수의 실제 수행시간과 점근 표기법은 별개로 생각해야 한다.
예를 들어 최악의 경우 시간 복잡도가 $O(n^2)$ 이다 라는 말은 최악의 경우에는 필요한 연산량이 $n^2$ 이내라는 의미이다. 빅 오는 수행시간의 상한이므로 실제 수행시간이 이보다 작기만 하면 되기 때문에 최악의 경우 시간 복잡도가 $O(n^3)$ 라는 명제또한 참이 된다. 하지만 실제 수행시간과 $O(n^2)$ 의 오차보다 $O(n^3)$ 의 오차가 더 크므로 이러한 명제는 별 의미가 없다.
알고리즘의 수행 시간이 최선인 상황은 드물고, 평균적인 상황은 알아내기 어렵기 때문에 대개 알고리즘의 시간 복잡도는 빅 오 표기법으로 나타낸다. 코딩 문제 또한 시간이나 메모리 제한이 있기 때문에 이를 만족하는 빅 오를 고려하며 푸는 것이 좋다.
입력 크기가 충분히 커야(위 그래프에서 $n_0$ 로 표시된 것) 점근 표기법대로 나오는 것을 확인할 수 있다. 예를 들어 1GB 정도 크기의 파일을 100Mbps 정도의 속도로 전송한다면 그냥 인터넷으로 보내면 되지만 페타바이트나 엑사바이트 급의 아주 큰 용량을 전송해야 한다면 파일이 담긴 디스크를 비행기로 수송하는 것이 더 효율적이다. 온라인 전송의 시간 복잡도는 파일의 크기에 비례하므로 $O(n)$ 이지만 비행기로 디스크를 수송하는 것의 시간 복잡도는 파일의 크기와 상관없이 거의 일정하므로 $O(1)$ 이기 때문이다.
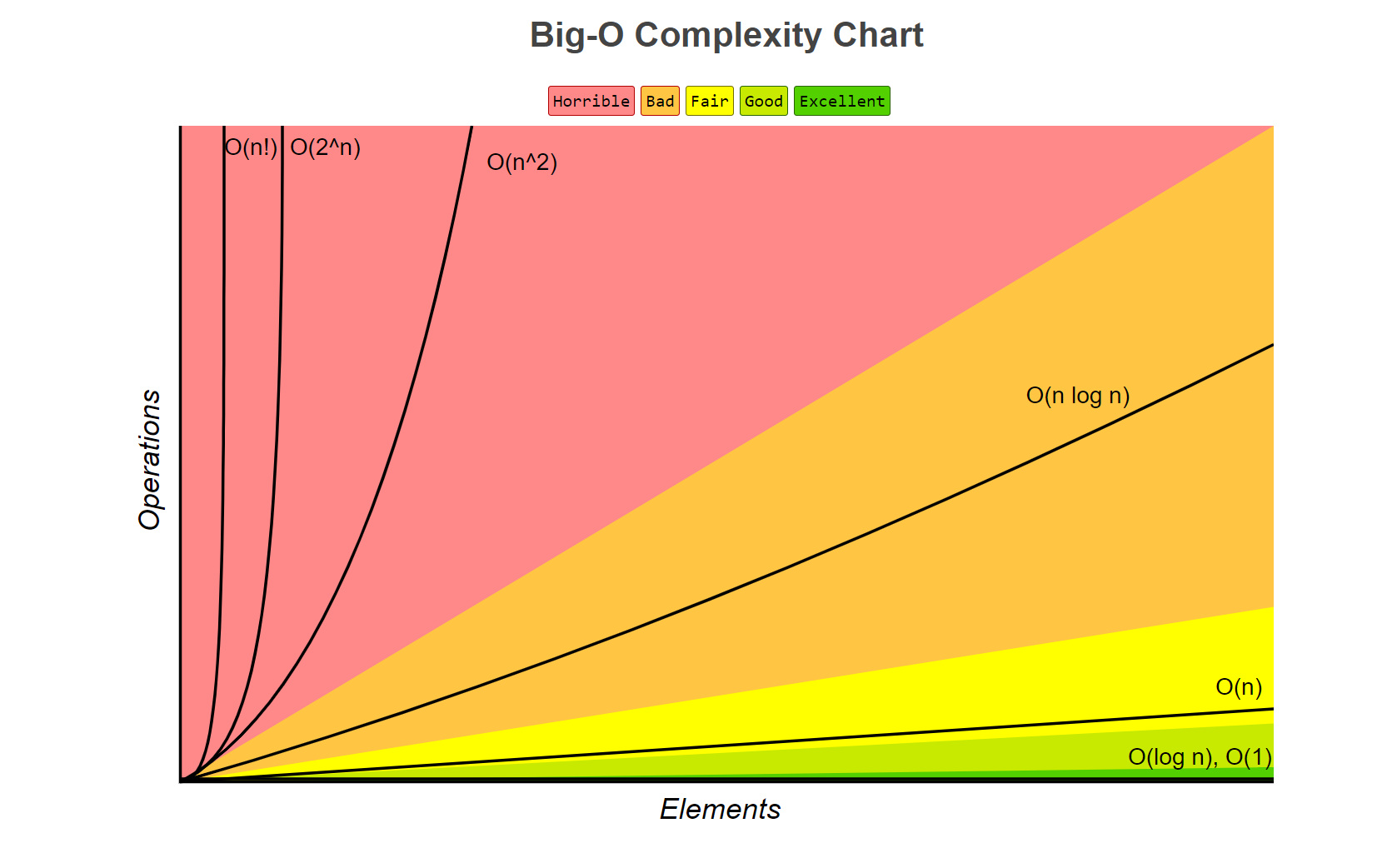
점근 표기법으로 나타낸 알고리즘의 시간 복잡도는 몇 가지의 패턴을 갖는데, 효율적인 순서로 정리하면 다음과 같다.
이 순서는 점근 표기법의 종류에 상관없이 공통적으로 적용된다.
- $O(1)$ : 입력 크기가 아무리 커도 실행 시간은 일정하여 상수 시간(constant time)이라고 부르며 가장 효율적인 알고리즘이다. 배열의 인덱스로 데이터에 접근하거나 해시 테이블을 이용한 데이터 접근(충돌이 없을 때)이 이에 해당한다.
- $O(log n)$ : 여기서부터 실행 시간이 입력 크기에 비례하여 증가한다. 이 복잡도는 로그 함수에 비례하기 때문에 로그 시간(logarithmic time)이라고 부른다. 로그 함수의 기울기는 매우 완만하기 때문에 일반적으로 좋은 알고리즘이다. 대표적인 예로 이진 탐색이 있다. 로그의 밑은 보통 2이다.
- $O(n)$ : 알고리즘의 수행 시간이 입력 크기에 선형적으로 비례하여 선형 시간(linear time)이라고 부른다. 대표적인 예로 선형 탐색이 있다.
- $O(n log n)$ : 선형 시간과 로그 시간의 곱으로 $O(n)$ 과 $O(log n)$ 보다 기울기가 훨씬 가파르다. 이 복잡도는 선형 로그 시간(linearithmic time)이라고 부르며 비교(comparison) 정렬 알고리즘의 성능 한계이다. 비교 정렬 중 병합 정렬 같은 효율 좋은 정렬 알고리즘이 이에 해당한다. 로그의 밑은 보통 2이다.
- $O(n^2)$ : 입력 크기 n에 대해 제곱으로 수행 시간이 늘어난다. 여기서부터는 기울기가 매우 가파르기 때문에 느린 알고리즘으로 평가한다. 버블 정렬, 삽입 정렬 등 비효율적인 정렬 알고리즘이 이에 해당한다.
- $O(n^3)$ : 입력 크기 n에 대해 세 제곱으로 수행 시간이 늘어난다. 행렬 곱셈이 이에 해당한다.
- $O(2^n)$ : 입력 크기 n에 대해 2의 n제곱만큼 수행 시간이 늘어난다. n이 조금만 커져도 $O(n^3)$ 보다 수행 시간이 느려진다. 피보나치 수를 재귀로 계산하는 알고리즘이 이에 해당한다.
- $O(n!)$ : 팩토리얼 시간이라고 부르며 입력 값이 조금만 커져도 웬만한 다항 시간 내에는 계산이 어렵다. 외판원 문제를 브루트 포스 탐색으로 해결하는 것이 이에 해당한다.
- $O(n!)$ 보다 느린 시간 복잡도로는 지수 시간(exponential time, $2^{{\text{poly}}(n)}$ )과 이중 지수 시간(double exponential time, $2^{2^{{\text{poly}}(n)}}$ )등이 있다.

little o(small o), little omega(small omega)

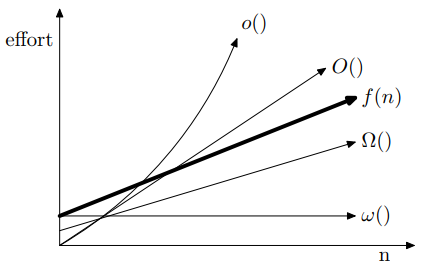
리틀 오와 리틀 오메가는 시간 복잡도를 보다 정확하게 나타내기 위해 사용하는 표기법이다. 이 표기법은 자주 사용되지는 않지만 논문 등의 엄밀한 표현이 필요한 문헌에서 가끔 볼 수 있다.
리틀 오(소문자 o-로 표기)는 함수의 증가율이 점근적 의미에서 어느 한계보다 더 작다는 것을 표현하고자 할 때 사용한다. 즉, 함수의 기울기상 여유있는 상한을 나타낸다.
리틀 오로 표기한 $o(g(n))$ 은 충분히 큰 n에 대해 $g(n)$ 에 아무리 작은 상수를 곱해도 $g(n)$ 이 압도하는 모든 함수의 집합이다. 예를 들어 $3n^2$ 은 $o(n^2)$ 에 속하지 않지만 $10n$ 은 충분히 큰 $n$ 에 대해서는 $o(n^2)$ 에 속한다.
빅 오와 리틀 오 비교:
$f(n) = 2n + 3$ 일 때
${f(n) = O(n)}$ 이지만, ${f(n) \ne o(n)}$ 이다.
$f(n) = O(n^2)$ 이고, $f(n) = o(n^2)$ 이다.
$f(n) = O(n^3)$ 이고, $f(n) = o(n^3)$ 이다.
$f(n) = a_xn^x + a_{x-1}n^{x-1} + ... + a_0$ 일 때
${f(n) = O(n^x)}$ 이지만, ${f(n) \ne o(n^x)}$ 이다.
$f(n) = O(n^{x+1})$ 이고, $f(n) = o(n^{x+1})$ 이다.
$f(n) = O(n^{x+2})$ 이고, $f(n) = o(n^{x+2})$ 이다.
리틀 오메가(오메가의 소문자 ω-로 표기)는 리틀 오와 정확히 대조되는 표기이다.
ω-표기는 함수의 증가율이 점근적 의미에서 어느 한계보다 더 크다는 것을 표현하고자 할 때 사용한다. 즉, 함수의 기울기상 여유있는 하한을 나타낸다.
예를 들면 $3n^2$ 는 $n^2$ 을 압도할 수 없으므로 $ω(n^2)$ 에 속하지 않는다.
$n^3$ 는 $n$ 이 1보다 크기만 하면 $n^2$ 를 압도하므로 $n^3=ω(n^2)$ 이다.

분할 상환 분석(Amortized Analysis, 상각 분석)

분할 상환 분석은 빅 오 표기법같이 함수의 동작을 설명하는 분석 방법이다. 분할 상환 분석에 의한 시간 복잡도나 공간 복잡도 또한 점근 표기법으로 나타낼 수 있다.
시간 복잡도와 공간 복잡도를 계산할 때 알고리즘 전체를 보지 않고 최악의 경우 만을 살펴보는 것은 지나치게 비관적이라고 하여, 이에 대한 대안으로 분할 상환 분석이 제시됐다.
분할 상환 분석은 알고리즘의 여러 연산이 서로 다른 실행 시간을 가지지만, 전체적으로 평균 실행 시간이 일정하게 유지되는 지를 분석하며 주로 다음과 같은 단계로 진행된다.
1. 계산을 실제로 수행하면서 발생하는 비용을 추적한다.
2. 여러 연산의 비용을 분할한다. 일부 연산은 실제 비용보다 더 많이 소모하는 경우가 있지만, 나머지 연산은 실제 비용보다 적게 소모한다.
3. 전체 연산에 대한 평균 비용을 계산하고, 각 연산의 평균 비용을 파악한다.
4. 연산의 평균 비용이 상한과 일치하는지, 즉 분할 상환 비용이 고르게 분배되는 지 확인한다.

병렬화

GPGPU를 이용한 병렬 연산으로 알고리즘의 실행 속도를 개선할 수도 있다.
병렬 연산이 가능한 하드웨어와 병렬 알고리즘의 성능이 빠르게 발전하면서 알고리즘 자체의 시간 복잡도 외에도 알고리즘의 병렬화 가능성 또한 알고리즘의 성능 평가에 있어서 중요한 척도가 되고 있다.

알고리즘 설계 기법

알고리즘의 설계는 주어지는 문제의 내용에 따라 매우 다양해질 수 있으므로 모든 문제에 대해서 일괄적으로 적용할 수 있는 알고리즘 설계기법은 존재하지 않는다.
하지만 비교적 간단하면서 많은 부류의 문제에 대해 적용할 수 있는 설계기법으로 그리디 알고리즘, 분할정복, 동적 프로그래밍 등이 있다.

그리디(Greedy) 알고리즘

그리디 알고리즘은 일련의 선택 과정을 통해 해를 찾는 방식으로, 각 선택의 시점에서 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방법이다. 탐욕법 또는 욕심쟁이 방법이라고도 부른다.
매 순간에 최적이라고 생각되는 해를 최적해를 국부적인(local) 최적해라고 한다. 그리디 알고리즘은 선택의 단계마다 국부적인 최적해를 선택하면 결과적으로 전체적인(global) 최적해를 구할 수 있다는 희망적인 전략을 취하는 방법이다.
그리디 알고리즘은 매우 간단하고 직관적이며, 일반적으로 다른 기법보다 효율적이라는 장점이 있다.
하지만 그리디 알고리즘으로 최적해를 구할 수 있는 문제는 제한적이며, 항상 전체적인 최적해를 구할 수는 없기 때문에 희망적인 전략을 취한다고 표현한다.
그리디 알고리즘의 대표적인 예시로는 거스름돈 문제, 배낭 문제 등이 있으며 크루스칼 알고리즘, 프림 알고리즘, 데이크스트라 알고리즘, 허프만 코딩 등이 이 기법을 활용하는 알고리즘이다.

거스름돈 문제(Change-making problem)

거스름돈 문제는 가능한 적은 수의 지폐나 동전을 사용하여 거스름돈을 주는 방법을 찾는 문제이다.
예를 들어 거스름돈이 540원이고 동전으로만 거슬러 주며 동전의 종류가 500원, 100원, 50원, 10원이라고 하자.
이 경우엔 먼저 가장 액면가가 높은 500원 동전 1개를 거스름돈에서 차감하여 잔액 40원을 구한다. 40원은 10원 동전 4개이므로 500원 동전 1개, 10원 동전 4개를 사용하여 총 5개의 동전으로 거스름돈을 주는 것이 최적이다.
이렇듯 액면가가 큰 것부터 거슬러주는 것이 국부적인 최적해이며, 이런 식으로 남은 거스름돈이 0원이 될 때까지 반복하면 가장 적은 수의 동전을 사용할 수 있다.
하지만 지폐나 동전의 액면가에 따라 최적해가 달라질 수 있으므로 그리디 알고리즘이 항상 최적해를 보장할 수는 없다.
위와 같이 동전 중 두개를 골랐을 때 두 동전의 최대공약수가 항상 낮은 동전으로 나오는 경우(500원과 100원의 최대공약수는 100원, 100원과 50원의 최대공약수는 50원, ...) 그리디 방식으로 문제를 풀 수 있지만, 그렇지 않은 경우 그리디 방식으로는 해결할 수 없다.
예를 들어 거스름돈이 650원이고 동전의 종류가 500원, 120원, 100원, 50원, 10원이면 그리디 알고리즘에 의한 최적해는 500원 1개, 120원 1개, 10원 3개로 총 5개의 동전을 사용하는 것이지만, 실제 최적해는 500원 1개, 100원 1개, 50원 1개로 총 3개의 동전을 사용하는 것이다.

배낭 문제(Knapsack problem)

배낭 문제는 어떤 배낭에 담을 수 있는 최대 용량이 주어져 있고, 각 물건은 무게와 가치를 가지고 있을 때, 배낭에 담은 물건들의 가치가 최대값이 되는 조합을 찾는 문제이다.
배낭 문제는 물건을 나누어 담을 수 있는 경우와 없는 경우가 있는데, 나누어 담을 수 있다면 물건의 단위 무게 당 가치를 구해서 배낭이 가득 찰 때까지 이 값이 높은 순서대로 물건을 담아나가는 그리디 방식으로 해결할 수 있다.
물건을 나눌 수 없는 경우의 배낭 문제는 0-1 배낭 문제라고 하며 이 문제는 그리디 알고리즘으로는 해결하기 어렵기 때문에 동적 계획법이나 백트래킹 등의 다른 설계기법으로 해결해야 한다.
예를 들어 배낭의 용량이 10이고 각 물건의 무게와 가치가 다음과 같을 때 0-1 배낭 문제로 가정하고 풀어보면 다음과 같다.
- 물건 1: 무게 3, 가치 15, 단위 무게 당 가치 5
- 물건 2: 무게 5, 가치 20, 단위 무게 당 가치 4
- 물건 3: 무게 3, 가치 9, 단위 무게 당 가치 3
- 물건 4: 무게 4, 가치 14, 단위 무게 당 가치 3.5
- 그리디 알고리즘에 의한 최적해는 물건 1, 2를 담는 것으로 총 가치는 35이다. 물건 2를 담은 다음에 배낭의 용량이 2 남아 있으므로 다음에는 4를 담아야 하지만 물건을 나눌 수 없으므로 배낭의 용량을 전부 채우지 못했다.
- 하지만 실제 최적해는 물건 1, 3, 4를 담는 것이며 총 가치는 38이다. 이처럼 0-1 배낭 문제의 경우 그리디 방식으로 해결하지 못한다는 것을 알 수 있다.

분할정복(Divide and Conquer)

분할정복은 순환적으로 문제를 해결하는 하향식 접근 방법이다. 주어진 문제의 입력을 더 이상 나눌 수 없을 때까지 나누어서 각각의 작은 문제를 해결한 후, 이 해를 결합하여 원래 문제의 해를 구하는 방법이다.
분할정복은 다음과 같은 세 단계의 작업으로 수행된다.
1. 분할(Divide): 주어진 문제의 입력을 여러 개의 작은 문제로 나눈다.
2. 정복(Conquer): 각각의 작은 문제를 순환적으로 분할한다. 문제가 더 이상 나눌 수 없을 정도로 충분히 작아지면 이 문제에 대한 해를 구한다.
3. 결합(Combine): 작은 문제의 해를 결합하여 원래 문제의 해를 구한다.
분할정복에서는 문제를 작게 쪼개는 작업이 중요하다. 작게 분할된 문제들은 원래 문제에 비해 크기만 작아졌을 뿐 해결방법은 원래 문제와 같고, 서로 독립적이기 때문에 각각의 작은 문제들에 대한 해를 순서에 맞게 합치면 원래 문제의 해를 구할 수 있다.
분할정복은 주로 재귀적(순환적, 자기호출)으로 구현되지만 문제에 따라 반복문으로 구현할 수도 있다. 분할정복의 대표적인 예시는 퀵 정렬, 병합 정렬, 이진 탐색 등이 있다.

동적 프로그래밍(Dynamic Programming, DP)

동적 프로그래밍 또는 동적 계획법은 크기가 가장 작은 부분 문제부터 해를 구해서 저장해 놓고, 이를 이용해서 더 큰 문제의 해를 점진적으로 만들어 가는 상향식 접근 방법이다.
DP라는 이름은 설계기법의 의미를 잘 반영하지 못하기 때문에 본질적인 의미를 살려서 기억하며 풀기라고 설명하기도 한다.
분할정복과 다르게 DP에선 작은 문제들이 서로 독립적일 필요가 없다. 따라서 초기 문제들의 해를 저장해두고 이를 다음 문제의 해를 구하는 데 활용할 수 있다.
동적 프로그래밍 방법은 주로 최적성의 원리(principle of optimality)가 성립하는 최적화 문제에 주로 사용된다. 최적성의 원리란 주어진 문제에 대한 최적해는 주어진 문제의 소문제에 대한 최적해로 구성된다는 원리이다.
즉, 동적 프로그래밍 방법을 적용하기에 앞서 문제에서 최적성의 원리가 성립하는지 먼저 증명하는 단계가 필요하다. 만약 어떤 문제가 최적성의 원리를 만족하면, 그 문제에 대한 최적해를 소문제에 대한 최적해의 형식으로 나타낼 수 있는 점화식을 만들 수 있다.
동적 프로그래밍 방법의 전체적인 처리 과정은 다음과 같다.
1. 주어진 문제에 대해 최적해를 제공하는 점화식을 도출한다.
2. 가장 작은 소문제부터 점화식의 해를 구한 뒤 이를 테이블에 저장한다.
3. 테이블에 저장된 소문제의 해를 이용하여 점차적으로 큰 상위 문제의 해를 구한다.
동적 프로그래밍의 대표적인 예시는 팩토리얼 연산, 피보나치 수열, 플로이드 알고리즘, 하노이의 탑, 연쇄 행렬 곱셈(Matrix chain multiplication), 최장 공통 부분 수열(Longest Common Subsequence) 등이 있다.
동적 프로그래밍의 핵심은 동일한 계산을 반복해야 할 경우 한 번 계산한 결과를 메모리에 저장해 두고 재사용하는 방식으로 중복 계산을 방지하는 것이다. 이를 메모이제이션(Memoization)이라고 하며 캐싱(caching)과 비슷한 개념이다.
메모이제이션과 비슷하지만 값을 미리 계산하는 기법을 타뷸레이션(Tabulation)이라고 한다.
메모이제이션은 값이 필요할 때 연산이 이루어지는 느긋한 연산(lazy evaluation)이고, 타뷸레이션은 필요하지 않은 값도 미리 연산을 해놓는 즉시 연산(eager evaluation)이라 할 수 있다.
두 기법을 비교하면 타뷸레이션의 초기화 오버헤드가 더 크지만, 일반적으로 시간 복잡도는 메모이제이션보다 타뷸레이션이 더 우수하다.
반드시 동적 프로그래밍으로 풀어야 하는 문제가 아닌 경우에도 시간이나 메모리의 제한으로 인해 메모이제이션이나 타뷸레이션 같은 동적 프로그래밍 기법이 필요할 때가 있다.