그래프(Graph)의 의미와 관련 용어 정리
- 컴퓨터 과학에서 그래프(Graph)란 이산수학의 한 분야인 그래프 이론의 무방향(undirected) 그래프와 방향(directed) 그래프 개념을 구현하기 위한 추상적 자료형이다.
- 그래프는 정점의 모음과 정점을 잇는 간선의 모음이 결합한 것이며 수학적으로 명확하게 표현하면 다음과 같다.
정점의 집합을 V, 간선의 집합을 E, 그래프를 G라고 했을 때 G=(V,E) 이다.
- 정점(vertex, 꼭지점) 또는 노드(node)는 그래프를 형성하는 기본 단위이다.
- 간선(edge, link, line) 또는 변은 정점들을 서로 연결하는 선이다. 그래프의 간선은 방향이 있을 수도 있고 없을 수도 있으며, 방향이 있다면 단방향과 양방향 모두 가능하다.
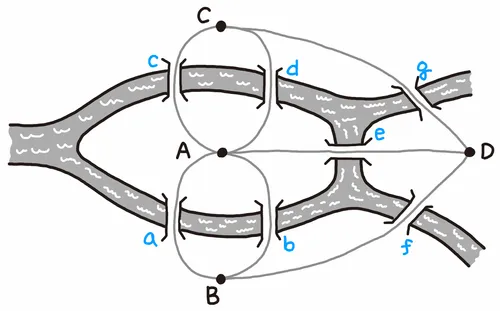
- 정점의 집합만 있는 경우 큰 의미가 없지만 이들이 간선을 통해 서로 연결되면 관계가 형성되고 이로 인해 그래프가 만들어진다. 그래프를 통해 현실 세계의 객체들의 관계를 모델링하여 나타낼 수 있고, 여러 가지 문제를 해결 하는데 활용할 수도 있다. 위의 그림은 쾨니히스베르크의 다리 건너기 문제를 그래프로 표현한 것이다.
- 그래프의 모든 간선이 방향을 가지고 있으면 방향(directed) 그래프, 방향을 가지지 않으면 무방향(undirected) 그래프, 방향이 있는 것도 있고 없는 것도 있으면 혼합(mixed) 그래프라고 한다.
- 정점간의 연결에 순서나 방향성이 존재하는 경우 방향 그래프가 유용하며, 이러한 관계가 없는 경우 무방향 그래프가 유용하다.
- 두 정점 사이에 한 개 이상의 간선을 허용하는 그래프는 다중 그래프라고 하며 두 정점 사이에 0개 또는 1개의 간선을 갖는 그래프는 단순 그래프라고 한다.
- 간선이 가중치(weight)를 갖는 그래프는 가중 그래프라고 한다. 간선의 가중치를 통해 지도 상의 두 지점 간의 거리나 비용 등을 나타낼 수 있다.
- 다른 어떤 정점과도 인접하지 않은 정점을 독립(고립, isolated) 정점이라고 한다. 독립 정점만으로 구성된 그래프는 널(NULL) 그래프라고 한다.
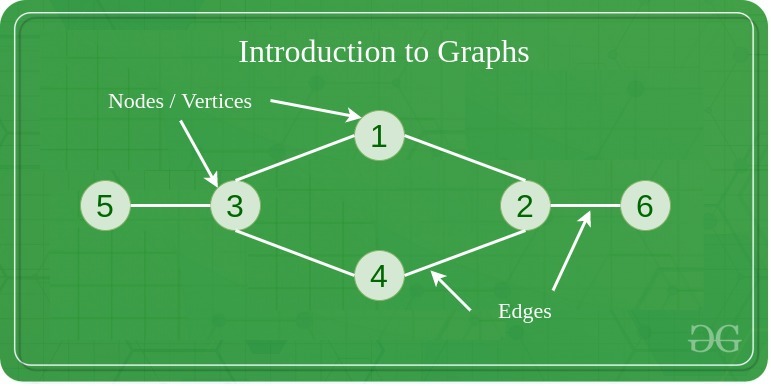
- 간선으로 연결된 두 정점을 가리켜 서로 인접(adjacent) 또는 이웃 관계에 있다고 말한다.
위 그래프에선 (5, 3), (3, 1), (1, 2), (2, 6), (2, 4), (3, 4)가 서로 인접 관계이다.
- 정점 v와 w가 서로 간선 e에 의해 연결된 상태라면 v와 w는 e에 의해 발생(incident)되었다고 한다.
- 그래프 G=(V,E)에 연결된 정점 v0와 vk가 있을 때, v0에서 vk까지의 워크(walk)란 다음과 같은 형태를 가지는 유한한 순서쌍이다. W=v0e1v1e2v2...ekvk
즉, 워크는 특정 경로 상의 정점과 변들을 순서대로 나열한 것이다.
- 워크 W에서 v0은 시작점, vk는 종점이라 하고 중간의 정점들은 내부점이라 한다. 시작점과 종점이 같을 경우 워크가 닫혀있다(closed)고 한다. k는 워크의 길이(length)라고 한다. 즉, 워크의 길이는 워크에 포함된 간선의 개수가 된다.
- 단순 그래프에선 워크에서 간선 부분을 생략하여 나타낼 수도 있다.
- 워크의 변들이 중복없이 모두 다르면 W는 트레일(trail)이라 하고, 정점이 모두 다르면 경로(path)라고 한다. 트레일이나 경로의 길이도 워크의 길이와 마찬가지로 간선의 개수로 구한다.
위 그래프에서 경로 (5-3-1)의 간선의 개수는 2이므로 길이는 2가 된다.
- 경로 상의 모든 정점이 서로 다르면 단순 경로(simple path)라고 하고, 경로 상의 모든 간선이 서로 다르면 기본 경로라고 한다.
- 트레일의 변이 모두 서로 다르면서 시작점과 종점이 동일한 경우 닫힌 트레일이라 한다.
- 닫힌 트레일에서 어떤 정점 하나를 두 번 이상 지나가면 사이클(cycle)이라고 한다. 위 그래프에서 경로 (3-1-2-4-3)은 사이클이다.
- 무방향 그래프에서 정점의 차수(degree)는 그 정점에 연결된 간선의 개수를 말한다.
- 그래프의 총 차수는 그래프에 있는 모든 정점에 대한 차수들의 합이다.
- 방향 그래프에서 진입 차수는 주어진 정점으로 향한 간선의 개수이며, 진출 차수는 주어진 정점에서 시작하는 간선의 개수이다. 정점의 차수는 진출 차수와 진입 차수의 합이다. 간선이 루프이면 차수에 2(진출 1 + 진입 1)를 더한다.
- 간선의 시작점과 끝점이 같은 정점의 길이가 1인 경로는 루프(loop)라고 한다.
- 두 정점을 연결하는 변이 두 개 이상 있을 때 이러한 변들을 병렬(parrallel) 변이라고 한다.
- 즉, 단순 그래프는 루프와 병렬 변이 없는 무방향 그래프를 의미한다.
- 그래프 G의 정점과 간선의 부분집합으로 구성된 그래프를 G의 부분 그래프(subgraph)라고 한다. 만약 이 부분 그래프의 정점과 원래 G의 정점이 완전히 일치하면 이 부분 그래프는 신장 부분 그래프(spanning subgraph)라고 한다.
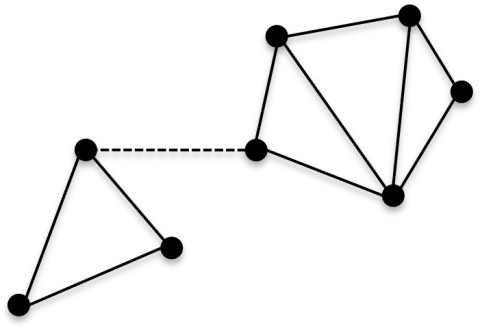
- 그래프 내의 두 정점 사이에 경로가 존재하면 이 두 정점이 연결되었다(connected)고 한다. 그래프에서 서로 연결된 정점들의 하위집합(부분 그래프)을 연결성분(connected component)이라고 한다. 그래프의 모든 정점이 연결된 상태라면 연결 그래프(connected graph)라고 한다. 즉, 연결 그래프는 오직 하나의 연결성분만 갖는 그래프이다.
- 위 그래프의 점선 부분이 간선이 되면 연결 그래프가 되지만 간선이 끊기면 연결되지 않은(disconnected) 그래프가 된다.
- 방향 그래프의 경우 서로 다른 두 정점 u, v의 모든 쌍에 대해서 u에서 v까지의 방향 경로와 v에서 u로의 방향 경로가 존재하면 그 방향 그래프는 강력하게 연결되었다(strongly connected)고 하고, 그렇지 않으면 약하게 연결되었다(weakly connected)라고 한다.
- 방향 그래프에서 강력하게 연결된 정점들을 강연결 성분(strongly connected component)이라고 한다. 즉 강연결 성분은 방향 그래프에서 임의의 두 정점 사이에 양방향의 경로가 존재하는 최대 부분 그래프이다.
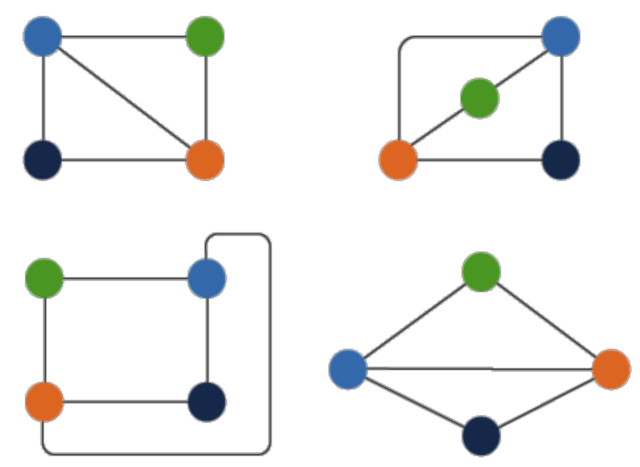
- 정점과 변의 이름을 제외하고 모두 동일한 그래프를 동형(isomorphic)이라 한다. 위 그림과 같이 그래프의 모양이 서로 달라도 동형 그래프일 수 있다.
- 그래프의 모든 정점들이 다른 정점들과 인접할 경우 완전 그래프(complete graph)라 한다.
- 그래프의 정점들을 2개의 집합 V1, V2으로 분할했을 때, 모든 변들이 V1의 정점과 V2의 정점을 인접시킬 경우 이를 이분 그래프(bipartite graph)라고 한다.
- 이분 그래프를 다르게 표현하면, 그래프의 정점을 두 가지 색으로 칠할 때 모든 변의 양 정점이 서로 다른 색으로 칠해질 수 있는 그래프라 할 수 있다.
- 홀수의 길이를 가지는 사이클은 이분 그래프가 될 수 없다.
- 이분 그래프 G=(V,E)에서 V가 V1과 V2로 분할되고, V1의 모든 정점과 V2의 모든 정점이 변으로 인접되어 있을 때, G를 완전 이분 그래프(complete bipartite graph)라 한다. V1의 정점의 개수가 m이고 V2의 정점의 개수가 n이라면 Km,n으로 표기한다.
- 그래프 G=(V,E)의 모든 정점들이 동일한 수의 인접한 정점을 가질 경우 정규 그래프(regular graph)라 한다. 정규 그래프의 모든 정점들은 동일한 차수를 가지게 되는데, 특히 각 정점의 차수가 k라면 k-정규 그래프라고 부른다.
발생, 인접, 연결의 차이
- 변 e가 정점 v, w를 연결하고 있을 때 v와 w는 e에 의해 발생되었다 또는 부수되었다고 한다.
- 정점 v와 w가 단 하나의 변으로 직접 연결된 경우 서로 인접하다고 한다.
- 정점 v와 w가 하나의 경로(하나 이상의 변으로 이어질 수 있음)로 이어진 경우 서로 연결됐다고 한다.
트리와 그래프의 차이
- 그래프 이론의 관점에서 트리는 사이클이 없는 무방향 연결 그래프로 정의된다.
- 또한 트리를 사이클이 없는 방향 그래프(Directed Acyclic Graph, DAG)의 일종으로 보기도 한다.
- 따라서 트리는 사이클을 허용하지 않지만 그래프는 사이클을 허용한다.
- 트리의 모든 노드는 연결돼있어야 하지만 그래프에는 연결되지 않은 노드가 존재할 수 있다.
- 트리는 하나의 뿌리 노드에서 시작하여 모든 자식 노드는 뿌리 노드에 대해 계층적인 구조가 된다. 반면에 그래프에는 뿌리 노드가 존재하지 않는다.
- 트리는 단방향이고 항상 부모 노드에서 자식 노드 방향으로 연결된다. 반면에 그래프는 방향성이 있거나 없을 수 있고, 방향도 양방향 또는 단방향을 모두 허용한다.
- 트리에서 뿌리 노드를 제외한 모든 노드는 부모 노드를 하나만 가져야 하지만 그래프에선 부모 노드 개념이 없으므로 이러한 제한이 없다.
- 트리에서 노드의 차수는 그 노드가 가진 자식 노드의 개수를 의미하지만 그래프에서 노드의 차수는 그 노드에 인접한 노드의 개수를 의미한다.
그래프 ADT의 연산
- 밑에서 G는 그래프를 의미하며 x, y, z 등은 그래프 G에 속한 정점을 의미한다.
- adjacent(G, x, y): x에서 y로 연결된 간선이 있는지 확인한다.
- neighbors(G, x): x와 인접한 모든 정점의 리스트를 출력한다.
- add_vertex(G, x): x가 그래프에 없다면 x를 추가한다.
- remove_vertex(G, x): x가 그래프에 있다면 x를 삭제한다.
- add_edge(G, x, y, z): x와 y를 연결하는 간선이 없다면 간선 z를 추가한다.
- remove_edge(G, x, y): x와 y를 연결하는 간선이 있다면 그 간선을 삭제한다.
- get_vertex_value(G, x): x의 값을 반환한다.
- set_vertex_value(G, x, v): x의 값을 v로 설정한다.
- 가중 그래프의 연산:
get_edge_value(G, x, y): x와 y를 연결하는 간선의 가중치를 반환한다.
set_edge_value(G, x, y, v): 정점 x와 y를 연결하는 간선의 가중치를 v로 설정한다.
그래프의 표현 방법
- 그래프를 표현하려면 정점의 집합과 간선의 집합을 표현해야 한다.
- 정점의 집합은 배열이나 연결 리스트 등 어떤 자료구조를 사용하더라도 쉽게 표현할 수 있다.
- 그러나 간선의 집합은 정점 간의 인접 관계를 나타내야 하므로 표현이 까다롭다.
- 정점 간의 인접 관계를 나타내는 방법은 크게 행렬 또는 리스트를 이용하는 방법으로 나뉘는데, 행렬은 인접 행렬 또는 발생 행렬이 있고 리스트는 인접 리스트가 있다.
- 인접 행렬과 발생 행렬은 구현이 간단하고 인접 여부를 빠르게 알 수 있지만 메모리 사용량이 크다는 단점이 있고, 인접 리스트는 메모리 사용량이 적지만 정점들의 인접 여부를 알기 위해 순차 탐색을 해야 한다는 단점이 있다.
인접 행렬(adjacency matrix)
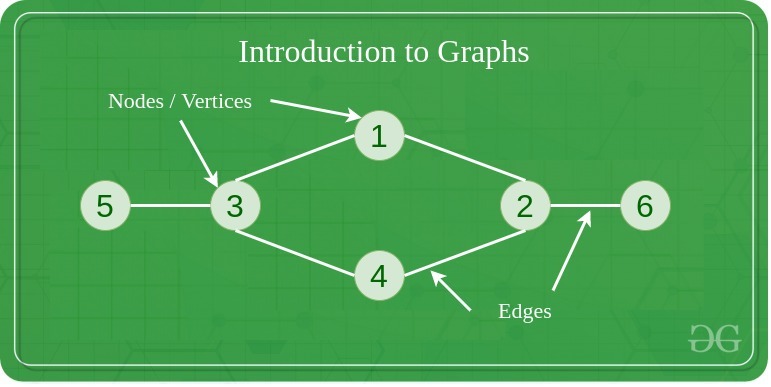
- 인접 행렬은 정점과 정점 간의 인접 관계를 나타내는 행렬이다.
- 그래프에 포함된 정점의 개수 N대로
N X N 크기의 정방행렬을 만들고, 각 정점이 서로 인접한 경우 행렬에서 1로 표시하고, 인접하지 않은 경우엔 0으로 표시한다.
| 정점 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|
| 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 1 | 0 | 1 |
| 3 | 1 | 0 | 0 | 1 | 1 | 0 |
| 4 | 0 | 1 | 1 | 0 | 0 | 0 |
| 5 | 0 | 0 | 1 | 0 | 0 | 0 |
| 6 | 0 | 1 | 0 | 0 | 0 | 0 |
- 무방향 그래프의 모든 정점에 루프나 병렬 변이 없다면 무방향 그래프의 인접 행렬은 위와 같이 대칭행렬이 된다.
- 방향 그래프에 대한 인접 행렬은 일반적으로 대칭행렬이 되지 않는다.
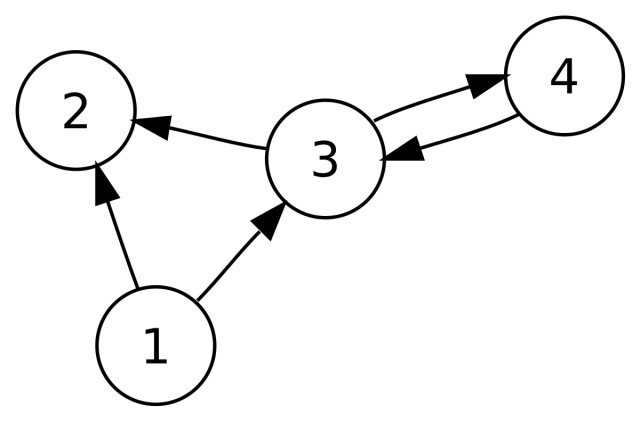
- 방향 그래프에선 간선이 가리키는 방향으로만 인접한 것으로 표현한다. 위의 방향 그래프를 인접행렬로 만들면 다음과 같다.
| 정점 | 1 | 2 | 3 | 4 |
|---|
| 1 | 0 | 1 | 1 | 0 |
| 2 | 0 | 0 | 0 | 0 |
| 3 | 0 | 1 | 0 | 1 |
| 4 | 0 | 0 | 1 | 0 |
- 가중 그래프의 경우 인접 관계가 있으면 가중치의 값을 표시하고 인접 관계가 없으면 무한대(∞)로 표시한다.
발생 행렬(근접 행렬, incidence matrix)
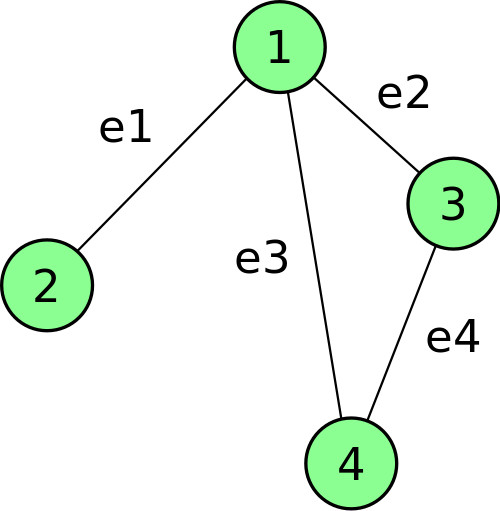
- 발생 행렬은 정점과 간선 간의 인접 관계를 나타내는 부울행렬이다.
정점의 개수 X 간선의 개수 크기의 행렬을 만들고 정점과 간선이 인접한 상태면 1, 아니면 0으로 표시한다.- 위의 무방향 그래프에 대한 발생 행렬을 표로 나타내면 다음과 같다.
| 정점/간선 | e1 | e2 | e3 | e4 |
|---|
| 1 | 1 | 1 | 1 | 0 |
| 2 | 1 | 0 | 0 | 0 |
| 3 | 0 | 1 | 0 | 1 |
| 4 | 0 | 0 | 1 | 1 |
인접 리스트(adjacency list)
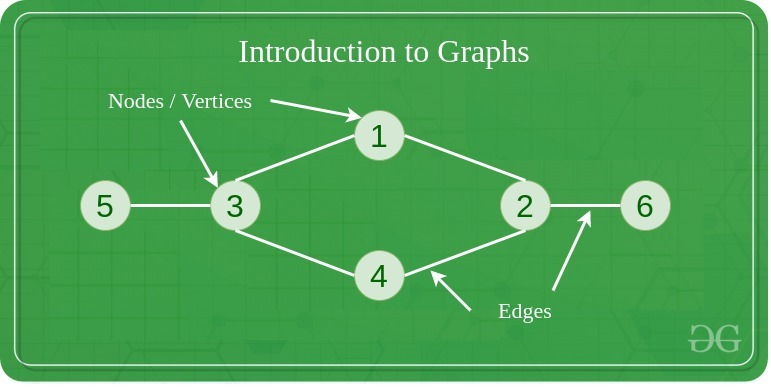
- 인접 리스트는 그래프 내 각 정점의 인접 관계를 표현하는 리스트이다. 일반적으로 연결 리스트로 구현한다.
- 각 정점이 인접한 모든 정점의 목록을 리스트로 만들어 관리한다.
- 위의 무방향 그래프에 대한 인접 리스트를 표로 나타내면 다음과 같다.
| 정점 | 인접한 정점 |
|---|
| 1 | 2, 3 |
| 2 | 1, 4, 6 |
| 3 | 1, 4, 5 |
| 4 | 2, 3 |
| 5 | 3 |
| 6 | 2 |
- 방향 그래프의 경우 인접 행렬과 마찬가지로 간선이 가리키는 방향으로만 인접한 것으로 표현한다.
- 가중 그래프의 경우 리스트에 간선의 가중치를 나타내는 필드를 추가해야 한다.
그래프의 탐색
- 그래프의 모든 변을 서로 교차하지 않게 그릴 수 있다면 평면 그래프(planar graph)라 한다.
- 다음은 평면 그래프와 평면 그래프가 아닌 경우의 예시이다.
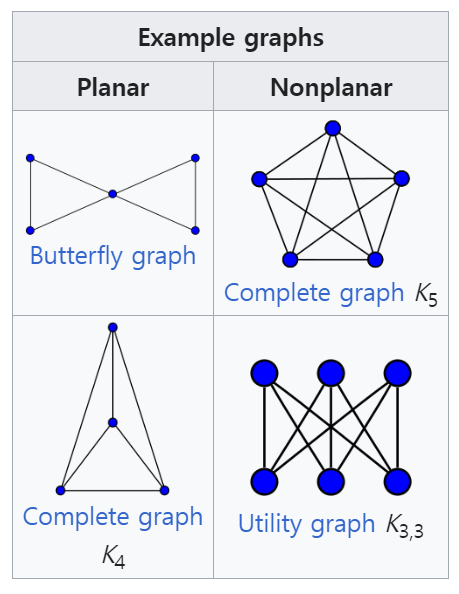
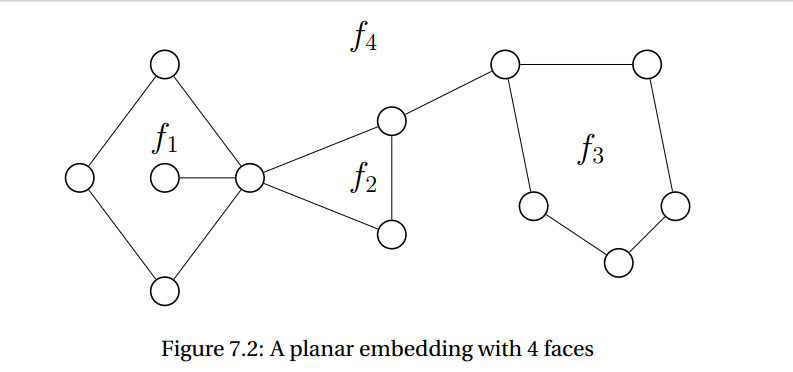
- 위 그림에서 f1,f2,f3 같이 변들의 사이클을 경계로 형성된 공간을 면(face)이라 한다. f4같이 그래프의 바깥 부분에 있는 것도 면에 포함된다.
오일러의 다면체 공식
- 수학자 오일러는 연결된 평면 그래프의 꼭지점, 변, 면의 수에 대한 공식을 정리했는데 이를 오일러의 다면체 공식(Euler's polyhedron formula)이라 하며 내용은 다음과 같다.
- 연결된 평면 그래프에서 꼭지점의 수를 v, 변의 수를 e, 면의 수를 f라 할 때
v−e+f=2이다.
4색정리
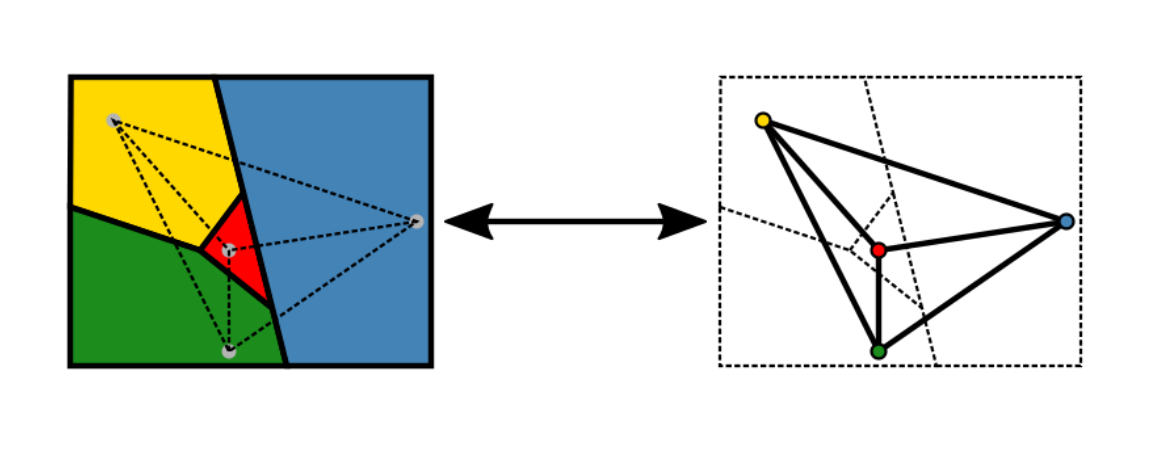
- 4색정리란 지도의 인접한 구획을 서로 다른 색으로 칠하려면 네 가지 색으로 충분하다는 정리이다.
- 모든 지도는 평면 그래프로 나타낼 수 있기 때문에 다음과 같이 4색정리를 평면 그래프에 대해 정의할 수 있다.
평면 그래프의 각 꼭지점에 대해 인접한 꼭지점과 다른 색으로 칠하는 데 필요한 색은 네 가지이면 충분하다.
오일러 트레일과 오일러 투어
- 그래프의 모든 변들을 각각 한 번만 지나는 트레일을 오일러 트레일(Eulerian trail) 또는 오일러 워크(walk)라 한다.
- 트레일에서 모든 변은 서로 달라야 하므로 오일러 트레일은 모든 변을 정확히 한 번만 지나가야 한다. 따라서 오일러 트레일을 한붓그리기라고도 부른다.
- 시작점과 종점이 동일한 오일러 트레일을 오일러 사이클(Eulerian cycle) 또는 오일러 회로(circuit) 또는 오일러 투어(tours)라 한다. 이는 닫힌 한붓그리기이다.
오일러 그래프 정리
- 오일러 투어(사이클, 회로)를 갖는 그래프를 오일러 그래프(Eulerian graph)라고 한다.
- 연결 그래프가 오일러 투어를 가지기 위한 필요충분조건은 그래프의 모든 꼭지점의 차수가 짝수인 것이다. 또한 이 명제의 역도 성립한다. 즉, 어떤 그래프가 오일러 그래프라면 이 그래프의 모든 꼭지점의 차수는 짝수이며 연결된 그래프이다.
해밀턴 경로와 해밀턴 사이클
- 그래프의 모든 꼭지점을 각각 한 번씩만 지나는 경로를 해밀턴 경로(Hamiltonian path)라 한다.
- 시작점과 종점이 같은 해밀턴 경로를 해밀턴 사이클(Hamiltonian cycle) 또는 해밀턴 회로(circuit)라고 한다.
- 어떤 그래프에 해밀턴 사이클이 존재한다면 해밀턴 경로도 존재하지만, 역은 성립하지 않는다.
그래프 순회(Graph Traversal)
- 그래프 순회란 그래프의 모든 정점을 방문하는 작업이다.
- 가장 대표적인 순회 방법으로 깊이 우선 탐색과 너비 우선 탐색이 있다.
깊이 우선 탐색(Depth First Search, DFS)
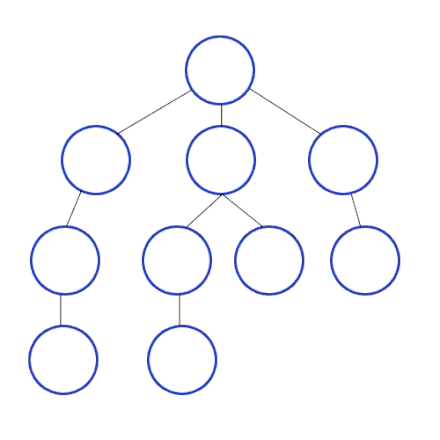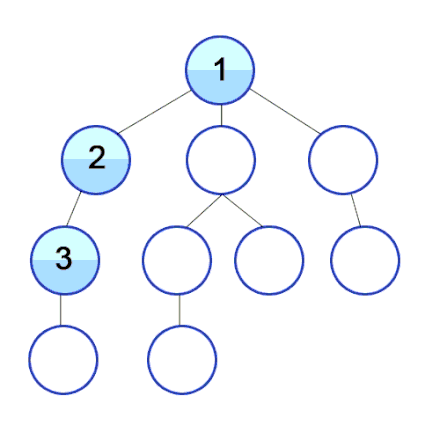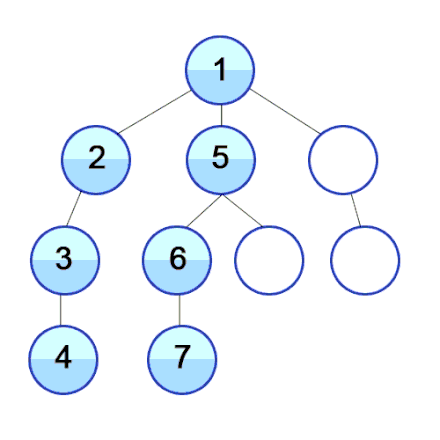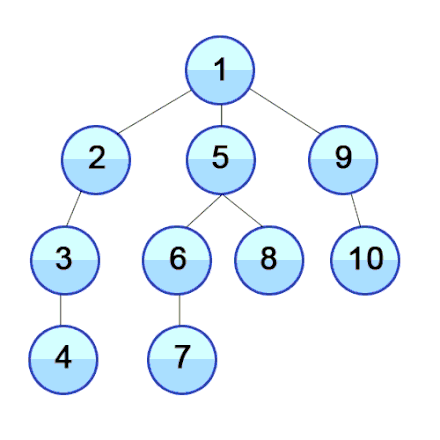
- 깊이 우선 탐색은 더 나아갈 길이 보이지 않을 때까지 깊이 들어가는 방법을 반복하여 그래프 내의 모든 정점을 방문하는 알고리즘이다. 일반적으로 그래프 순회를 위해서는 BFS 보단 DFS가 널리 쓰인다.
- DFS는 막다른 길이 나올 때까지 그래프의 정점들을 타고 깊이 들어가다가 방문한 정점 말고는 다른 이웃을 갖고 있지 않은 정점을 만나면 뒤로 돌아와 다른 경로로 뻗어 있는 정점을 타고 방문을 재개하는 방식으로 동작한다.
- 백트래킹(Backtracking) 알고리즘은 DFS와 관련이 있다.
- DFS는 주로 재귀호출 또는 스택을 활용한 반복문으로 구현할 수 있다.
- DFS를 스택을 사용하여 반복문으로 구현할 경우 탐색 과정은 다음과 같다.
- 탐색을 위한 스택 S와 방문한 정점을 담는 리스트 L을 만든다.
- 그래프의 시작 정점을 스택 S에 삽입한다.
- 스택 S에서 정점 하나(정점 v)를 추출(pop)한다. 따라서 맨 처음에는 시작 정점이 정점 v가 된다.
- 리스트 L에 정점 v가 없으면 다음의 두 가지 작업을 수행한다.
- 정점 v를 리스트의 맨 뒤로 삽입한다.
- 정점 v에 인접한 정점들을 모두 스택에 삽입한다.
- 스택 S가 빈 상태가 될 때까지 3번과 4번을 반복한다. 반복이 끝나면 리스트 L을 반환한다.
너비 우선 탐색(Breadth First Search, BFS)
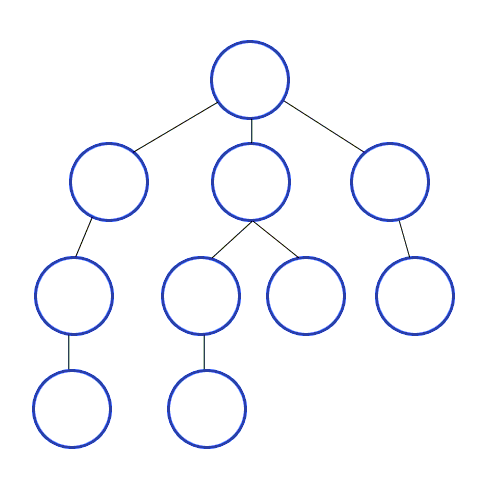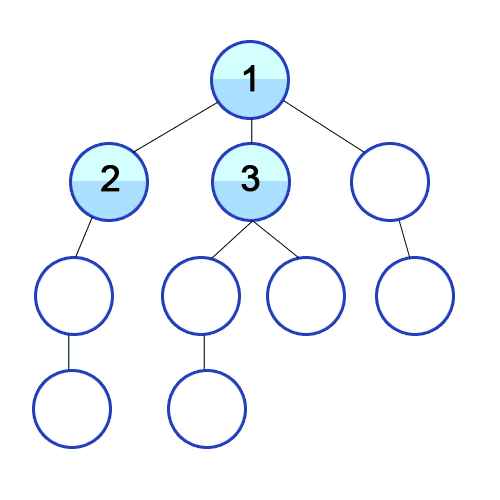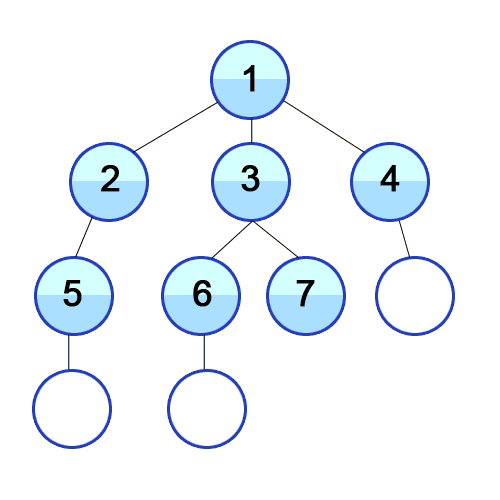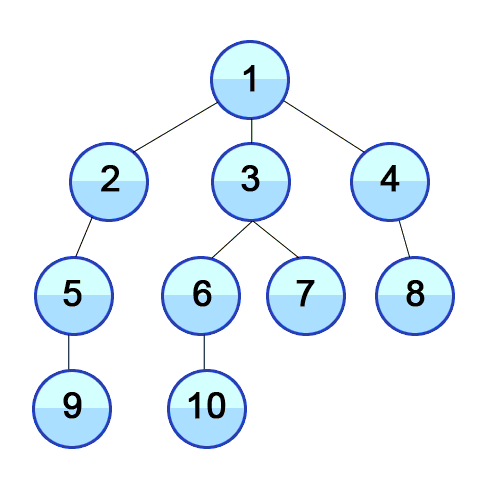
- 너비 우선 탐색은 시작 정점을 기준으로 깊이가 1인 모든 정점을 방문하고 그다음에는 깊이가 2인 모든 정점을 방문하는 식으로 한 단계씩 깊이를 더해가며 해당 깊이에 있는 모든 정점을 방문하는 알고리즘이다.
- BFS는 보통 큐를 활용하며 재귀가 아닌 반복문으로 구현한다.
- BFS의 탐색 과정을 구체적으로 설명하면 다음과 같다.
- 시작 정점을 방문했음(discovered) 리스트와 BFS을 위한 큐에 삽입한다.
- 큐에서 정점을 제거한다. 제거한 정점의 인접 정점 중에서 아직 방문하지 않은 곳을 방문했음 리스트와 큐에 삽입한다.
- 큐가 빈 상태가 될 때까지 2번을 반복한다. 반복이 끝나면 방문했음 리스트를 반환한다.
파이썬 DFS, BFS 예제 코드
graph = {
1: [2, 5, 9],
2: [1, 3],
3: [2, 4],
4: [3],
5: [1, 6, 8],
6: [5, 7],
7: [6],
8: [5],
9: [1, 10],
10: [9]
}
def recursive_dfs(v, discovered=[]):
discovered.append(v)
for w in graph[v]:
if w not in discovered:
discovered = recursive_dfs(w, discovered)
return discovered
def iterative_dfs(start_v):
discovered = []
stack = [start_v]
while stack:
v = stack.pop()
if v not in discovered:
discovered.append(v)
for w in graph[v]:
stack.append(w)
return discovered
def iterative_bfs(start_v):
discovered = [start_v]
queue = [start_v]
while queue:
v = queue.pop(0)
for w in graph[v]:
if w not in discovered:
discovered.append(w)
queue.append(w)
return discovered
print(recursive_dfs(1))
print(iterative_dfs(1))
print(iterative_bfs(1))
참고자료