그래프 심화 개념정리

개발자 강세영·2023년 11월 7일

MST 네트워크 플로 문제 데이크스트라 알고리즘 솔린 알고리즘 알고리즘 위상 정렬 자료구조 최소 신장 트리 칸의 알고리즘 크루스칼 알고리즘 포드-풀커슨 알고리즘 프림 알고리즘

TIL

목록 보기

65/70

그래프 이론의 주요 문제

그래프 이론의 대표적인 문제로는 위상 정렬, 최단 경로 문제, 최소 신장 트리 문제, 네트워크 플로 문제 등이 있다.
위상 정렬은 DAG에서 정점들을 간선의 방향을 거스르지 않도록 나열하는 것이다.
최단 경로 문제는 가중 그래프의 두 정점을 잇는 가장 짧은 경로를 찾는 문제이다.
최소 신장 트리 문제는 가중 그래프의 모든 정점들을 연결하면서 최소한의 가중치를 갖는 조합을 찾는 문제이다.
네트워크 플로 문제는 그래프의 일종인 네트워크(network)상에서의 흐름(flow)을 찾는 문제이다.

위상 정렬(Topological Sorting)

그래프에서 위상(topology)이란 어떤 정점이 다른 정점과의 관계 속에서 가지는 위치를 의미한다.
그래프를 위상 정렬하려면 그래프에 방향성이 있으면서 사이클이 없어야 한다. 이러한 그래프를 DAG(Directed Acyclic Graph)라고 한다.
위상 정렬은 DAG의 정점들을 방향성을 거스르지 않도록 선형적으로 나열하는 것이다. DAG에는 적어도 하나 이상의 위상 순서가 있다.
그래프의 정점은 수행할 작업을 나타낼 수 있고, 간선은 한 작업이 다른 작업보다 먼저 수행되어야 한다는 제약 조건을 나타낼 수 있다.
위상정렬의 좋은 예로 대학의 선수과목 구조가 있다. 만약 특정 수강과목에 선수과목이 있다면 그 선수과목부터 수강해야 하므로, 특정 과목들을 수강해야 할 때 위상 정렬을 통해 올바른 수강 순서를 찾아낼 수 있다.
이와 같이 선후 관계가 정의된 그래프 구조 상에서 그 관계에 따라 정렬하는 작업이 바로 위상 정렬이다.
위상 정렬을 위해서는 간선을 두 가지 종류로 구분해야 하는데 하나는 정점으로 들어가는 진입(incoming) 간선이고, 다른 하나는 정점에서 나가는 진출(outgoing) 간선이다.
위상 정렬을 위한 알고리즘으로는 칸의 알고리즘, DFS, 병렬(parallel) 알고리즘 등이 있다.
일반적으로 위상 정렬의 시간 복잡도는 그래프의 정점의 개수(V)에 간선의 개수(E)를 더한 선형 시간이 되는데, 빅 오 표기법으로 표현하면 다음과 같다. $O(|V|+|E|)$

칸의 알고리즘(Kahn's algorithm)

Arthur B. Kahn이 1962년에 발표한 위상 정렬 알고리즘이다.
알고리즘의 수행 과정은 다음과 같다.
L: 정렬된 정점들을 담을 리스트, S: 진입 간선이 없는 정점들의 집합
1. 진입 간선이 없는 시작 정점들을 모두 S에 삽입한다. DAG에는 시작 정점이 반드시 하나 이상 존재한다.
2. S의 한 정점 n을 제거하고, 이 정점 n을 L에 삽입한다.
3. 정점 n에서 정점 m으로 연결된 간선 e(진출 간선)를 제거한다.
4. 정점 m이 진입 간선이 없는 정점이면 S에 m을 삽입한다.
5. S가 빈 상태가 될 때까지 2~4번을 반복한다.
6. 이후에 그래프에 간선이 남아 있다면 그래프에 사이클이 있다는 의미이므로 에러를 반환한다.
  그래프에 간선이 모두 제거됐다면 L을 반환한다.

DFS를 이용한 위상 정렬

칸의 알고리즘이 그래프의 시작점을 정해서 끝까지 순서대로 정렬하는 방식이라면, DFS를 이용한 위상 정렬은 먼저 DFS 탐색으로 그래프의 깊은 곳을 찾고 그로부터 출발하여 위로 올라오는 방식으로 진행된다.
DFS를 이용한 위상 정렬 과정은 다음과 같다.
1. 위상 정렬을 위한 리스트 L을 준비한다.
2. 그래프에서 진입 간선이 없는 정점에 대해 DFS를 시행하고, 탐색 중에 인접 정점이 없는 정점을 만나면 이 정점을 L의 맨 앞에 삽입한다.
3. 더 이상 방문할 정점이 없으면 DFS를 종료하고 L을 반환한다.

최단 경로 문제(shortest path problem)

최단 경로 문제는 가중 그래프에서 주어진 조건을 충족하는 가장 짧은 경로를 찾는 문제이다.
최단 경로 문제는 출발점과 도착점의 유형에 따라 단일 쌍 최단 경로 문제, 단일 출발점 최단 경로 문제, 단일 도착점 최단 경로 문제, 전체 쌍 최단 경로 문제로 구분된다.
- 단일 쌍(single-pair): 그래프의 한 출발점에서 한 도착점까지의 최단 경로를 찾는 문제이다. 즉, 출발점과 도착점을 미리 정해놓고 이를 연결하는 최단 경로를 찾는 방식이다.
- 단일 출발점(single-source): 출발점 v에서 다른 모든 정점들에 대한 최단 경로를 찾는 문제이다. 즉, 출발점만 정해놓고 이 출발점에서 다른 모든 도착점에 대해 최단 경로를 찾는 방식이다.
- 단일 도착점(single-destination): 모든 정점으로부터 출발하여 그래프 내의 단일한 도착점 v로 도착하는 최단 경로를 찾는 문제이다. 즉 단일 출발점 문제를 뒤집은 것이다.
- 전체 쌍(all-pairs): 그래프 내의 모든 정점 쌍들 사이의 최단 경로를 구하는 문제이다.
최단 경로 문제에 대한 알고리즘으로는 데이크스트라 알고리즘, 벨만-포드 알고리즘, 플로이드-워셜 알고리즘, A* 탐색 알고리즘 등이 있다.

데이크스트라 알고리즘(Dijkstra's algorithm)

데이크스트라 알고리즘은 에츠허르 데이크스트라가 개발한 알고리즘으로, 가중 그래프에서 단일 출발점(single-source) 최단 경로를 찾는 알고리즘이다.
데이크스트라 알고리즘은 그리디(greedy) 알고리즘과 동적 계획법(dynamic programming)에 기반하며, 최소 신장 트리를 찾는 프림 알고리즘(Prim's Algorithm)과 매우 유사하다.
데이크스트라 알고리즘은 활용하는 자료구조나 로직에 의한 여러 가지의 변형이 있다.
일반적인 구현은 음의 가중치를 허용하지 않으면서(non-negative) 사이클이 없는 방향 그래프에 대한 것이다.
기본적인 데이크스트라 알고리즘의 수행과정은 다음과 같다.
입력: 가중 그래프 G, 출발점 s
출력: s로부터 다른 정점으로의 현재 길이를 담는 배열 dist[], s로부터 다른 정점으로의 최단 경로를 만드는 선행 정점들을 담는 배열 prev[]
1. 그래프의 모든 정점에 대해 반복적으로 다음 초기화 작업을 수행한다.
  - dist[]의 요소들을 모두 무한대로 초기화 한다. 단 출발점에 대한 값 dist[s]는 0으로 초기화 한다.
  - prev[]의 요소들을 모두 정의되지 않은 값(undefined, null 등)으로 초기화한다.
  - 공집합 Q에 그래프의 모든 정점을 삽입한다.
2. Q가 빈 상태가 될 때까지 다음을 반복한다.
  - Q의 정점 중 dist[]가 최소값인 정점 u를 Q에서 제거한다. 위에서 초기화한 결과에 의해 첫 번째 u는 시작 정점 s가 된다.
  - 정점 u에 인접한 모든 정점 v에 대해 정점 u를 경유해서 v에 이르는 거리가 기존 거리보다 작으면 새로운 거리값으로 조정하고 정점 v의 선행 정점을 u로 지정한다. 이 단계에서 위에서 초기화한 배열 dist[]와 prev[]의 요소들이 변경된다.
3. 2번이 완료된 후 배열 dist[]와 prev[]를 반환한다.
데이크스트라 알고리즘의 시간 복잡도는 집합 Q를 나타내기 위한 자료구조에 따라 달라진다.
Q를 인접 행렬 또는 인접 리스트로 구현하면 시간 복잡도는 $Θ(|V|^2)$ 가 된다.
Q를 자가 균형 이진 탐색 트리, 이진 힙, 피보나치 힙, 우선순위 큐 등으로 구현하면 ${\ \Theta ((|E|+|V|)\log |V|)}$ 또는 ${\ \Theta (|E|+|V|\log |V|)}$ 이 된다.

벨만-포드 알고리즘(Bellman–Ford algorithm)

이 알고리즘은 알폰소 심벨(Alfonso Shimbel)에 의해 처음 제안됐지만, 리차드 벨만과 레스터 포드가 발표한 논문에 의해 알려져 벨만-포드 알고리즘이라고 부른다. 후에 에드워드 무어가 이 알고리즘을 보완하는 논문을 발표하여 벨만-포드-무어 알고리즘이라고도 한다.
이 알고리즘은 음의 가중치를 갖는 그래프에서도 단일 출발점 최단 경로를 구할 수 있지만 그래프에 음의 사이클이 존재하면 적용할 수 없다.
알고리즘의 수행과정은 다음과 같다.
1. 데이크스트라 알고리즘과 비슷하게 dist와 prev 배열에 대한 초기화 작업을 수행한다.
2. 1부터 정점의 개수 - 1 만큼 반복하는 루프를 만든다. 따라서 처음에는 간선 1개만을 사용하는 최단 경로가 계산되고 다음 반복에는 간선 2개, 3개, ... 이런식으로 반복되어 마지막에는 정점의 개수 - 1 만큼의 간선을 사용하는 경로가 계산된다.
3. 2번 루프의 안쪽에서 간선 집합 E의 모든 간선 (u, v), 그 간선의 가중치 w에 대해 다음을 반복한다.
- dist[u] + w < dist[v]이면 dist[v] = dist[u] + w, prev[v] = u 로 변경한다.
- 이 부분 또한 데이크스트라 알고리즘과 비슷하다.
1. 2, 3번 루프가 완료되면 음의 사이클이 존재하는지 확인해야 한다.
- 간선 집합 E의 모든 간선 (u, v)에 대해 dist[u] + w < dist[v]인 경우가 나오면 그래프에 음의 사이클이 있으며 해가 없다는 의미이므로 오류를 반환한다.
- 음의 사이클이 없다면 정상적인 경우이므로 dist[]와 prev[]를 반환한다.
이 알고리즘의 최악의 시간 복잡도는 $O(|V||E|)$ 로 일반적으로 데이크스트라 알고리즘보다 비효율적이지만 음의 가중치를 갖는 그래프에 대해서 활용할 수 있다는 장점이 있다.

플로이드-워셜 알고리즘(Floyd–Warshall algorithm)

데이크스트라 알고리즘과 벨만-포드 알고리즘은 단일 출발점 최단 경로를 구하는 알고리즘이지만 플로이드-워셜 알고리즘은 전체 쌍(all-pairs) 최단 경로를 찾기 위한 알고리즘이다.
스테픈 워셜이 방향 그래프에서 정점들 간의 상호 연결 경로의 존재 여부를 판단하는 알고리즘을 개발하였고 이를 로버트 플로이드가 최단 경로를 구하는 알고리즘으로 변형한 것이 바로 플로이드-워셜 알고리즘이다.
이 알고리즘은 인접 행렬을 활용하며 동적 프로그래밍에 기반하는 알고리즘이다. 수행과정은 다음과 같다.
1. 초기화 작업을 수행한다.
- |V| x |V| 크기의 정방행렬(2차원 배열) dist를 만들고 값은 모두 무한대로 초기화 한다.
- 모든 간선 (u, v)에 대해 dist[u][v] 값을 간선 (u, v)의 가중치로 바꾼다.
- 모든 정점 v에 대해 dist[v][v] 값을 0으로 바꾼다.
1. 모두 정수 0에서 정점의 개수 - 1까지 똑같이 반복하는 삼중 반복문을 만든다. (k->i->j)
- 가장 안쪽인 j 루프에서 다음과 같이 dist배열의 값을 바꾸는 작업을 수행한다.
  dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])
1. 반복문이 종료되면 dist 배열을 반환한다.
위의 구현으로는 최단 경로의 길이만 구할 수 있다. 최단 경로의 순서를 구하려면 선행 정점들을 담을 prev 배열을 추가하여 구현하면 된다.
이 알고리즘의 시간 복잡도는 $O(|V|^3)$ 이다.

최소 신장 트리(Minimum Spanning Tree, MST)

신장 트리(spanning tree)는 무방향 그래프의 모든 정점과 간선의 일부(또는 전부)를 포함하는 트리이다.
그래프의 모든 정점과 이 정점들을 연결하는 간선이 포함되므로 그래프는 연결된 상태(connected)이며 사이클(cycle)이 없어야 한다.
그래프에서 정점의 개수가 n일 때, 신장 트리는 n-1개의 간선을 사용해서 모든 정점을 연결시킨 부분 그래프이다.
최소 신장 트리는 최소 가중치 신장 트리(minimum weight spanning tree)라고도 하는데,
여러 간선 중 가중치의 합이 최소가 되는 간선만 남긴 신장 트리가 바로 최소 신장 트리이다.
따라서 최소 신장 트리는 무방향의 연결된 가중 그래프로부터 만들 수 있고 이러한 그래프에서 위의 조건을 만족하는 부분 그래프는 최소 신장 트리가 된다.
최소 신장 트리는 군집 분석, 각종 네트워크 문제, 회로 설계, 컴퓨터 비전 등 다양한 분야에서 활용된다.
주어진 그래프로부터 최소 신장 트리를 만드는 알고리즘으로는 프림 알고리즘, 크루스칼 알고리즘, 솔린 알고리즘 등이 있다.

프림 알고리즘(Prim's Algorithm)

로버트 프림이 개발한 MST 알고리즘으로 수행 과정은 다음과 같다.
1. 빈 MST를 준비한다.
2. 그래프에서 임의의 정점을 시작 정점으로 선택하여 MST의 뿌리 노드로 삽입한다.
3. MST에 삽입된 정점들과 이 정점들의 모든 인접 정점 사이에 있는 간선의 가중치를 조사하여 이중에서 가중치가 가장 작은 것을 골라 이 간선에 연결된 인접 정점을 MST에 삽입한다.
  단, 새로 삽입되는 정점이 MST 안에서 사이클을 만들지 않도록 한다.
4. 3번을 반복하다가 MST가 그래프의 모든 정점을 연결하게 되면 종료한다.
프림 알고리즘에선 MST를 위해 어떤 자료구조를 활용할 것인지와 최소 가중치 간선을 찾는 방법이 중요하다.
일반적으로 MST를 위한 자료구조로 우선순위 큐를 활용하는데, 삽입과 삭제가 빠르고 최소값을 쉽게 찾을 수 있기 때문이다.
프림 알고리즘의 시간 복잡도를 정리하면 다음과 같다. (최소 가중치 간선에 대한 자료구조: 시간 복잡도)
인접 행렬, 탐색: $O(|V|^2)$
이진 힙, 인접 리스트: $O(|E|log|V|)$
피보나치 힙, 인접 리스트: $O(|E| + |V|log|V|)$
프림 알고리즘의 간단한 예시.

크루스칼 알고리즘(Kruskal's Algorithm)

조셉 크루스칼이 개발한 MST 알고리즘이다.
프림 알고리즘이 MST에 연결된 정점들의 가중치를 단계적으로 확인하며 완성해나가는 방법이라면, 크루스칼 알고리즘은 그래프 내 모든 간선의 가중치를 사전에 파악하고 이 정보를 토대로 MST를 구축해나가는 방법이다.
크루스칼 알고리즘의 수행 과정은 다음과 같다.
1. 그래프 내의 모든 간선을 가중치의 오름차순으로 정렬한 목록을 만든다.
2. 1번에서 만든 간선의 목록을 차례대로 순회하면서 간선을 MST에 추가한다. 단, 이때 추가된 간선으로 인해 MST내에 사이클이 형성되면 안된다.
어떤 간선을 MST에 추가할 때 MST에 사이클이 형성되는지를 판단하는 것이 크루스칼 알고리즘에서 가장 중요한 문제가 된다.
사이클 여부를 판단하기 위해 깊이 우선 탐색(DFS)을 이용할 수 있다. DFS로 방문한 정점들을 방문했음으로 표시하여 사이클이 되는지 판단하는 방법이다. 이 방법은 탐색 비용이 크다는 문제가 있다.
DFS에 대한 대안으로 분리 집합을 이용하는 방법이 있다. 우선 각 정점별로 분리 집합을 만들고, 간선으로 연결된 정점들에 대해서는 합집합을 수행한다. 이때 간선으로 연결한 두 정점이 같은 집합에 속해 있다면 이 연결은 사이클을 이루게 되는 것으로 판단하는 방법이다.
크루스칼 알고리즘의 시간 복잡도는 $O(|E|log|V|)$ 이다.
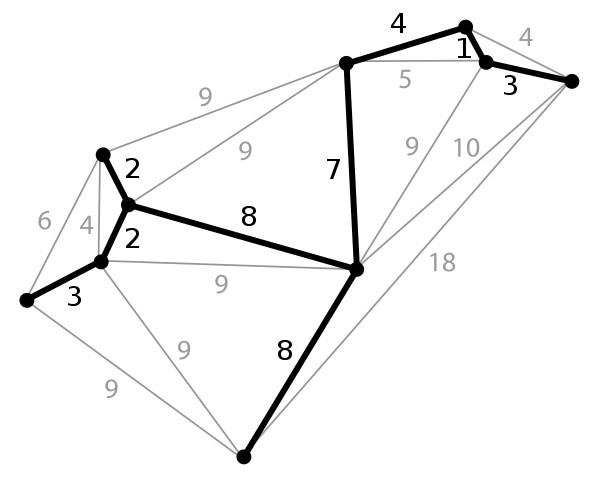
크루스칼 알고리즘 예시

솔린 알고리즘(Sollin's Algorithm)

Otakar Borůvka가 1926년에 처음 발표하였고, 1965년에 조르주 솔린(Georges Sollin)이 병렬화에 적합하도록 정리하여 솔린 알고리즘 또는 보르프카의 알고리즘이라고 한다.
그리디 알고리즘에 기반하여 MST를 찾는 알고리즘이다.
프림 알고리즘과 크루스칼 알고리즘은 각 단계마다 하나의 간선을 선택하지만 솔린 알고리즘은 다수의 간선을 선택하는 방식이므로 병렬성이 우수하다.
이 알고리즘의 수행 과정은 다음과 같다.
1. 그래프의 간선은 제외하고, 정점으로만 구성된 숲(forest)을 만든다.
2. 1번에서 만든 숲 내의 트리들을 최소 비용을 갖는 간선으로 연결한다.
3. 남은 간선이 없거나 완전한 트리가 생성될 때까지 2번을 반복한다.
솔린 알고리즘의 시간 복잡도는 $O(|E|\log |V|)$ 이다.
솔린 알고리즘 예시

네트워크 플로 문제(Network flow problem)

그래프 이론에서 네트워크(flow network, transportation network, network graph)란 각각의 간선에 정해진 용량(capacity)과 용량 보다 같거나 작은 흐름(flow)이 있는 방향 그래프를 의미한다.
네트워크는 수학적으로 다음과 같이 5-튜플로 정의한다. $N=(V,E,s,t,c)$
여기서 V는 정점, E는 간선, s는 소스, t는 싱크, c는 간선의 용량을 의미한다.
네트워크에서 용량은 음의 값을 가질 수 없다.
네트워크에서 유출되는 흐름만 있는 정점은 소스(source), 유입되는 흐름만 있는 정점은 싱크(sink)라고 한다. 소스는 출발점, 싱크는 도착점과 비슷하다.
소스와 싱크를 제외한 모든 정점은 해당 정점에 유입되는 흐름의 총합과 유출되는 흐름의 총합이 같아야한다.
흐름(flow, 플로)이란 간선의 용량 중에서 실제 사용하고 있는 양 또는 값을 의미한다.
네트워크 플로 문제를 통해 도로망에서 차량의 흐름, 송유관에서의 기름의 흐름, 온라인 네트워크 상에서의 데이터의 흐름 등 다양한 문제를 모델링하고 최적화할 수 있다.
네트워크는 방향 그래프이지만 주어진 방향대로만 흐름을 계산해야하는 것은 아니며 필요하다면 역방향의 흐름도 계산할 수 있다.
네트워크 플로 문제란 주어진 네트워크에서 특정 조건을 만족하는 흐름을 찾는 문제로 다음과 같은 종류가 있다.
- 최대 흐름 문제(maximum flow problem): 가장 대표적인 네트워크 플로 문제로, 네트워크에서 흐름의 총량을 최대화하는 방법을 찾는 문제이다. 즉, 소스에서 나가는 플로의 합 또는 싱크로 들어오는 흐름의 합의 최대값을 구하는 문제이다.
- 최소 비용 흐름 문제(minimum-cost flow problem): 비용을 최소화 하면서 조건을 만족하는 흐름을 찾는 문제이다.
- 다품종 흐름 문제(multi-commodity flow problem): 서로 다른 소스 노드와 싱크 노드 사이에 여러 상품(흐름 수요)이 있는 문제이다.

포드-풀커슨 알고리즘(Ford–Fulkerson algorithm)

포드-풀커슨 알고리즘은 레스터 포드와 델버트 풀커슨이 개발한 그리디 기반 알고리즘으로 네트워크에서 최대 흐름을 구하는 가장 기초적인 알고리즘이다.
이 알고리즘은 단순하게 플로 값을 증가시킬 수 있는 모든 경우의 수를 탐색하는 방식으로 최대값을 찾는다.
관점에 따라 이 알고리즘은 알고리즘의 조건(유한성 등)을 충족하지 못하기 때문에 알고리즘이 아닌 포드-풀커슨 메서드(method)라고 부르기도 한다.
s에서 t까지 플로를 보내기 위한 경로를 증가 경로(augmenting path)라고 하며, 증가 경로 상의 간선은 네트워크 상의 간선의 방향과 반드시 일치하지는 않는다.
증가 경로의 간선이 네트워크의 간선과 방향이 같으면 순방향 간선(forward edge)라고 하며, 방향이 같지 않으면 역방향 간선(backward edge)이라고 한다.
순방향 간선에 대해 간선의 용량에서 실제 사용되는 플로를 뺀 값을 잔여 용량(residual capacity)이라고 한다.
역방향 간선의 잔여 용량은 순방향 간선의 플로와 같은 값이 된다.
순방향 간선의 잔여 용량은 해당 간선에 대해서 플로를 실제로 증가시킬 수 있는 값으로 사용되지만, 역방향 간선의 잔여 용량은 원래 간선에 부여된 플로를 줄일 수 있는 값으로 사용된다.
포드-풀커슨 알고리즘은 모든 경우의 수를 탐색하는 알고리즘이므로 역방향 간선에 대해서도 플로 값을 구해야한다.
이 알고리즘의 수행과정을 요약하면 증가 경로가 더 이상 존재하지 않을 때까지 반복적으로 증가 경로를 찾고, 이 증가 경로의 여유량만큼씩 플로 값을 증가시켜 최대 플로를 구하는 방법이라 할 수 있다.
수행과정을 구체적으로 설명하면 다음과 같다.
1. 모든 간선의 흐름을 0으로 초기화한다.
2. DFS를 이용하여 네트워크에서 증가 경로를 찾는다.
3. 증가 경로에서 잔여 용량의 최소값을 찾아 해당 양만큼 현재 흐름 값에 더하거나 뺀다. 순방향 간선의 경우 현재 흐름에 최소값을 더하면 되고 역방향 간선의 경우 현재 흐름에 최소값을 빼주면 된다.
4. 더 이상 증가 경로를 찾을 수 없을 때까지 2, 3번을 반복한다. 이 과정에서 네트워크의 모든 증가 경로를 사용하여 최대 흐름을 구하게 된다.
5. 4번까지 완료하면 소스에서 나가는 흐름의 합 또는 싱크로 들어오는 흐름의 합이 최대 흐름이 된다.
네트워크의 모든 용량이 정수인 경우 최대 흐름의 값은 증가 경로를 하나 찾을 때마다 최소 1씩 증가하므로 증가 경로는 항상 최대 흐름 값 이내로 찾게 된다. 하나의 증가 경로를 구하는 시간 복잡도는 $O(|E|)$ 이므로 시간 복잡도는 $O(|E|F)$ 가 된다. 여기서 $|E|$ 는 간선의 개수, $F$ 는 최대 흐름을 의미한다
포드-풀커슨 알고리즘에선 간선의 용량이 무리수인 경우 알고리즘의 종료가 보장되지 않는다. 또한 다음 그림과 같이 네트워크에서 간선의 용량 차이가 매우 큰 경우 수행시간이 비효율적이라는 문제가 있다.
다음의 네트워크 예시는 간단한 형태임에도 불구하고 경로를 2000번이나 탐색해야 최대 흐름을 구할 수 있다. 가운데에 위치한 1의 흐름에 대해 계산하는 것을 반복해야 하기 때문이다.
이러한 단점을 보완하기 위해 잭 에드먼즈와 리처드 카프에 의해 에드먼즈-카프 알고리즘(Edmonds–Karp algorithm)이 제시되었다.
에드먼즈-카프 알고리즘은 기본적으로 포드-풀커슨 알고리즘과 비슷하지만 증가 경로를 찾을 때 검색 순서가 정해진다는 점이 다르다.
에드먼즈-카프 알고리즘에선 먼저 BFS를 활용하여 s에서 t까지의 최단 경로를 구하고 이를 증가 경로로 사용한다.
이렇게 하면 간선의 용량과 상관없이 시간 복잡도는 $O(|V||E|^{2})$ 이 된다.