힙(Heap) 개념정리

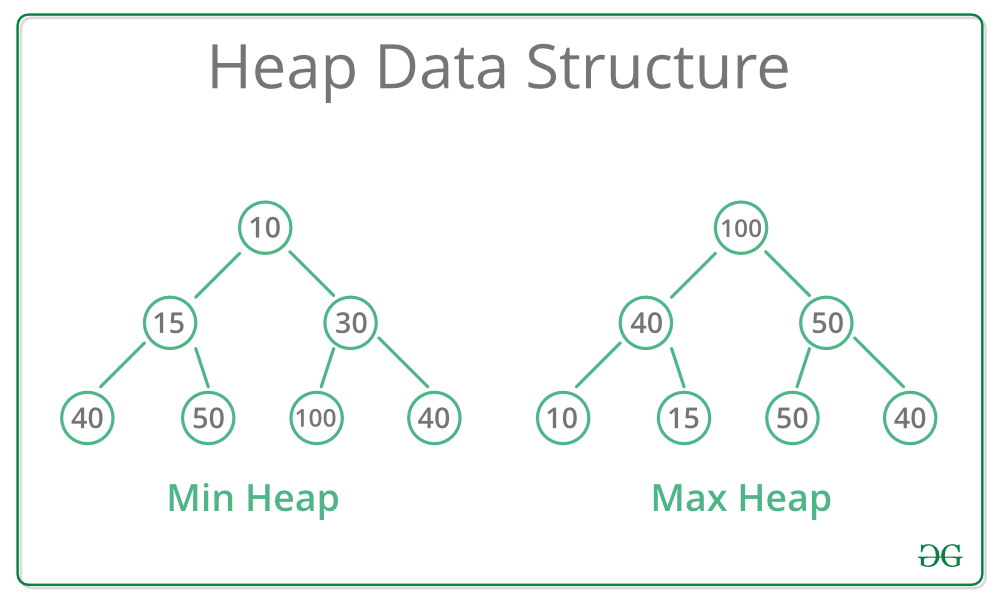
힙(Heap)이란?

• 영단어 heap은 물건들을 차곡차곡 쌓아올린 더미를 의미한다.
• 동적으로 할당되는 메모리 영역인 힙 영역(heap segment)과 자료구조 힙은 서로 이름이 같지만 아무 관련이 없다.
• 힙은 힙 속성을 충족하는 트리 기반의 자료구조이다.
• 다양한 종류의 힙이 존재하지만 보통 힙이라고 하면 힙 속성을 만족하는 완전 이진트리, 즉 이진 힙(binary heap)을 의미한다.
• 힙은 그 속성에 따라 최대 힙 또는 최소 힙으로 구분된다.
• 최대 힙은 부모 노드의 값이 항상 자식 노드의 값 보다 크거나 같다.
• 최소 힙은 그 반대로, 부모 노드의 값이 항상 자식 노드의 값 보다 작거나 같다.
• 따라서 최대 힙의 뿌리 노드는 항상 힙의 최대값이 되며 최소 힙의 뿌리 노드는 항상 힙의 최소값이 된다.
• 힙에서 자식 노드들의 값에 대해선 순서를 따지지 않는다. 따라서 같은 레벨의 노드들은 느슨한 정렬 상태를 갖는다.
• 힙은 데이터의 중복을 허용한다.
• 힙과 우선순위 큐는 서로 관련이 깊은데, 우선순위 큐 ADT를 효율적으로 구현한 것이 바로 힙이다.
• 힙은 최소 혹은 최대 값을 가지는 객체를 반복적으로 제거하거나, 루트 노드를 제거하면서 새 노드를 삽입하는 작업을 효율적으로 할 수 있다.

힙의 연산과 구현

• 힙에서 가장 중요한 연산은 최대값 또는 최소값 반환(top 또는 peek), 요소의 삽입(push), 뿌리 노드 삭제(pop), 뿌리 노드 교체(replace)이다.

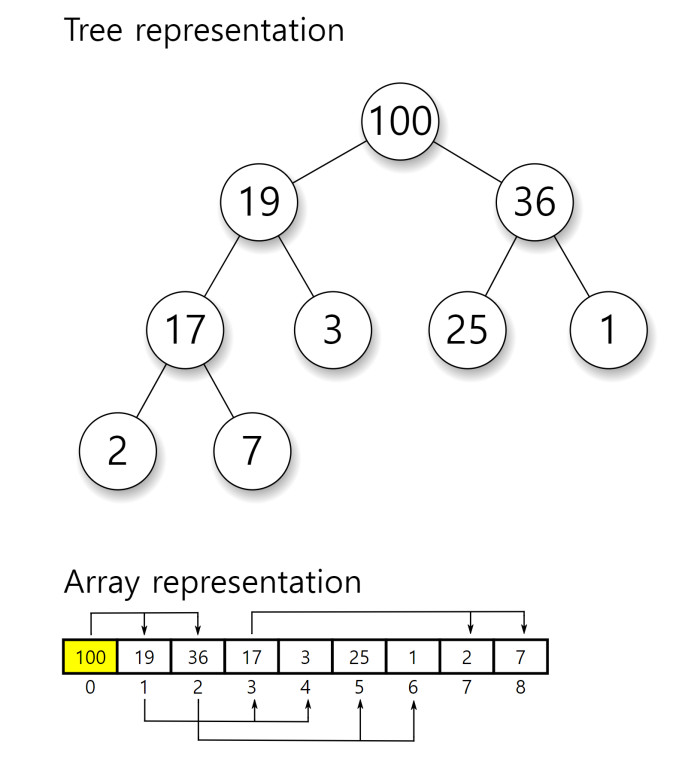
• 힙의 연산은 자식 노드와 부모 노드의 위치를 계산하는 것이 중요하다. 위 그림과 같이 배열로 힙을 나타내면 인덱스로 이러한 작업을 쉽게 수행할 수 있기 때문에 대개 힙 구현을 위한 자료구조로 연결 리스트보단 배열이 선호된다.

• 힙의 구현을 위해선 정적 배열 보다는 요소의 삽입과 삭제에 대응하여 용량을 조절할 수 있는 동적 배열이 적합하며 대개 배열의 현재 크기(size, 배열에 있는 요소의 개수)와 용량(capacity)을 관리하는 변수를 활용한다.

• 힙의 뿌리 노드는 배열의 맨 앞에 위치하며 자식 노드는 바로 다음 위치에 오는 식으로 배치된다.

• 힙에서 최대값 또는 최소값을 반환하는 연산은 배열의 첫 요소에 접근하는 것과 같으므로 시간 복잡도는 항상 $O(1)$이 된다.

• 힙에서 요소를 삽입하는 과정은 다음과 같다. 시간 복잡도는 $O(log n)$이다.

  1. 완전 이진트리의 모양을 유지하면서, 힙의 가장 깊은 곳의 맨 우측에 새 노드를 추가한다. 배열로 구현한 경우 배열의 끝에 삽입하면 된다.
  2. 삽입한 노드가 부모 노드보다 크거나 작은지 비교한다. 삽입한 노드가 제 위치에 있다면 연산을 종료한다.
  3. 적절한 위치가 아니라면 부모 노드와 삽입한 노드의 위치를 서로 바꾸고 2번으로 돌아가 반복한다.

• 힙의 뿌리 노드를 삭제하는 과정은 다음과 같다. 시간 복잡도는 $O(log n)$이다.

  1. 뿌리 노드를 삭제한다.
  2. 힙의 가장 깊은 곳의 맨 우측에 있는 노드를 찾아 뿌리 노드로 옮긴다. 배열로 구현한 경우 배열의 맨 끝에 있는 요소를 배열의 맨 앞으로 옮기면 된다.
  3. 옮겨온 노드를 양쪽 자식 노드보다 크거나 작은지 비교한다.
  4. 옮겨온 노드가 제 위치에 있다면 연산을 종료한다. 그렇지 않으면 자식 노드 중 가장 크거나(최대 힙) 작은(최소 힙) 노드와 자리를 바꾸고 3번으로 돌아가 반복한다.

• 힙 구현에 사용되는 배열의 0번 인덱스를 사용하지 않고 1번 부터 사용하는 경우의 인덱스 계산법은 다음과 같다.

  • 왼쪽 자식 노드의 인덱스 = 부모 노드의 인덱스 * 2
  • 오른쪽 자식 노드의 인덱스 = 부모 노드의 인덱스 * 2 + 1
  • 자식 노드의 인덱스 / 2 = 부모 노드의 인덱스

• 0번 인덱스를 사용할 경우엔 다음과 같다.

  • 왼쪽 자식 노드의 인덱스 = 부모 노드의 인덱스 * 2 + 1
  • 오른쪽 자식 노드의 인덱스 = 부모 노드의 인덱스 * 2 + 2
  • (자식 노드의 인덱스 - 1) / 2 = 부모 노드의 인덱스

• 뿌리 노드 교체는 뿌리 노드를 삭제하면서 새로운 노드를 삽입하는 연산이다. 삭제 후 삽입하는 연산과 결과는 같지만 힙의 특성상 두 연산을 한번에 진행하면 연산과정을 한번만 수행하면 되기 때문에 따로 하는 것보다 더 효율적이다.

힙의 종류

• 이진 힙(binary heap)
• 이항 힙(binomial heap)
• 2-3 힙(2-3 heap)
• K-D 힙(K-D heap)
• 피보나치 힙(Fibonacci heap)

힙의 활용

• 우선순위 큐(Priority Queue) 구현
• 힙 정렬(Heapsort) 구현
• 프림 알고리즘(Prim's algorithm)
• 데이크스트라 알고리즘(Dijkstra's algorithm)
• 허프만 코딩(Huffman coding)

프로그래밍 언어 별 힙의 사용

C++

• C++ 표준 라이브러리의 <algorithm> 헤더에서 힙을 위한 기능을 제공한다.
• 힙을 위한 자료형이나 컨테이너 클래스가 따로 있는건 아니며 주어진 컨테이너의 모든 요소를 힙 속성을 만족하는 순서로 변환하는 방식이다.
• 변환을 완료하면 컨테이너의 모든 요소들이 힙 속성을 만족하는 순서로 재배치된다.
• 힙을 위한 컨테이너로는 보통 std::vector를 사용한다.
• 주어진 컨테이너를 힙 구조로 변환하기 위해 std::make_heap()을 사용한다. 비교 방법을 지정하지 않으면 기본적으로 최대 힙이 되며 최소 힙으로 만들 수도 있다.
• 힙의 push와 pop 연산을 위한 std::push_heap(), std::pop_heap()이 있다.

파이썬

• C++와 마찬가지로 힙을 위한 빌트인 자료형이나 클래스는 없지만 주어진 리스트를 힙 구조로 변환할 수 있다.
• 힙 구현을 위한 내장 모듈인 heapq가 있다. 이 모듈을 사용하려면 import 해야한다.
• 이 모듈에서 최소 힙은 모든 연산이 구현되어있지만 최대 힙은 일부 연산만 구현되어있다.
• heapq.heapify(list)을 사용하면 리스트의 모든 요소가 최소 힙 배열의 순서대로 재구성된다.
• 최소 힙의 push와 pop 연산을 위한 heapq.heappush(heap, item)와 heapq.heappop(heap) 함수를 제공한다.
• heapq.heappushpop(heap, item) 함수는 힙에 item을 push한 다음, 가장 작은 요소를 pop하고 반환한다. 이 함수는 heappush()를 호출하고 heappop()를 호출하는 것보다 더 효율적이다.
• heapq.heapreplace(heap, item) 함수는 위와 반대로 가장 작은 요소를 pop하고 반환한 후에 item을 push하는 함수이다. 이 함수도 heappop()한 다음 heappush()하는 것보다 더 효율적이다.
• heapq._heapify_max(list) 함수는 리스트를 최대 힙으로 변환해준다.
• 최대 힙의 pop연산을 위한 heapq._heappop_max(heap) 함수가 있지만 최대 힙의 push연산을 위한 함수는 없다.
• 숫자 데이터만 다룰 경우, heappush할때 삽입할 값을 음수로 변환하여 삽입하고, heappop으로 추출된 값을 다시 음수로 변환하여 원래 값이 나오게 만들면 최소 힙을 마치 최대 힙 같이 활용할 수 있다.

참고자료

• 이것이 자료구조+알고리즘이다
• 위키백과 힙
• 위키백과 이진 힙
• https://en.cppreference.com/w/cpp/algorithm/make_heap
• https://docs.python.org/ko/3/library/heapq.html