트리(Tree) 개념정리

개발자 강세영·2023년 9월 30일

선택 트리 스레드 이진 트리 스레드 트리 알고리즘 이진 트리 자료구조 토너먼트 트리 트리 트리 순회 트리 용어

TIL

목록 보기

59/70

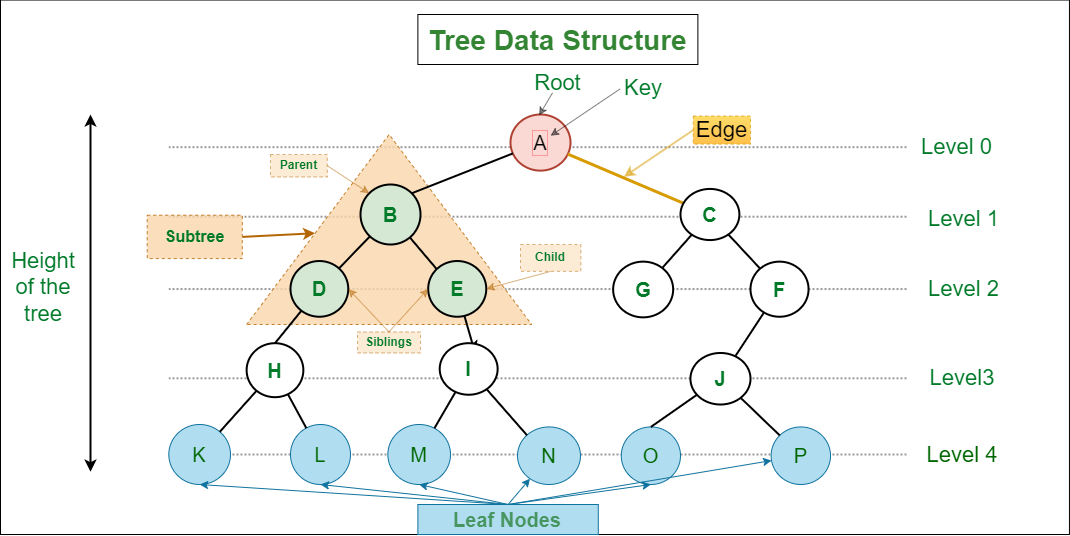
트리(Tree) ADT

트리는 일련의 연결된 노드로 계층적 구조를 나타내는 추상적 자료형이다. 나무를 닮았다고 하여 트리라고 부른다.
나무의 뿌리에서 가지가 나오고 가지 끝에는 잎이 달린 모습을 떠올리면 된다.
회사의 조직도, 여러 게임에서 나오는 스킬트리 등이 바로 트리다.
트리 구조는 컴퓨터 과학 분야에서 활용도가 높다. 운영체제의 파일 시스템, HTML을 다루는 DOM(Document Object Model), 검색 엔진, 데이터베이스 등 트리 기반으로 구현된 것이 많다.
트리는 연결 리스트처럼 연결된 노드로 구성되고 넓게는 그래프(자료구조)에 포함된다. 그래프와 마찬가지로 노드(정점)와 간선으로 이루어져 있는 계층적 데이터의 집합이다.
트리는 그래프와는 다르게 노드들 사이에 부모-자식 관계가 있다.
트리의 방향은 항상 단방향이고 부모 노드에서 자식 노드 방향으로 간선이 연결된다.
자식 노드에서 부모 노드 또는 형제 노드 방향으로 연결되는 간선이 있다면 트리가 아니다.
연결된 자식 노드의 개수가 아예 없을 수도 있고 여러개 있을 수도 있다.
현실의 나무는 밑에 있는 뿌리의 위쪽으로 가지와 잎이 자라나지만, 트리 자료구조는 보통 거꾸로 자라는 나무처럼 표현한다.

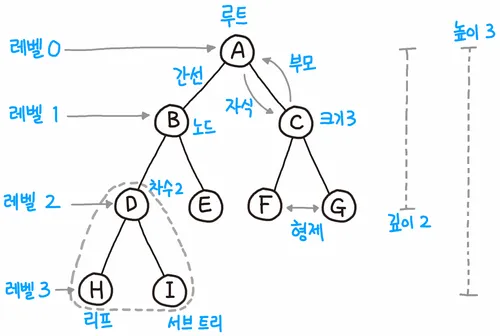
트리의 구성요소

노드(node): 트리를 구성하는 기본 원소이다. 정점(vertex)이라고도 한다.
간선(edge, line, link, arc): 노드들을 연결하는 선.
트리에서 간선의 개수는 노드의 개수 - 1 과 같다. 또한 이 명제의 역도 성립한다.
뿌리(root, 루트) 노드: 트리의 맨 위에 있고 부모 노드가 없는 노드.
잎(leaf, 리프) 노드: 트리의 맨 끝에 있는 노드. 맨 끝에 있으므로 자식 노드가 없다. 단말(terminal) 노드라고도 한다.
내부(internal 또는 inner) 노드: 뿌리와 잎 사이에 있는 모든 노드. 가지(branch) 노드라고도 한다.
비단말(non-terminal) 노드: 잎 노드와는 반대로 자식이 있는 노드.
뿌리, 가지, 잎 등은 모두 노드이며 노드의 위치에 따라 불리는 이름이 달라질 뿐이다. 만약 어떤 트리에 뿌리 노드 하나만 있다면 그 노드는 뿌리 노드와 잎 노드의 특성을 모두 가진 노드가 된다.

트리 관련 용어 정리

부모(parent), 자식(children) 노드: 트리는 계층적 자료구조이기 때문에 모든 노드들은 서로 부모 자식 관계가 있다. 트리의 한 노드에서 뿌리 노드 쪽으로 인접한 노드는 부모 노드가 되고 그 반대 방향으로 인접한 노드는 자식 노드가 된다. 뿌리 노드를 제외한 모든 노드는 정확히 하나의 부모 노드를 가진다.
형제(sibling) 노드: 같은 부모 노드를 가지는 자식 노드들이다. 보통 왼쪽부터 순서대로 표현한다.
경로(path): 한 노드에서 다른 한 노드까지 이르는 길 사이에 있는 노드들의 순서를 경로라고 한다. 위의 그림에서 예를 들면 H노드에서 E까지의 경로는 H, D, B, E가 된다.
경로의 길이(length): 경로의 출발 노드에서 목적지 노드까지 거쳐야 하는 노드의 개수.
노드의 깊이(depth): 뿌리 노드에서 특정 노드까지의 경로의 길이. 위의 그림에서 예를 들면 H노드의 깊이는 3, B노드의 깊이는 1이 된다. 뿌리 노드의 깊이는 0이다.
레벨(level): 트리에서 깊이가 같은 노드들의 집합. 위 그림에서 레벨 2는 D, E, F, G가 된다.
트리의 높이(height): 뿌리 노드에서 가장 깊은 곳에 있는 잎 노드까지의 경로의 길이.
노드의 차수(degree): 특정 노드와 자식 관계인 노드의 개수. 트리는 일방향이므로 그래프 관점에서 보면 노드의 진출 차수를 의미한다. 트리에서 노드의 진입차수는 항상 0 또는 1이므로 대개 고려하지 않는다.
트리의 차수: 트리 내에 있는 노드의 차수 중에서의 최대값.
크기(size): 트리를 구성하는 노드의 개수.
너비(width): 특정 레벨의 크기 또는 트리에서 가장 많은 노드를 갖고 있는 레벨의 크기를 의미한다.
여러 개의 서로 독립적인 트리로 이루어진 집합은 숲(forest, 포레스트)이라고 한다.
하나의 노드로만 구성된 트리는 사소한 트리(trivial tree)라 하고, 노드가 전혀 없는 트리는 공백 트리(empty tree)라 한다.
서브트리(하위 트리, subtree): 서브트리는 트리를 구성하고 있는 작은 트리이다. 뿌리 노드를 제외한 모든 노드는 어떤 하위 트리의 뿌리 노드로 볼 수 있다. 한 하위 트리 역시 그 내부의 여러 개의 하위 트리로 구성되므로, 트리는 재귀적인(recursive) 구조를 갖는다.
루트 트리(rooted tree): 전체 트리의 유일한 루트 노드를 포함하는 트리이다. 보통 트리를 재귀적으로 정의할 때 필요한 개념이다. 특별한 언급이 없는 경우 그냥 트리라고 하면 루트 트리를 의미한다.
방향 트리(directed tree): 트리를 그래프의 일종으로 설명하기 위해 정의하는 개념으로, 트리의 간선이 방향성을 가진 트리이다. 앞서 설명했듯이 트리는 방향 그래프의 일종이기 때문에 모든 트리는 방향 트리이다.
트리 관련 용어들은 표준화가 덜 돼있어서 여러 문헌에서 그 의미가 미묘하게 다를 수 있다.
높이, 깊이, 레벨은 보통 0에서 시작하는 값으로 정의되지만 어떤 문헌에서는 1에서 시작하는 값으로 정의되기도 한다.

트리의 표현 방법

그래프 표현: 가장 일반적인 표현 방법으로, 그래프와 같은 모양으로 트리를 표현하는 방법이다. 트리는 단방향이므로 간선의 화살표는 생략할 수 있다.
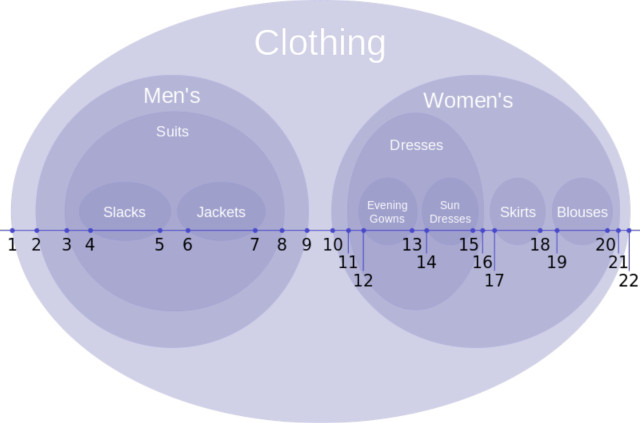
중첩된 괄호(nested parenthesis) 표현: 같은 레벨의 노드들을 괄호로 함께 묶어서 표현하는 방법이다. 가독성은 떨어지지만 트리를 하나의 수식처럼 표현할 수 있다. 위의 그림에 대해서는 다음과 같이 표현할 수 있다. (A(B(D(H)(I))(E))(C(F)(G)))
중첩된 집합(nested set) 표현: 트리를 다음과 같이 벤 다이어그램으로 나타내는 방법이다.
들여쓰기(indentation) 표현: 윈도우 탐색기의 폴더 트리나 리눅스의 tree 명령어 같이 들여쓰기로 트리를 표현하는 방법이다.

노드의 표현 방법

부모, 자식, 형제 노드의 연결을 표현하는 것으로 다음 두 가지의 방법이 있다.
N-링크 표현: 노드의 차수가 N이라면 노드가 N개의 링크를 갖고 있는데, 이 링크들이 각각 자식 노드를 가리키도록 노드를 구성하는 방법이다. 이 방법은 자식의 개수를 최대 N개로 고정하기 때문에 노드마다 차수가 다른 트리에는 적용하기 힘들다는 단점이 있다.
왼쪽 자식-오른쪽 형제(left child-right sibling, LCRS) 표현: 왼쪽 자식과 오른쪽 형제에 대한 포인터만을 갖도록 노드를 구성하는 방법이다. 이 방법은 N개의 차수를 가진 노드를 2개의 포인터만으로도 단순하게 표현할 수 있어 구현이 쉽다.

트리의 종류

트리는 자식 노드의 개수에 따라 분류하면 다음과 같다.
이진 트리(Binary Tree): 자식 노드를 2개까지 가질 수 있는 트리.
- 이진 탐색 트리(Binary Search Tree)
- 스레드 이진 트리(Threaded Binary Tree)
- 이진 힙(Binary Heap)
- 토너먼트 트리 또는 선택 트리(Selection Tree)
삼원 트리(Ternary Tree): 자식 노드를 3개까지 가질 수 있는 트리.
- 삼원 탐색 트리
- 삼원 힙
m-원 트리(m-ary, n-ary, k-ary, k-way 등은 모두 같은 의미): 자식 노드를 최대 m개 까지 가질 수 있는 트리. 이진 트리는 m=2, 삼원 트리는 m=3인 m-원 트리라고 볼 수 있다.
- 트라이(Trie): retrieval이라는 단어에서 따온 이름이다.
- m-원 탐색 트리

탐색 트리(Search Tree)

데이터 집합 내에서 특정 키를 찾기 위해 사용되는 트리이다.
탐색 트리 또한 이진 트리, 삼원 트리, m-원 트리로 구분할 수 있다. 대표적인 종류는 다음과 같다.
- 이진 탐색 트리(Binary Search Tree)
- 스플레이 트리(Splay Tree)
- AVL 트리(Adelson-Velsky-Landis Tree)
- 레드-블랙(Red-Black) 트리
- 2-3 트리, 2-3-4 트리
- AA 트리
- B-트리, B+ 트리, B* 트리, B*+ 트리, Bx 트리
- k-d 트리, K-D-B-트리, R-트리

이진 트리(Binary Tree)

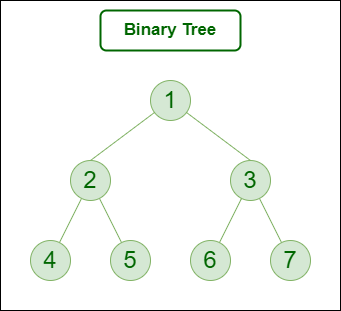
이진 트리는 하나의 노드가 자식 노드를 2개까지만 가질 수 있는 트리이다.
이진 트리는 속성에 따라 다음과 같이 구분할 수 있다.
정 이진 트리(full binary tree): 모든 노드의 자식이 0개 또는 2개인 이진 트리이다.
포화 이진 트리(perfect binary tree): 모든 단말 노드의 높이가 같고, 단말 노드가 아닌 노드는 모두 2개의 자식을 갖는 트리이다.
- 이진 트리에서 트리의 높이가 0부터 증가하는 값인 $n$ 이라고 할 때 이진 트리가 가질 수 있는 노드의 개수는 최대 $2^{n+1}-1$ 개이며, 포화 이진 트리는 이 개수를 모두 채운 이진 트리이다.
- 노드의 개수가 n개인 이진 트리 중에서 포화 이진 트리는 유일하게 하나만 존재한다.
- 모든 포화 이진 트리는 정 이진 트리이다.
완전 이진 트리(complete binary tree): 단말 노드들의 레벨 외에는 모두 차 있고 단말 노드들은 왼쪽부터 차있는 트리이다.
- 단말 노드가 왼쪽-오른쪽 순서대로 차 있지 않고 중간에 비어있는 부분이 있다면 완전 이진 트리가 아니다. 포화 이진 트리처럼 가득찬 모습이어야 하는 건 아니고 단말 노드의 순서만 충촉하면 완전 이진 트리가 된다.
- 완전 이진 트리는 항상 노드의 개수가 같은 트리 중 최소 높이를 갖는다.
  n개의 노드를 갖는 이진 트리의 최소 높이 $H_{min}$ 는 다음과 같다. $H_{min} = \lfloor log_2n \rfloor$
- 포화 이진 트리는 완전 이진 트리의 부분집합이다.
- 포화 이진 트리가 아닌 완전 이진 트리는 정 이진 트리일 수도 있고 아닐 수도 있다.
높이 균형(height balanced) 이진 트리: 뿌리 노드 기준으로 왼쪽 하위 트리와 오른쪽 하위 트리의 높이 차이가 1이하인 이진 트리이다.
완전 높이 균형(completely height balanced) 이진 트리: 뿌리 노드 기준으로 왼쪽 하위 트리와 오른쪽 하위 트리의 높이가 같은 이진 트리이다.
이진 트리를 이용한 탐색은 트리의 노드를 가능한 한 완전한 모습으로 유지해야 높은 성능을 낼 수 있기 때문에 이러한 관련 개념들을 알아두는게 중요하다.
앞서 언급했듯이 이진 트리에 관련된 용어도 문헌마다 명칭이나 의미가 조금씩 다를 수 있다.
수학자 외젠 카탈랑이 증명한 카탈랑 수에 의하면 노드가 n개인 서로 다른 이진 트리의 개수는 다음과 같다. ${\frac {(2n)!}{n!(n+1)!}}$

트리 순회(Tree traversal)

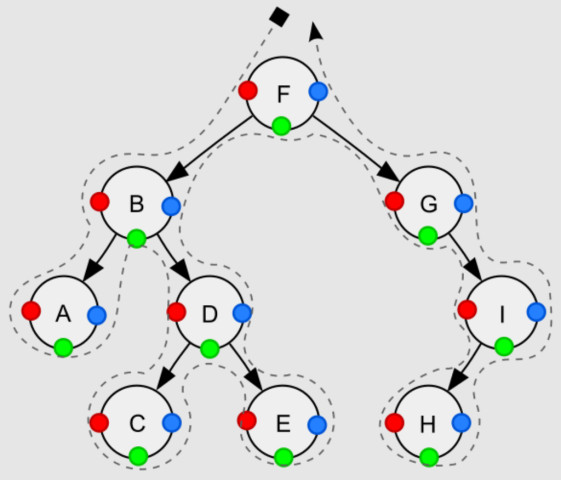
트리 순회는 트리의 모든 노드를 정확히 한 번만, 체계적인 방법으로 방문하는 과정이다. 이는 노드를 방문하는 순서에 따라 구분한다.
트리를 탐색하는 방법은 크게 깊이 우선 탐색(Depth First Search, DFS)과 너비 우선 탐색(Breadth First Search, BFS)으로 구분한다.
다음 목록은 DFS에 의한 트리 순회 방법이다. 여기서 설명하는 알고리즘들은 이진 트리에 대해서 작성되었지만, 다른 모든 트리에서도 일반화될 수 있다.
전위 순회(pre-order, NLR): 현재 노드 방문->왼쪽 하위 트리->오른쪽 하위 트리 순으로 순회하는 방법이다. 중첩된 괄호 표현법과 관련이 있다. 위의 그림에선 F, B, A, D, C, E, G, I, H 순서로 순회한다
중위 순회(in-order, LNR): 왼쪽 하위 트리->현재 노드 방문->오른쪽 하위 트리 순으로 순회하는 방법이다. 수식 트리와 관련이 있다. 위의 그림에선 A, B, C, D, E, F, G, H, I 순서로 순회한다.
후위 순회(post-order, LRN): 왼쪽 하위 트리->오른쪽 하위 트리->현재 노드 방문 순으로 순회하는 방법이다. 후위 표기식과 관련이 있다. 위의 그림에선 A, C, E, D, B, H, I, G, F 순서로 순회한다.
역 전위 순회(reverse pre-order, NRL): 전위 순회의 반대 방향으로, 현재 노드 방문->오른쪽 하위 트리->왼쪽 하위 트리 순으로 순회한다.
역 중위 순회(reverse in-order, RNL): 중위 순회의 반대 방향으로, 오른쪽 하위 트리->현재 노드 방문->왼쪽 하위 트리 순으로 순회한다.
역 후위 순회(reverse post-order, RLN): 후위 순회의 반대 방향으로, 오른쪽 하위 트리->왼쪽 하위 트리->현재 노드 방문 순으로 순회한다.
DFS에 의한 순회 방법들은 모두 재귀적으로(recursively) 구현할 수 있다.
레벨 순회(level-order): DFS가 아닌 BFS에 의한 순회방법이다. 같은 레벨의 모든 노드를 순회하면 다음 레벨의 노드들을 순회하는 과정을 트리의 끝까지 반복한다. 보통 큐(Queue)를 이용하여 구현한다. 위의 그림에선 F, B, G, A, D, I, C, E, H 순서로 순회한다.
DFS나 BFS로 분류되지 않는 몬테 카를로 트리 탐색같은 트리 순회 알고리즘도 있다.
어떤 이진 트리에 대한 전위-중위 순회 방문 순서가 주어지면 트리 구조를 유일하게(한 개) 정할 수 있다.

스레드 이진 트리(Threaded Binary Tree)

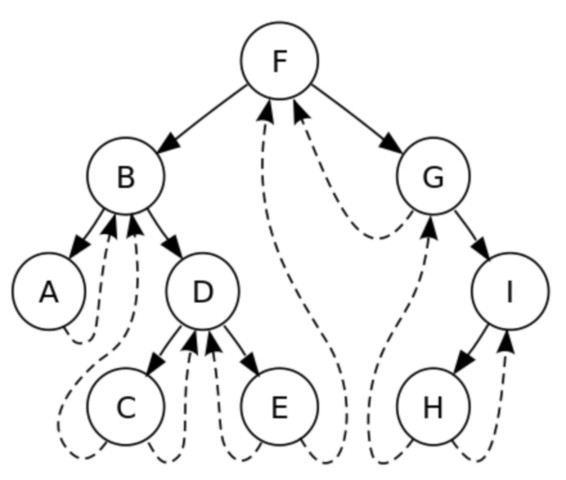
스레드 이진 트리(스레드 트리)는 스레드(thread)라는 포인터를 이용하여 트리를 특정한 순서로 순회하기 쉽도록 만든 이진 트리이다. 위 그림의 점선은 중위 순회(LNR) 순서대로 스레드 포인터가 가리키는 노드를 표현한 것이다.
이진 트리의 순회는 스택 같은 별도의 자료구조를 활용하거나 재귀적인 방법으로 구현할 수 있는데, 스레드 트리는 스레드 포인터로 순회 순서를 지정해주므로 일반적인 이진 트리보다 트리 순회를 더 편리하게 할 수 있다.
스레드는 오른쪽 스레드와 왼쪽 스레드 두 가지가 있다.
오른쪽 스레드는 정해진 순회 순서에 따른 특정 노드의 후속 노드를 가리키고 왼쪽 스레드는 특정 노드의 선행 노드를 가리킨다.
단일 스레드(single threaded) 트리는 각 노드의 스레드가 선행 노드 또는 후속 노드를 가리키고 이중 스레드(double threaded) 트리는 선행 노드와 후속 노드 모두를 가리킨다.
스레드 트리를 구현하는 방법은 다양하지만 대개 잎 노드의 남는 포인터를 다음에 방문할 노드를 가리키도록 만들고, 그 노드는 스레드가 있는 노드라는 걸 표현하는 스레드 플래그 변수를 활용하는 방식으로 구현한다.

토너먼트 트리(Tournament Tree) 또는 선택 트리(Selection Tree)

여러 개의 정렬된 데이터 리스트들을 완전한 순서를 유지하는 하나의 리스트로 통합하는 과정을 다방향 병합 알고리즘(k-way merge algorithm)이라고 한다. 병합 정렬의 과정 중 정렬을 완료한 하위 집합을 순서에 맞게 병합하는 과정이 바로 이 알고리즘이다.
토너먼트 트리는 다방향 병합 알고리즘을 위해 사용할 수 있는 특수한 트리이며 선택 트리(Selection Tree)라고도 부른다.
일반적으로 데이터 리스트가 k개 있으면 k-1번 비교해야 병합 정렬을 할 수 있지만, 토너먼트 트리를 사용하면 이 비교 횟수를 줄일 수 있다.
토너먼트 트리는 승자(winner) 트리와 패자(loser) 트리 두 종류가 있다.
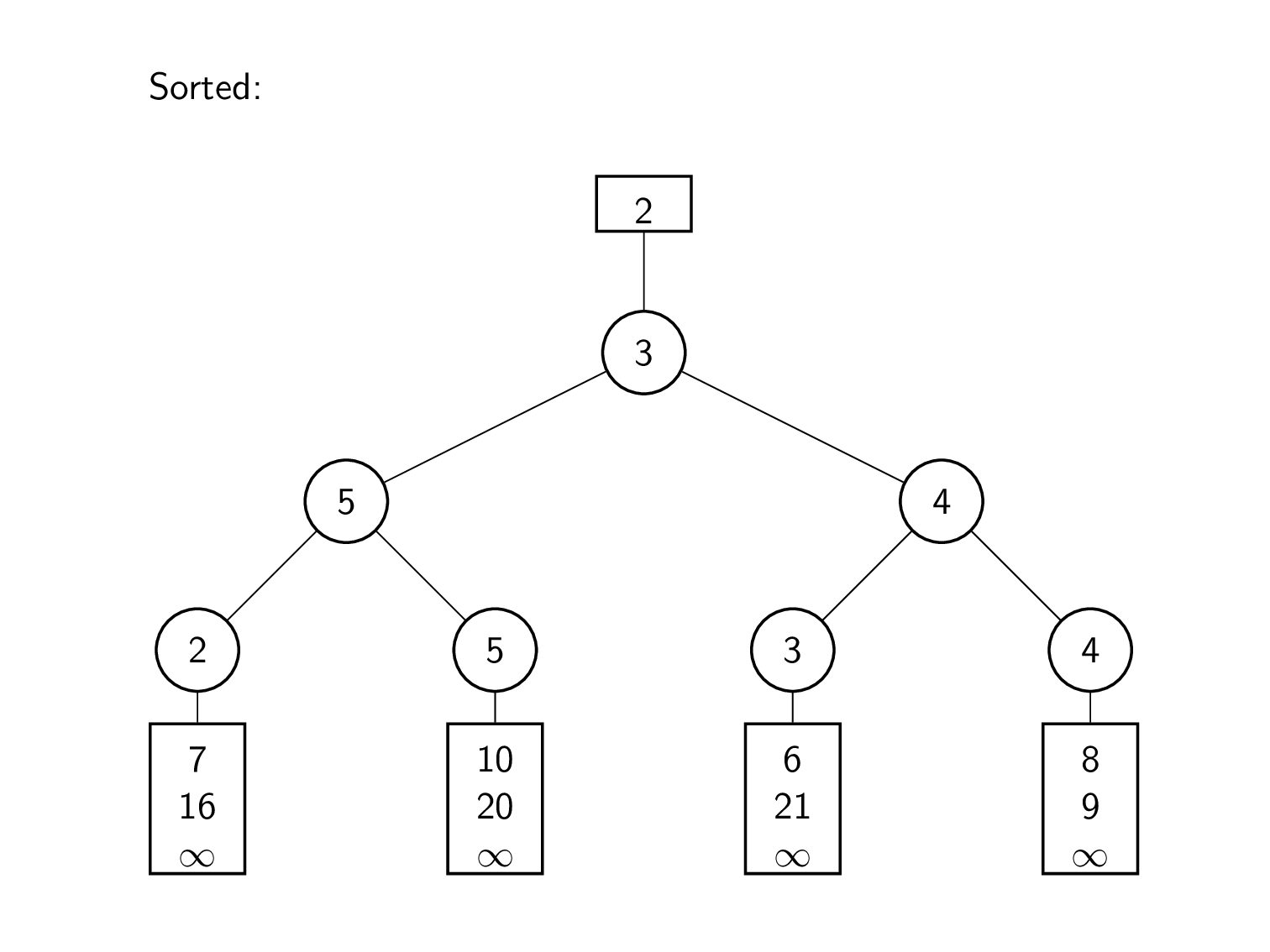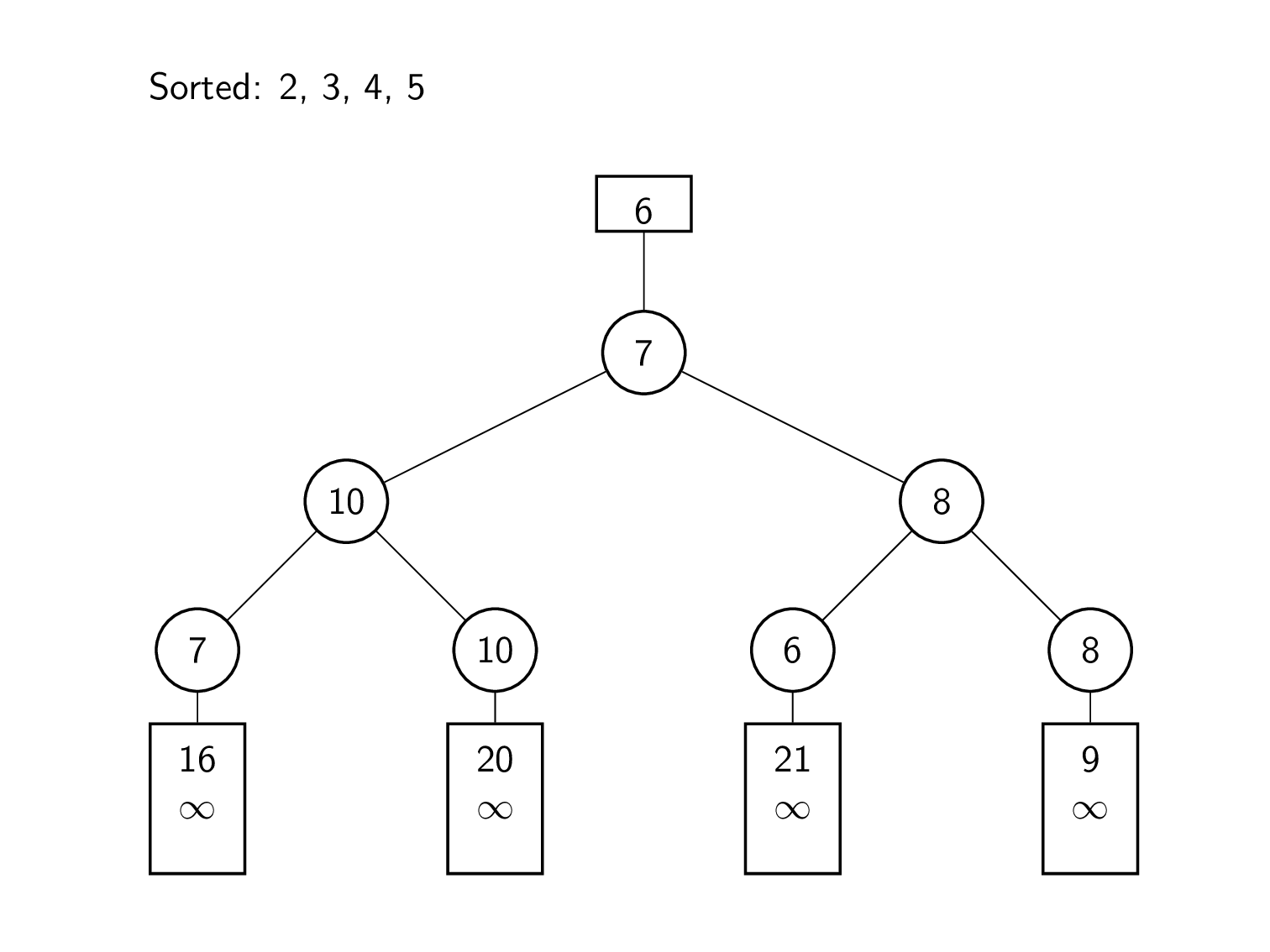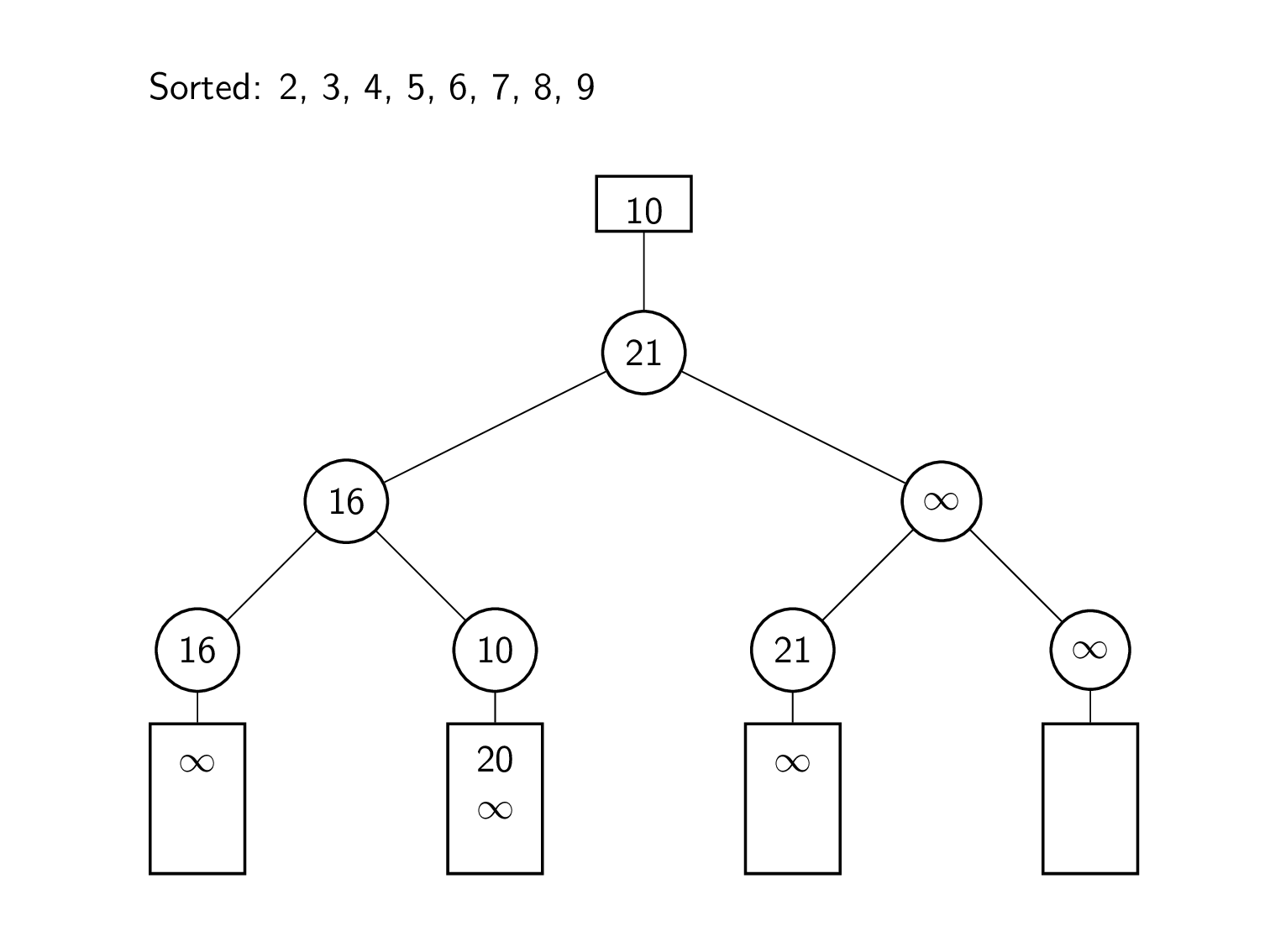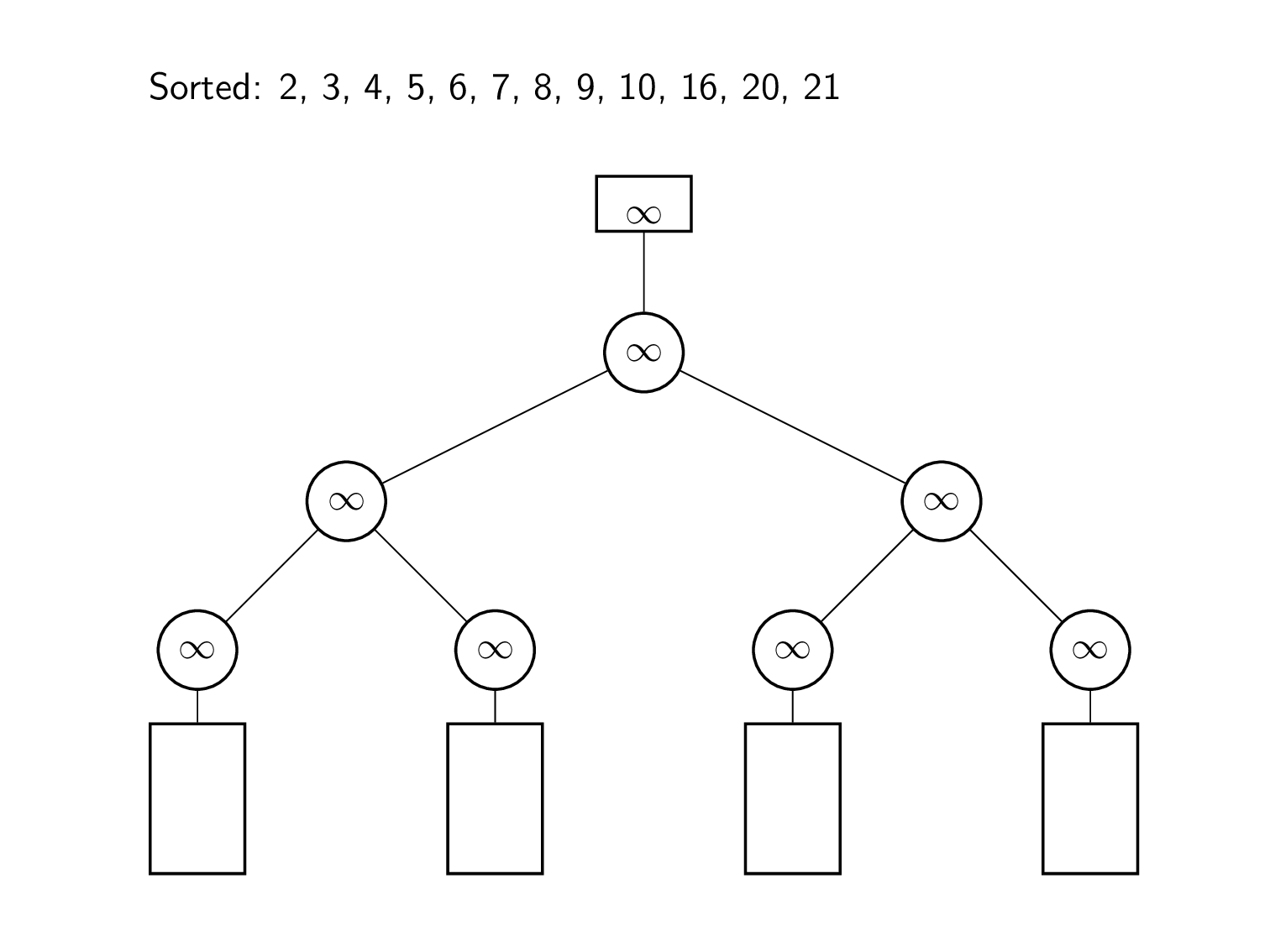
승자 트리는 각 노드가 두 자식 노드의 작은 값인 완전 이진 트리이다. 승자 트리를 만드는 과정은 다음과 같다.
1. 각 데이터 리스트의 최소값을 하나씩 잎 노드로 만든다.
2. 잎 노드를 2개씩 비교하여 그중 작은 값을 부모 노드로 만드는 과정을 반복하여 뿌리 노드까지 완성한다.
3. 뿌리 노드에 있는 값을 제거하고 그 값을 정렬된 결과를 저장하는 리스트에 삽입한다.
4. 최소값이 있던 데이터 리스트의 다음 요소를 잎 노드에 넣고 2번부터 다시 반복한다.
5. 더 이상 처리할 데이터가 없으면 연산을 종료하고 정렬된 리스트를 반환한다.
패자 트리는 각 노드가 두 자식 노드중 패자(큰 값)는 부모 노드에 저장하고 승자(작은 값)는 부모 노드의 부모 노드로 올라가서 다시 비교하는 방식으로 생성되는 트리이다. 승자 트리와 비슷하지만 뿌리 노드위에 최상위 0번 노드를 갖는다는 점이 다르다. 이 0번 노드에는 경쟁에서 이긴 최종 승자(최소값)가 저장된다.
패자 트리 알고리즘의 예시