분류(classification) 문제
분류 문제는 머신러닝의 대표적인 문제 유형 중 하나로, 주어진 데이터가 어떤 카테고리에 속하는지 예측하는 문제이다. 예를 들면 개와 고양이 사진을 분류하거나 음식 사진으로 음식의 종류를 예측하는 등의 문제가 바로 분류 문제이다. 분류 문제를 학습하려면 보통 정답(클래스 또는 레이블)이 있는 데이터가 필요하기 때문에 분류 문제를 위한 모델은 일반적으로 지도 학습 기법으로 학습한다. 이 글에서는 간단한 분류 예제를 통해 파이토치에서 분류 문제를 해결하는 방법을 정리하고자 한다.
예제 데이터 가져오기
간단한 분류 문제를 위한 데이터는 사이킷런 같은 머신러닝 라이브러리에서 제공하는 데이터셋 생성 기능을 활용하면 쉽게 만들 수 있다. 일단 사이킷런의 make_circles 함수로 학습 데이터를 생성해보자.
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
from torch import nn
import torch
import matplotlib.pyplot as plt
X, y = make_circles(n_samples=1000, noise=0.03, random_state=42)
plt.scatter(x=X[:, 0], y=X[:, 1], c=y, cmap=plt.cm.RdYlBu)
plt.show()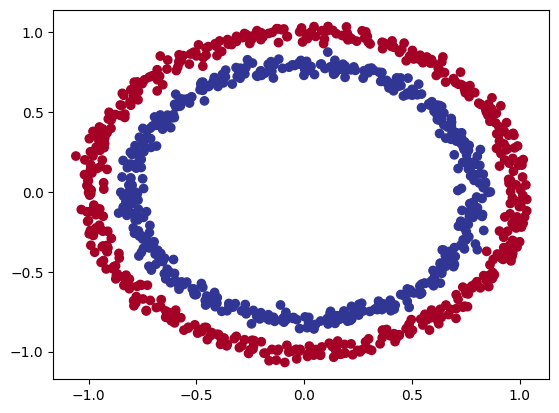
make_circles 함수는 위와 같이 큰 원과 작은 원 모양의 데이터를 생성한다. 매개변수로 생성할 샘플의 개수, 노이즈 값, 랜덤 시드값 등을 설정할 수 있다. 노이즈가 없으면 완전한 원 모양의 데이터가 되어 학습이 너무 쉽게 되므로 약간의 노이즈를 추가했다. 위의 코드를 실행해보면 위와 같은 원 모양의 데이터라는 것을 볼 수 있다. make_circles는 넘파이 배열인 X와 y를 반환하는데 여기서 y는 0 또는 1의 레이블 값을 가지므로 이 데이터를 분류하는 문제는 이진 분류 문제로 볼 수 있다.
선형 모델로 이진 분류 문제 풀어보기
분류 문제를 위한 손실함수와 옵티마이저
이런 간단한 이진 분류 문제에 대해서는 nn.BCEWithLogitsLoss 손실함수가 적합하다. nn.BCELoss도 있지만 이 함수는 이전 단계에서 시그모이드 함수를 통과해야만 사용할 수 있으므로 여기서는 BCEWithLogitsLoss를 사용한다.
이 함수는 이진 크로스 엔트로피 손실(Binary Cross-Entropy Loss)을 계산하고 시그모이드 활성화 함수를 적용하여 로짓(logit) 출력을 확률로 변환한다. 여기서 로짓이란 신경망에서 활성함수를 통과하기 전의 값들을 의미한다. 옵티마이저는 확률적 경사하강법(optim.SGD)를 사용하면 충분하다.
먼저 위의 학습 데이터에 대해 선형 레이어만으로 구성된 모델로 학습하고 테스트하는 코드는 다음과 같다.
# 학습 데이터를 텐서로 변환하고 분리
X = torch.from_numpy(X).type(torch.float)
y = torch.from_numpy(y).type(torch.float)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 선형 모델 정의
class CircleModelV1(nn.Module):
def __init__(self):
super().__init__()
self.layer_1 = nn.Linear(in_features=2, out_features=10)
self.layer_2 = nn.Linear(in_features=10, out_features=10)
self.layer_3 = nn.Linear(in_features=10, out_features=1)
def forward(self, x):
return self.layer_3(self.layer_2(self.layer_1(x)))
model_1 = CircleModelV1()
# 손실함수와 옵티마이저 정의
loss_fn = nn.BCEWithLogitsLoss()
optimizer = torch.optim.SGD(model_1.parameters(), lr=0.1)
# 정확도 계산 함수
def accuracy_fn(y_true, y_pred):
correct = torch.eq(y_true, y_pred).sum().item() # torch.eq는 요소의 일치 여부를 텐서로 반환함
acc = (correct / len(y_pred)) * 100
return acc
torch.manual_seed(42)
torch.cuda.manual_seed(42)
epochs = 1000
device = 'cuda' if torch.cuda.is_available() else 'cpu'
X_train, y_train = X_train.to(device), y_train.to(device)
X_test, y_test = X_test.to(device), y_test.to(device)
for epoch in range(1, epochs+1):
model_1.train()
y_logits = model_1(X_train).squeeze()
y_pred = torch.round(torch.sigmoid(y_logits)) # 정확도를 평가하기 위해 로짓 값에 시그모이드를 적용하고 torch.round()로 반올림
loss = loss_fn(y_logits, y_train)
acc = accuracy_fn(y_train, y_pred)
optimizer.zero_grad()
loss.backward()
optimizer.step()
model_1.eval()
with torch.inference_mode():
test_logits = model_1(X_test).squeeze()
test_pred = torch.round(torch.sigmoid(test_logits))
test_loss = loss_fn(test_logits, y_test)
test_acc = accuracy_fn(y_test, test_pred)
if epoch % 100 == 0:
print(f"Epoch: {epoch} | Loss: {loss:.5f} | Acc: {acc:.2f}% | Test loss: {test_loss:.5f} | Test acc: {test_acc:.2f}%")
위의 코드를 실행해보면 학습을 거듭해도 정확도와 손실값이 개선되지 않고 정체되는 것을 확인할 수 있다. 모델의 학습결과를 그래프로 시각화해보면 다음과 같다.
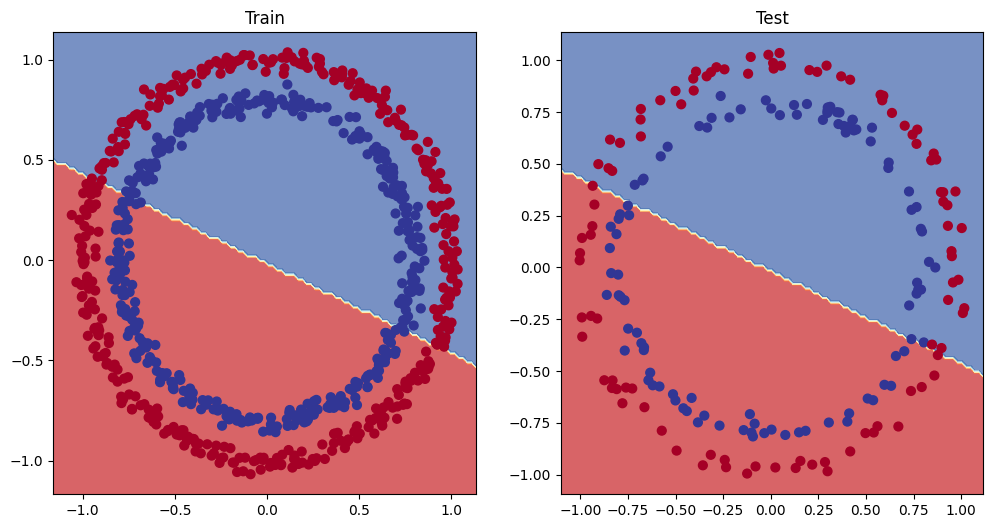
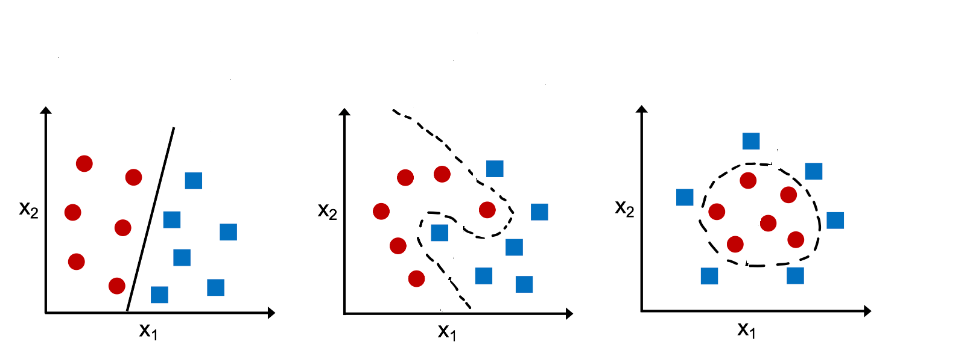
이러한 문제의 원인은 선형 레이어만을 사용하여 모델을 구성했기 때문이다. 이렇게 만들어진 모델의 결정경계는 선형적으로만 그려지므로 비선형적인 결정경계를 갖는 데이터를 제대로 학습할 수 없다. 비선형적 데이터를 학습하려면 RELU(rectified linear unit)같은 비선형 활성함수를 사용해야 한다. 비선형 활성함수는 신경망의 각 계층 사이에 비선형성을 도입하여 복잡한 패턴을 학습할 수 있게 해준다.
RELU는 현재 딥러닝에서 가장 널리 사용되는 활성함수 중 하나이며 많은 변형이 있다. RELU는 입력 값이 양수일 경우 그 값을 그대로 출력하고, 음수일 경우 0을 출력하는데, 이를 수식과 그래프로 나타내면 다음과 같다.
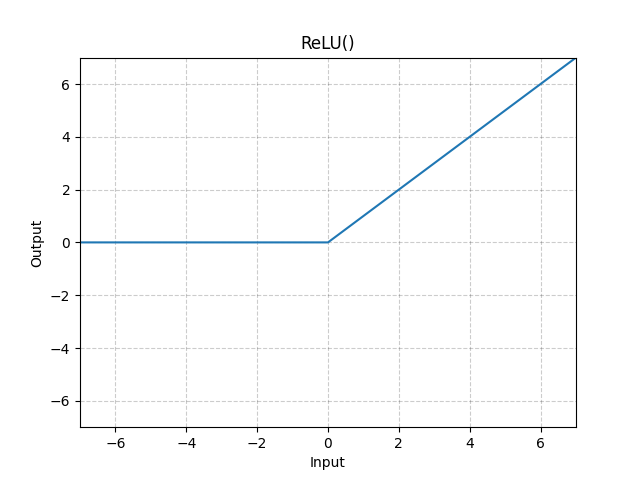
비선형적 데이터를 학습할 수 있도록 모델 수정
위의 모델에 RELU를 추가하고 학습하는 코드는 다음과 같다.
class CircleModelV2(nn.Module):
def __init__(self):
super().__init__()
self.layer_1 = nn.Linear(2, 10)
self.layer_2 = nn.Linear(10, 10)
self.layer_3 = nn.Linear(10, 1)
self.relu = nn.ReLU()
def forward(self, x):
# x = self.relu(self.layer_1(x))
# x = self.relu(self.layer_2(x))
# x = self.layer_3(x)
# return x
return self.layer_3(self.relu(self.layer_2(self.relu(self.layer_1(x)))))
model_2 = CircleModelV2().to(device)
loss_fn = nn.BCEWithLogitsLoss()
optimizer = torch.optim.SGD(params=model_2.parameters(), lr=0.1)
torch.manual_seed(42)
torch.cuda.manual_seed(42)
epochs = 2000
device = 'cuda' if torch.cuda.is_available() else 'cpu'
X_train, y_train = X_train.to(device), y_train.to(device)
X_test, y_test = X_test.to(device), y_test.to(device)
for epoch in range(1, epochs+1):
y_logits = model_2(X_train).squeeze()
y_pred = torch.round(torch.sigmoid(y_logits)) # logits -> prediction probabilities -> prediction labels
loss = loss_fn(y_logits, y_train) # BCEWithLogitsLoss calculates loss using logits
acc = accuracy_fn(y_true=y_train, y_pred=y_pred)
optimizer.zero_grad()
loss.backward()
optimizer.step()
model_2.eval()
with torch.inference_mode():
test_logits = model_2(X_test).squeeze()
test_pred = torch.round(torch.sigmoid(test_logits)) # logits -> prediction probabilities -> prediction labels
test_loss = loss_fn(test_logits, y_test)
test_acc = accuracy_fn(y_true=y_test, y_pred=test_pred)
if epoch % 100 == 0:
print(f"Epoch: {epoch} | Loss: {loss:.5f}, Accuracy: {acc:.2f}% | Test Loss: {test_loss:.5f}, Test Accuracy: {test_acc:.2f}%")코드를 실행해보면 모델의 성능이 대폭 개선된 것을 확인할 수 있다. RELU가 없는 모델1과 RELU를 추가한 모델2의 학습 결과를 시각화해보면 다음과 같다.
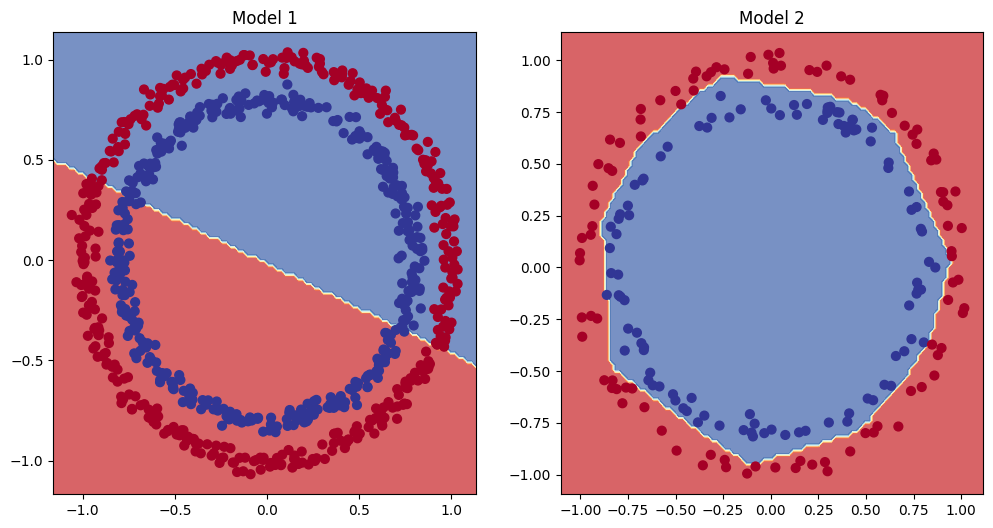
다중 분류 문제 풀어보기
위에서 이진 분류 문제를 학습한 방식을 그대로 다중 분류 문제에 대해 적용할 수 있다. 간단한 다중 분류 데이터는 사이킷런의 make_blobs 함수로 만들 수 있다. 이 함수는 여러 개의 중심점에 뭉쳐진 모양의 데이터를 생성한다. make_blobs 함수로 학습 데이터를 생성하는 코드는 다음과 같다.
from sklearn.datasets import make_blobs
NUM_CLASSES = 4
NUM_FEATURES = 2
RANDOM_SEED = 42
X_blob, y_blob = make_blobs(
n_samples=1000,
n_features=NUM_FEATURES, # X features
centers=NUM_CLASSES, # y labels
cluster_std=1.5,
random_state=RANDOM_SEED
)
X_blob = torch.from_numpy(X_blob).type(torch.float)
y_blob = torch.from_numpy(y_blob).type(torch.LongTensor)
X_blob_train, X_blob_test, y_blob_train, y_blob_test = train_test_split(
X_blob,
y_blob,
test_size=0.2,
random_state=RANDOM_SEED
)
plt.figure(figsize=(10, 7))
plt.scatter(X_blob[:, 0], X_blob[:, 1], c=y_blob, cmap=plt.cm.RdYlBu)
plt.show()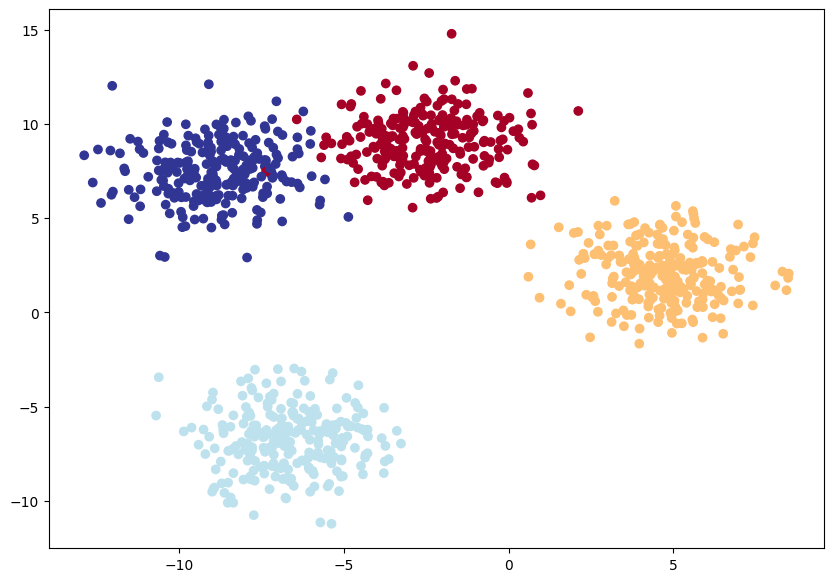
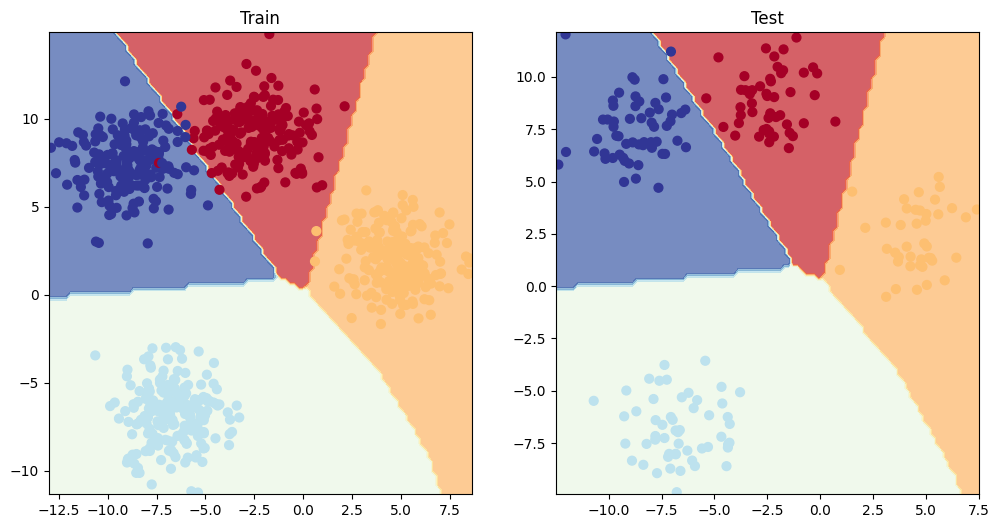
코드를 실행하면 위와 같이 4개의 중심점에 적당히 뭉쳐있는 모양의 데이터를 확인할 수 있다. 다중 분류를 위한 모델은 위에서 RELU를 추가한 모델과 비슷하게 정의하지만 손실함수는 다중 분류를 위해 크로스 엔트로피 함수를 사용해야 한다. 옵티마이저는 그대로 SGD를 사용한다. 또한 모델을 통과한 로짓 값들에 대해 소프트맥스(softmax) 함수를 적용하여 각 클래스에 속할 확률 값들을 얻는다. 이 확률값들에 대해 argmax함수를 적용하여 예측값들을 구하고 정확도를 계산하면 된다.
소프트맥스 함수는 argmax함수를 매끄럽게 만든 함수라는 의미로 소프트맥스라고 부르며 다중 클래스 분류 문제에서 자주 사용된다. 이 함수는 주어진 입력 벡터에서 각 요소의 값을 0~1의 확률 값으로 변환하며, 변환된 확률 값들의 합계는 항상 1이 된다. 이 함수를 수식으로 나타내면 다음과 같다.
소프트맥스를 활용하는 코드는 다음과 같다.
class BlobModel(nn.Module):
def __init__(self, input_features, output_features, hidden_units=8):
super().__init__()
self.linear_layer_stack = nn.Sequential(
nn.Linear(input_features, hidden_units),
nn.ReLU(),
nn.Linear(hidden_units, hidden_units),
nn.ReLU(),
nn.Linear(hidden_units, output_features)
)
def forward(self, x):
return self.linear_layer_stack(x)
device = 'cuda' if torch.cuda.is_available() else 'cpu'
blob_model = BlobModel(input_features=2, output_features=4, hidden_units=8).to(device)
loss_fn = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(blob_model.parameters(), lr=0.1)
torch.manual_seed(42)
torch.cuda.manual_seed(42)
epochs = 100
X_blob_train, y_blob_train = X_blob_train.to(device), y_blob_train.to(device)
X_blob_test, y_blob_test = X_blob_test.to(device), y_blob_test.to(device)
for epoch in range(1, epochs+1):
blob_model.train()
y_logits = blob_model(X_blob_train)
y_pred = torch.softmax(y_logits, dim=1).argmax(dim=1)
loss = loss_fn(y_logits, y_blob_train)
acc = accuracy_fn(y_blob_train, y_pred)
optimizer.zero_grad()
loss.backward()
optimizer.step()
blob_model.eval()
with torch.inference_mode():
test_logits = blob_model(X_blob_test)
test_pred = torch.softmax(test_logits, dim=1).argmax(dim=1)
test_loss = loss_fn(test_logits, y_blob_test)
test_acc = accuracy_fn(y_blob_test, test_pred)
if epoch % 10 == 0:
print(f"Epoch: {epoch} | Loss: {loss:.5f}, Acc: {acc:.2f}% | Test Loss: {test_loss:.5f}, Test Acc: {test_acc:.2f}%")위의 코드를 실행한 학습 결과를 시각화하면 다음과 같다.