문자열 알고리즘

개발자 강세영·2024년 4월 20일

KMP LZ77 RLE 데이터 압축 라빈-카프 문자열 문자열 검색 보이어 무어 알고리즘 양방향 문자열 검색 알고리즘 자료구조 허프만 코딩

TIL

목록 보기

66/70

문자열(string)의 의미와 유래

컴퓨터 과학에서 문자열이란 문자(character)를 나열한 것을 말한다.
string의 사전적 의미는 줄 또는 끈이다. 이 의미가 확장되어 여러 개의 문자로 구성되는 개념인 문자열을 뜻하는 단어가 되었다.
string은 19세기에 인쇄된 활자의 길이를 의미하는 용어로 쓰였다고 한다. 또한 수리 논리학, 이론 언어학 등의 분야에서 string을 유한한 순서로 나열된 기호라는 의미로 쓰기 시작하면서 현재의 의미가 굳어졌다.
문자열 처리를 위한 알고리즘이나 자료구조 등에 대해 연구하는 것을 문자열학(stringology)이라 부르기도 한다.

문자열 알고리즘의 종류

문자열 검색(searching 또는 matching) 알고리즘
데이터 압축(compression) 알고리즘
문자열 조작(manipulation) 알고리즘
문자열 정렬(sorting) 알고리즘
문자열 파싱(parsing) 알고리즘
정규 표현식 관련 알고리즘

문자열 검색 알고리즘

검색의 대상이 되는 비교적 긴 문자열을 텍스트(text) 또는 건초더미(haystack),
일치 여부를 판단하기 위한 비교적 짧은 문자열을 패턴(pattern) 또는 바늘(needle)이라고 한다.
문자열 검색 알고리즘은 텍스트에서 패턴과 일치하는 부분을 찾는 알고리즘이다.
대개 텍스트에서 패턴이 일치하는 첫번째 위치만 찾는 것이 아닌 모든 위치를 찾는다고 가정하고 구현한다.
문자열 검색 알고리즘은 접근 방식에 따라 패턴을 전처리하는 방법과 텍스트를 전처리하는 방법으로 구분할 수 있다.
텍스트가 자주 바뀌는 경우엔 패턴을 전처리하는 방법이 적합하다. 일반적으로 패턴이 텍스트보다 짧으므로 패턴을 전처리하여 공간 사용량을 절약하는 것이 좋기 때문이다.
텍스트가 고정적인 경우엔 텍스트를 전처리하는 방법이 적합하다. 일반적으로 텍스트는 큰 공간을 차지하지만 한 번만 전처리해 두면 다양한 패턴에 대해 효율적으로 검색을 수행할 수 있기 때문이다.
문자열을 구성하는 문자들의 유한 집합을 알파벳이라 하며 $Σ$ 기호로 표현한다. 이는 형식 언어 이론의 알파벳과 같다.
영어 대문자만으로 만든 문자열의 경우 알파벳은 $Σ=\{A,B,C,...,Z\}$ 이지만, DNA 서열의 알파벳은 $Σ=\{A,C,G,T\}$ 이며, 이진 데이터는 $Σ=\{0, 1\}$ 이다.

브루트 포스(brute force) 또는 우직한(naïve) 검색 알고리즘

전처리를 하지 않는 가장 간단한 문자열 검색 알고리즘이며 구현은 쉽지만 비효율적이다.
텍스트의 처음(0)부터 마지막 인덱스(n-m)까지 패턴과 일치하는 부분이 있는지 확인하는 방식이다.
텍스트의 길이를 $n$ , 패턴의 길이를 $m$ 이라 할 때 이 알고리즘의 평균적인 시간 복잡도는 $Θ(n+m)$ 이며, 최악의 경우 $O(nm)$ 이다.
텍스트의 마지막 부분까지 검색해야 패턴이 나오면 최악의 경우가 된다.
예를 들면 텍스트는 aaaaaaaabc인데 패턴이 abc인 경우이다.

유한 오토마타를 이용한 검색(Finite-state-automaton-based search)

결정적 유한 오토마타(deterministic finite-state automata, DFA)를 이용하여 문자열을 검색하는 방법이다. 여기서 말하는 오토마타는 수학적인 모델로, 일정한 규칙에 따라 상태가 변하는 추상적인 기계를 말한다.
유한 오토마타는 유한한 상태들의 집합과 그 상태들 간의 전이(transition)를 기반으로 동작하는 오토마타이다. 주어진 입력에 따라 상태가 바뀌며, 최종적으로 수용 상태(accepting state)에 도달하는지를 판별하는 기계라고 할 수 있다. 유한 오토마타는 유한한 개수의 상태만 가지며, 미리 정의된 규칙에 따라 상태를 전이한다.
DFA는 다음과 같이 5-튜플로 구성된다.
$M=(I,Q,f,F,\sigma)$
$I$ : 입력기호의 유한집합(알파벳의 유한집합)
$Q$ : 상태의 유한집합
$f$ : 상태 전이 함수 ( $Q\times I \rightarrow Q$ )
$F$ : 수락 상태(목표 상태)들의 집합 ( $F\subseteq Q$ )
$\sigma$ : 초기 상태 ( $\sigma \in Q$ )
이 알고리즘은 텍스트의 처음부터 끝까지 한 글자씩 상태를 전이시켜서 목표상태에 도착하면 패턴을 찾은 것으로 처리하는 방식이다.
상태 전이 함수는 상태표로 나타낼 수 있고, 상태표는 상태 그래프(상태도)로 나타낼 수 있다. 상태표를 만드는 과정이 이 알고리즘의 전처리 작업이라 할 수 있다.
$n$ 은 텍스트의 길이, $m$ 은 상태 집합의 크기, $|Σ|$ 는 알파벳의 크기라고 할 때
상태 전이 함수의 상태표를 가장 효율적으로 만들 경우 $Θ(|Σ|m)$ 만큼의 시간이 필요하며 텍스트를 한 글자씩 확인하므로 이 알고리즘의 시간 복잡도는 $Θ(n+|Σ|m)$ 이 된다.
패턴에 포함된 문자들만으로 상태표를 만들고 나머지 문자들은 하나로 처리하면 상태표의 크기를 줄일 수 있어 수행시간을 개선할 수 있다. 또한 추가적인 알파벳 인덱스 변환 테이블을 생성하여 활용한다.
이렇게 하면 새롭게 만든 상태표( $|Σ'|m$ )에 알파벳 인덱스 변환 테이블(알파벳의 크기와 동일)을 사용하므로 시간 복잡도는 $Θ(|Σ'|m+|Σ|)$ 이 된다. 이 방식은 KMP 알고리즘과 비슷하지만 KMP의 전처리 방식이 더 간명하고 효율적이다.
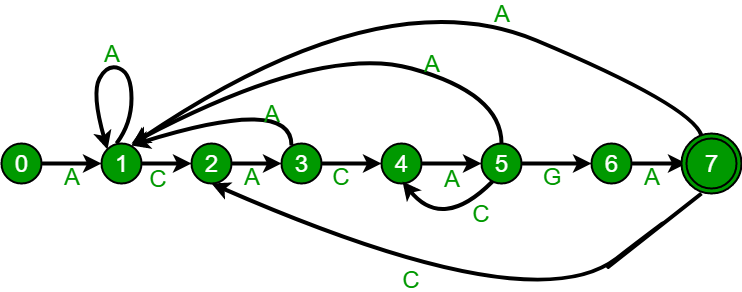
다음은 알파벳이 {A, C, G, T}일 때, ACACAGA라는 패턴으로 만든 상태도와 상태표 예시이다.

라빈-카프(Rabin-Karp) 알고리즘

마이클 라빈과 리처드 카프가 개발한 문자열 검색 알고리즘이다.
텍스트의 처음부터 끝까지 패턴의 길이 만큼 서브스트링(부분 문자열)을 추출하여 해시 값을 계산하고, 이 값이 패턴의 해시 값과 같으면 서브스트링과 패턴이 일치하는지 검사하는 방식으로 진행한다.
서로 다른 문자열이 동일한 해시 값을 반환할 수 있으므로 패턴 일치 검사를 생략할 수는 없다.
이 알고리즘의 해시 함수는 문자열을 특정한 진법으로 변환하여 숫자로 바꾸는 함수이다.
해시 함수에서 사용하는 진법은 알파벳의 크기에 따라 결정한다. 예를 들어 영어 소문자는 26진수, 아스키 코드는 128진수 이다.
문자열에 대해 숫자 변환까지만 할 수도 있고, 숫자 변환 후 나머지 연산까지 처리할 수도 있다.
나머지 연산을 하지 않으면 알파벳 또는 패턴의 크기에 따라 해시 값이 너무 커져서 오버플로우 문제가 발생할 수 있다.
나머지 연산을 하는 경우 해시 충돌을 최소화하기 위해 충분히 큰 소수를 선택해야 한다.
예를 들어 알파벳이 영어 소문자이고 패턴이 abcde라면 패턴의 해시 값은 다음과 같이 계산한다.
26진수 변환 : $0\cdot26^4+1\cdot26^3+2\cdot26^2+3\cdot26^1+4\cdot26^0 = 19010$
위의 결과값을 소수 101으로 나머지 연산 : $19010 \bmod 101 = 22$
패턴의 해시 값과 텍스트의 첫번째 서브스트링의 해시 값을 구하는 것이 이 알고리즘의 전처리 작업이 된다.
첫번째 서브스트링의 해시 값을 구해두면 두번째 서브스트링부터는 한 글자씩만 바뀌므로 이전 서브스트링의 해시 값을 이용하여 한 글자씩만 빼고 더해주는 방식으로 해시 값을 빠르게 계산할 수 있다. 나머지 연산의 비용이 크기 때문에 이러한 계산 테크닉을 활용하는게 좋다.
예를 들어 abcde의 다음 서브스트링이 bcdef라면 앞서 구한 abcde의 해시 값을 이용하여 다음과 같이 계산할 수 있다.
$(22\cdot26-0\cdot(26^5 \bmod 101)+5\cdot26^0) \bmod 101=72$
bcdef 다음이 cdefg라면 다음과 같다.
$(72\cdot26 - 1\cdot(26^5 \bmod 101) + 6) \bmod 101 = 21$
텍스트 전체를 검사하는데 $Θ(n)$ 의 시간이 걸리고, 일치 검사를 할 때 $Θ(m)$ 시간이 걸리며 일치 횟수를 $k$ 라고 할 때, 라빈-카프 알고리즘의 패턴 검사 시간 복잡도는 $Θ(n+km)$ 이 된다.
하지만 패턴이 자주 발견되는 특이한 경우가 아니라면 $k$ 는 상수 시간 즉, $k=O(1)$ 으로 볼 수 있다. 따라서 평균적인 패턴 검사 시간 복잡도는 $Θ(n)$ 이다. 모든 자리에서 패턴이 일치하면 최악의 경우가 되어 $k=n-m+1$ 이 되므로 최악의 패턴 검사 시간 복잡도는 $O(n+(n-m+1)m)=O(nm)$ 이 된다.
전처리 과정의 시간 복잡도는 $O(m)$ 이며 이를 패턴 검사 시간에 더하면 알고리즘의 전체적인 시간 복잡도가 된다.
이 알고리즘의 공간 복잡도는 $O(1)$ 이다.

KMP(Knuth-Morris-Pratt) 알고리즘

도널드 커누스, 제임스 모리스, 본 프랫이 공동 개발한 문자열 검색 알고리즘이다. 이름의 첫 글자를 따서 KMP 알고리즘이라고 한다.
이 알고리즘의 핵심 아이디어는 이전에 일치한 부분을 재사용하여 검색 시간을 줄이는 것이다. 이를 위해 패턴을 전처리하여 매칭에 실패했을 때 돌아갈 위치를 저장하는 배열을 생성하고, 이 배열을 이용하여 텍스트를 검색한다.
전처리 배열을 구축하는 방법은 구현마다 조금씩 다를 수 있다.
초기화 값(-1 또는 0), 배열의 크기(패턴의 길이와 같게 또는 1 더 크게), 접두부와 접미부의 계산방법 등이 이에 해당된다.
초기화 값은 -1, 전처리 배열의 크기는 패턴의 길이와 같고, 접미부에서 불일치하면 초기화 값으로 돌아가는 방식으로 구현한 파이썬 코드는 다음과 같다.

# 패턴 전처리 함수
def prep_KMP(pat: str):
    m = len(pat)
    F = [0] * m
    F[0] = -1
    idx = -1

    for i in range(1, m):
        while idx >= 0 and pat[i] != pat[idx + 1]:
            idx = F[idx]
        if pat[i] == pat[idx + 1]:
            idx += 1
        F[i] = idx

    return F

# 패턴 검사 함수
def KMP(txt: str, pat: str):
    n = len(txt)
    m = len(pat)
    F = prep_KMP(pat)
    idx = -1
    matches = []

    for i in range(n):
        while idx >= 0 and txt[i] != pat[idx + 1]:
            idx = F[idx]
        if txt[i] == pat[idx + 1]:
            idx += 1
        if idx == m - 1:
            matches.append(i - m + 1)
            idx = F[idx]

    return matches

print(prep_KMP("aabaa"))  # [-1, 0, -1, 0, 1]
print(KMP("aabaabaaa", "aabaa"))  # [0, 3]

패턴의 길이가 $m$ 일 때, 전처리 작업의 시간 복잡도는 $Θ(m)$ 이다. 전처리 함수는 이중 루프로 구성되지만 안쪽 루프의 반복 횟수가 바깥 루프의 횟수보다 커질 수 없기 때문이다.
패턴 매칭 과정 또한 전처리와 비슷하게 루프가 구성되므로 텍스트의 길이가 $n$ 일 때 패턴 매칭의 시간 복잡도는 $Θ(n)$ 이다.
패턴의 길이가 텍스트의 길이보다 현저히 작다고 가정하면( $m<<n$ ) 전처리를 포함한 전체적인 시간 복잡도는 $Θ(n)$ 이며 공간 복잡도는 $Θ(m)$ 이다.

보이어-무어(Boyer–Moore) 알고리즘

로버트 보이어와 제이 스트로더 무어가 개발한 문자열 검색 알고리즘이다.
KMP 알고리즘과 비슷하게 패턴 내의 문자들의 관계를 이용하여 매칭 시 중복된 비교를 줄이며 패턴을 찾는 방법이다.
KMP 알고리즘은 패턴의 앞부분부터 시작하지만 이 알고리즘은 패턴의 뒷부분부터 시작한다는 점이 다르다.
문자를 비교하다 불일치가 발생하거나 매치를 찾으면 패턴을 오른쪽으로 이동시켜야 하는데 보이어-무어 알고리즘은 이를 위해 불일치 문자 규칙(bad-character rule)과 일치 접미부 규칙(good-suffix rule)이라는 두가지 방법을 사용한다. 또한 항상 두 방법 중 더 많이 이동시킬 수 있는 값을 선택하여 패턴을 이동시킨다.
불일치 문자 규칙은 문자별로 비교하다가 불일치가 발생하면 그때의 텍스트의 문자가 패턴에서 가장 마지막에 나타는 위치를 찾아서 불일치가 발생한 곳으로 패턴을 이동시키는 것이다. 패턴에 나타나지 않는 문자는 마지막 위치 정보를 -1로 둔다.
일치 접미부 규칙은 비교를 하다가 불일치가 발생하면 그 직전까지 일치된 서브스트링 정보를 활용하여 패턴을 이동시키는 것이다. KMP의 전처리 방식과 비슷하지만 패턴의 오른쪽 서브스트링에 대해 전처리한다는 점이 다르다.
패턴에 대해 불일치 문자 배열과 일치 접미부 배열을 만드는 작업이 이 알고리즘의 전처리 과정이 된다.
패턴의 길이가 $m$ 일 때, 전처리 과정의 시간 복잡도는 $\Theta(m)$ 이다.
텍스트의 길이가 $n$ 일 때, 최악의 경우엔 패턴을 이동시킬 때 마다 문자 비교가 일어나기 때문에 시간 복잡도는 $O(nm)$ 이 되며 공간 복잡도는 $Θ(k+m)$ 이다.
최선의 경우엔 텍스트의 위치가 패턴의 길이만큼씩 증가하고 문자가 항상 불일치하여 한 번의 문자 비교만 일어난다. 따라서 최선의 시간 복잡도는 $Ω(n/m)$ 이 된다.
불일치 문자 규칙만 사용하여 더 단순하게 수정된 알고리즘(Boyer–Moore–Horspool)이 있다.

양방향 문자열 검색 알고리즘(Two-way string-matching algorithm)

막심 크로슈모르와 도미니크 페린이 개발한 문자열 검색 알고리즘이다.
KMP와 보이어-무어처럼 패턴을 전처리하는 방식이며 두 알고리즘을 적절히 혼합한 알고리즘이다.
전처리 과정에서 패턴을 왼쪽 부분과 오른쪽 부분으로 분할하는데 이 분할 방법을 임계 인수분해(critical factorization)라고 한다.
패턴 전처리와 검색 모두 선형 시간에 가능하므로 시간 복잡도는 각각 $O(m)$ , $O(n)$ 이다.
공간 복잡도가 $O(log m)$ 으로 KMP와 보이어-무어보다 효율적이다.
이 알고리즘은 캐시 친화적이며 효율적으로 최적화된 서브루틴을 사용하여 성능이 좋다고 알려져있다. 또한 다양한 표준 라이브러리에서 사용되고 있다.

데이터 압축 알고리즘

데이터 압축(data compression, source coding, bit-rate reduction)이란 원본 데이터보다 적은 공간을 사용하여 데이터를 표현할 수 있도록 만드는 과정이다.
원본 데이터를 압축된 데이터로 변환하는 것을 인코딩(encoding), 압축된 데이터를 압축되기 전의 상태로 되돌리는 것을 디코딩(decoding)이라고 한다.
데이터 압축은 데이터의 복원 가능 여부에 따라 무손실 압축과 손실 압축으로 구분된다.
무손실(loseless) 압축은 압축된 데이터로부터 원본 데이터를 완벽하게 복원할 수 있는 방식으로, 데이터의 내용이 모두 중요한 경우 사용된다. 대표적인 알고리즘은 RLE, 허프만 코딩, LZ77 등이 있으며 데이터 포맷은 ZIP, FLAC, GIF 등이 있다.
손실(lossy) 압축은 무손실 압축의 반대 개념으로, 압축된 데이터로부터 원본 데이터를 완벽하게 복원할 수 없는 방식이다. 데이터의 내용이 약간 변형되더라도 크기를 줄이는 것이 더 중요한 경우에 사용된다. 대표적인 알고리즘은 이산 코사인 변환(Discrete Cosine Transform), 웨이블릿 변환(Wavelet Transform) 등이 있으며 데이터 포맷은 JPEG, MPEG, MP3, aptX 등이 있다.
일반적으로 영상이나 음성과 같은 데이터는 인간이 압축된 데이터와 원본 데이터 간의 차이를 인지하기 어려우므로 손실 압축이 유용하다. 그러나 텍스트 같은 데이터는 사소한 차이로도 인간의 인지적 변화가 크게 나타날 수 있기 때문에 손실 압축을 적용하기 어렵다.
데이터 압축이 반드시 문자열을 압축하는 것은 아니지만 대부분의 데이터는 문자열로 나타낼 수 있으므로 문자열을 압축하는 것으로 압축 알고리즘을 설명할 수 있다.

RLE(Run-length encoding)

가장 간단한 무손실 압축 알고리즘으로, 문자열에서 동일한 문자가 연속해서 나타나는 것(run)을 그 문자와 반복 횟수로 압축하는 방법이다.
예를 들어 aaaa라는 문자열은 문자 a가 4번 반복되므로 (a, 4), a4, 4a 같은 형식으로 인코딩한다.
RLE로 인코딩된 데이터가 (b, 5)이면 문자 b가 다섯번 반복된다는 의미이므로 bbbbb로 디코딩 한다.
문자열의 길이가 $n$ 일 때, 문자열의 처음부터 끝까지 한 글자씩 처리하므로 RLE의 인코딩과 디코딩의 시간 복잡도는 모두 $O(n)$ 으로 같다.
반복되는 문자가 많은 데이터를 압축할 경우 괜찮은 알고리즘이지만 반복되는 문자가 적으면 압축된 데이터가 원본 데이터보다도 커질 수 있다.

허프만 코딩(Huffman coding)

데이비드 허프만이 개발한 무손실 압축 알고리즘으로 문자의 빈도 정보를 이용하여 빈도수가 클수록 짧은 코드를 부여하여 압축하는 방식이다.
허프만 코딩의 인코딩 과정은 다음과 같다.
1. 주어진 문자열에서 각 문자의 출현 빈도수를 계산한다.
2. 1번에서 구한 빈도수를 이용하여 허프만 트리를 만들어 각 문자에 이진 코드를 부여한다.
3. 입력 문자열의 각 문자를 이진 코드로 변환하여 압축된 문자열을 생성한다.
"this is an example of a huffman tree"라는 문자열로 만든 허프만 트리의 예시:
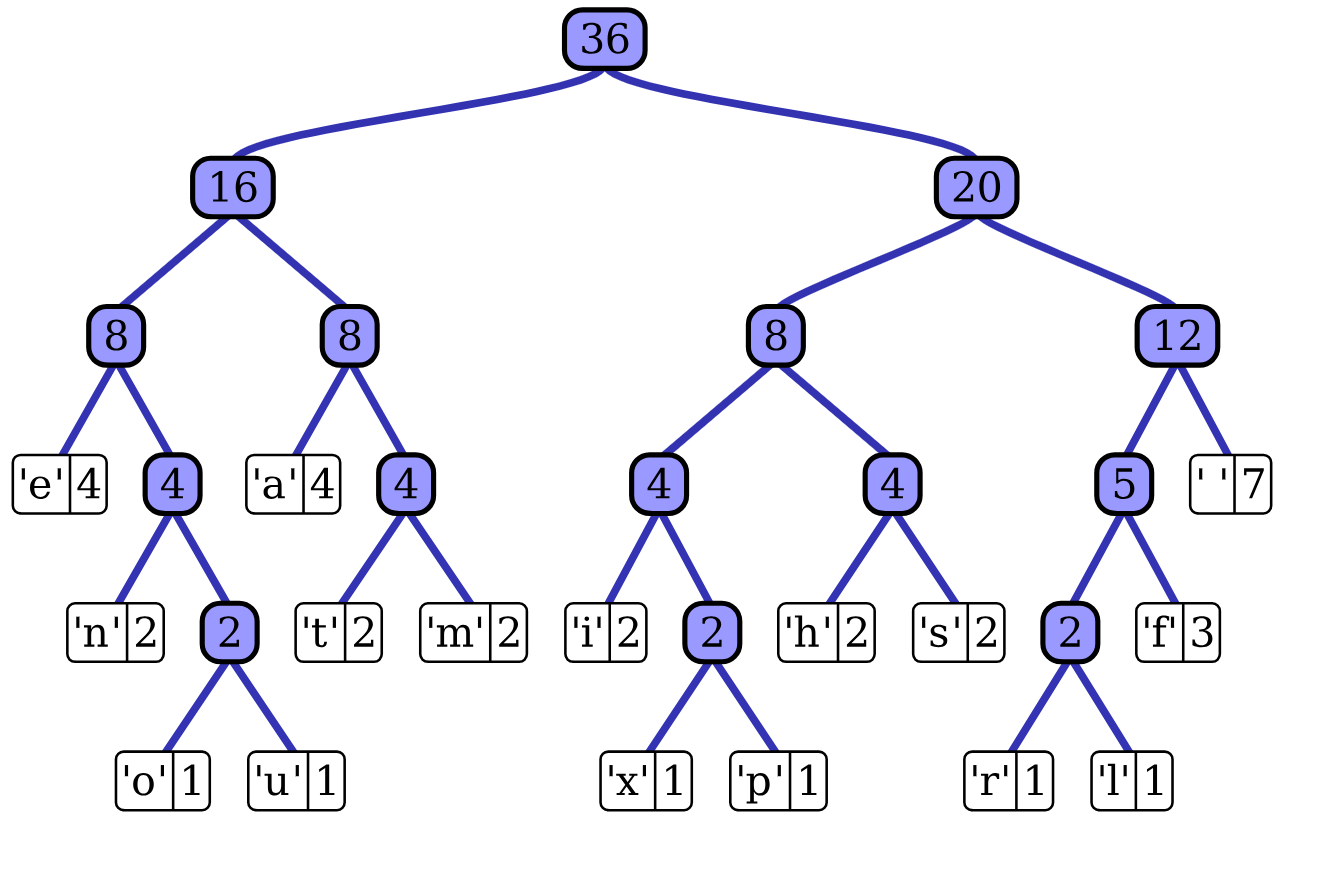
허프만 트리는 이진 트리의 일종으로, 모든 잎 노드는 각 문자를 표시하며 각 문자의 빈도수를 레이블로 가지는 트리이다.
허프만 트리에서 잎 노드를 제외한 모든 노드는 2개의 자식 노드를 가지며 두 자식 노드의 빈도수의 합을 레이블로 가진다.
허프만 트리의 생성은 그리디 알고리즘에 기반한 상향식으로 이루어지며 구체적인 과정은 다음과 같다.
1. 각 문자가 하나의 노드로 구성된 개별 트리를 만든다. 이 때 각 노드는 빈도수로 레이블한다.
2. 앞서 만든 트리 중에서 루트 노드의 레이블이 가장 작은 두 트리를 선택하여 하나의 트리로 만든다. 이 과정에서 최소 힙(min heap)을 활용할 수 있다.
- 트리를 합치는 방법: 두 트리의 루트 노드를 2개의 자식 노드로 갖도록 새로운 노드를 만들고 두 루트 노드와 연결한다. 이때 새로운 노드의 레이블은 자식 노드의 레이블의 합으로 표기한다. 또한 탐색을 위해서 자식 노드와 연결된 두 간선 중 왼쪽은 0, 오른쪽은 1로 레이블할 수 있는데, 이 작업은 생략할 수 있다.
1. 모든 트리가 하나로 합쳐질 때까지 2번을 반복한다.
허프만 코딩의 디코딩 과정은 다음과 같다.
1. 압축된 문자열을 1비트씩 읽으면서 허프만 트리의 루트 노드부터 탐색한다.
- 비트가 0이면 왼쪽 자식, 1이면 오른쪽 자식으로 이동한다.
1. 1번을 수행하다가 잎 노드에 도착하게 되면 그 노드에 해당하는 문자를 출력한다.
2. 압축된 문자열을 모두 처리할 때까지 1, 2번을 반복한다.
위의 허프만 트리 예시를 보면 공백(빈도수 7)은 111, 문자 a(빈도수 4)는 010, 문자 f(빈도수 3)는 1101, 문자 x(빈도수 1)는 10010이란 코드를 부여받았으며 빈도수가 클수록 짧은 코드를 부여받는 것을 확인할 수 있다.
인코딩된 문자열을 모호함 없이 디코딩하기 위해서는 코드 부여 방식이 접두부 코드여야 한다.
접두부 코드(prefix code)란 각 문자에 부여된 이진 코드가 다른 문자에 부여된 이진 코드의 접두부가 되지 않는 것으로, 인코딩된 문자열의 길이가 가장 짧은 최적의 코드가 된다. 예를 들어 문자 a에 부여된 코드가 101이라면 어떤 다른 문자도 1 또는 10 또는 101이 될 수 없다.
허프만 트리를 생성할 때 같은 빈도수의 노드가 여럿 존재하는 경우 노드를 합치는 순서에 따라 다른 형태의 허프만 트리가 될 수 있으며 그에 따라 이진 코드가 달라질 수 있다.
즉, 같은 문자열에 대해 서로 다른 허프만 트리가 생성될 수 있으므로 압축된 문자열의 내용도 달라질 수 있다. 단 동일한 원본 문자열에 대해 압축된 문자열의 내용이 다르더라도 압축된 문자열의 길이는 동일하다.
알파벳의 크기가 $|Σ|$ 일 때 허프만 트리 생성을 위한 초기 힙 구축에 $O(|Σ|)$ 이 걸리고, 힙에서 최소값을 삭제하는데 $O(log|Σ|)$ 의 시간이 걸리며 인코딩은 문자열의 길이 $n$ 에 비례하므로 전체 인코딩 과정의 시간 복잡도는 $O(|Σ|log|Σ|+n)$ 이다.
압축된 문자열의 길이가 $m$ 일 때 디코딩 과정의 시간 복잡도는 $O(|Σ|log|Σ|+m)$ 이다.

LZ77(Lempel and Ziv in 1977, LZ1), LZ78, LZW

LZ77은 아브라함 렘펠과 야콥 지프가 1977년에 발표한 무손실 압축 알고리즘이다.
LZ77은 허프만 코딩과 함께 ZIP 포맷을 위한 Deflate 압축 알고리즘의 기반이 되는 알고리즘이다.
이 알고리즘은 문자열에서 한 번 나왔던 문자열이 다시 나오는 경우 앞서 나온 위치와 반복된 부분의 길이를 이용하여 압축하는 방식이다.
예를 들어 abcdefgabcdehi라는 문자열을 보면 abcde라는 문자열이 두 번 반복되어 나온 것을 볼 수 있다. 두 번째 abcde는 7과 5라는 두개의 숫자로 표현할 수 있는데, 이는 현재 위치(g)의 7자리 앞에서 5개의 문자가 일치한다는 의미이다. 처음 등장하는 문자는 0 두 개로 표현한다.
abcdefgabcdehi를 인코딩 한 결과는 다음과 같다.
(0,0,a)(0,0,b)(0,0,c)(0,0,d)(0,0,e)(0,0,f)(0,0,g)(7,5,h)(0,0,i)
또한 이 알고리즘은 앞으로 나올 문자열과 지나간 문자열을 비교하기 위해 슬라이딩 윈도우(sliding window)라는 기법을 활용한다.
슬라이딩 윈도우는 컴퓨터 과학의 여러 분야에서 흔히 쓰이는 테크닉으로, 데이터의 일부분을 윈도우가 지나가면서 처리하는 방법이다. 예를 들어 abcde라는 문자열이 있고 윈도우의 크기가 3이라면 abc, bcd, cde의 차례대로 처리한다.
LZ77의 슬라이딩 윈도우는 앞으로 나올 문자 $L_s$ 개, 지나간 문자열 중 마지막 문자 $L_l$ 개를 보게 되며, 이때 일치하는 문자열이 여러개 존재하는 경우 가장 긴 것을 선택한다. 또한 일치하는 문자열의 최대 길이는 $L_s-1$ 이 되는데, 이는 인코딩 시 일치 바로 다음에 나오는 문자를 하나 표시해야 하기 때문이다.
압축된 코드를 하나씩 보면서 (0,0,a) 같이 처음 나오는 문자들은 바로 출력하고, (7,5,h) 같은 코드를 만나면 해당되는 위치의 반복 문자열을 찾아 출력하는 방식으로 디코딩한다.

LZ78

LZ78는 렘펠과 지프가 1978에 발표한 무손실 압축 알고리즘으로 LZ2라고도 부른다. 이 알고리즘은 사전(dictionary) 기반으로 반복되는 패턴을 효과적으로 찾아 압축할 수 있는 알고리즘이다.
LZ78는 또한 구현이 비교적 간단하며 다양한 데이터 유형에 적용할 수 있고 확장성도 좋은 알고리즘이다.
LZ78의 압축 과정은 다음과 같다.
1. 압축을 위한 빈 사전을 만든다.
2. 입력 데이터의 첫 번째 기호(문자)부터 시작하여 사전에 해당 기호의 존재 여부를 확인한다.
사전에 없는 새로운 패턴(기호의 조합)을 발견하면, 그 패턴을 사전에 추가하고 사전에서 그 패턴을 참조하는 인덱스와 다음 기호를 출력한다. 사전에 이미 존재하는 패턴인 경우, 패턴을 확장하여 새로운 패턴을 찾는다.
3. 새로운 패턴을 발견할 때마다, 이 패턴의 직전까지의 패턴에 해당하는 사전 인덱스와 새롭게 추가된 기호를 출력한다. 이후, 그 새로운 패턴을 사전에 추가한다.
4. 모든 입력 데이터가 처리될 때까지 이 과정을 반복한다.
예를 들어, 입력 데이터가 "ABABABA"라고 할 때 LZ78의 압축 과정은 다음과 같다.
1. A는 사전에 없으므로, 사전에 A를 추가하고 (0, A)를 출력한다.
2. B도 사전에 없으므로, 사전에 B를 추가하고 (0, B)를 출력한다.
3. A는 이미 사전에 있으므로, 다음 기호 B와 결합하여 AB를 확인한다. AB는 사전에 없으므로 (1, B)를 출력하고, AB를 사전에 추가한다.
4. A는 사전에 있으므로, AB를 확인하고, ABA를 만든다. ABA는 사전에 없으므로 (3, A)를 출력하고, ABA를 사전에 추가한다. 이런 식으로 입력 데이터가 모두 처리될 때까지 반복한다.

LZW(Lempel-Ziv-Welch)

LZW 압축 알고리즘은 LZ78 알고리즘의 개선된 버전으로, 1984년에 테리 웰치(Terry Welch)가 발표한 압축 알고리즘이다.
LZW는 압축 과정에서 일치하는 부분을 찾을 수 없을 때, 현재 입력 스트림 문자가 사전에서 기존 문자열의 첫 번째 문자로 가정되기 때문에(사전이 모든 가능한 문자로 초기화되었기 때문에) 마지막 일치 인덱스만 출력되는 방식으로 압축 효율을 개선하였다.
LZW는 GIF와 같은 다양한 포맷에서 사용되고 있다.

참고자료

개발자 강세영

이전 포스트

그래프 심화 개념정리

다음 포스트

문자열 알고리즘

TIL

문자열(string)의 의미와 유래

문자열 알고리즘의 종류

문자열 검색 알고리즘

브루트 포스(brute force) 또는 우직한(naïve) 검색 알고리즘

유한 오토마타를 이용한 검색(Finite-state-automaton-based search)

라빈-카프(Rabin-Karp) 알고리즘

KMP(Knuth-Morris-Pratt) 알고리즘

보이어-무어(Boyer–Moore) 알고리즘

양방향 문자열 검색 알고리즘(Two-way string-matching algorithm)

데이터 압축 알고리즘

RLE(Run-length encoding)

허프만 코딩(Huffman coding)

LZ77(Lempel and Ziv in 1977, LZ1), LZ78, LZW

LZ78

LZW(Lempel-Ziv-Welch)

참고자료

그래프 심화 개념정리

인공지능, 머신러닝, 딥러닝 관련 개념정리

0개의 댓글