CS231A - Camera Models

deutan·2026년 1월 7일

Computer Vision cs231a

CS231A

목록 보기

1/2

Introduction

CS231A는 기하학과 3D vision에 대한 이해를 다루는 코스이다.

비디오 강의는 제공되지 않았으며 PDF 및 과제만 업로드 되어 있다.

Course Overview

참고 자료

CS231A 자료

CS231A 과제 구현 Github

3D Vision Course Note

Camera Models

Abstract

카메라는 컴퓨터 비전 분야에서 가장 필수적인 요소이다.

우리가 다양하게 활용할 수 있는 세상을 남길 수 있는 사진이라는 출력을 하는 기계로서 동작한다.

따라서 어떻게 카메라를 모델링 할 수 있을지에 대한 공부를 하는 것은 컴퓨터 비전의 시작이다.

Pinhole Cameras

Normal Pinhole model

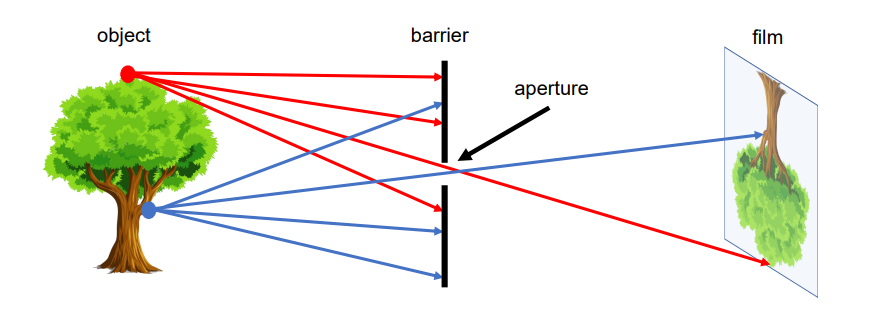
위 사진은 가장 간단하게 동작하는 카메라 모델인 Pinhole 모델이다.

3D Object의 각 지점에서 반사되는 빛은 무수히 많은 방향으로 반사된다.

만약 barrier가 존재하지 않는다면, film위의 모든 지점은 3D Object의 모든 지점으로 부터 반사된 많은 빛들에 의해 영향을 받아 제대로 된 상이 맺히지 않는다.

따라서 barrier를 통해 이 현상을 막고 작은 aperture를 통해 한개 또는 매우 적은 수의 광선많이 통과하여 film에 투영되도록 한다.

그리하여, 3D Object와 film 간의 일대일 매핑이 가능해진다.

이렇게 film에 투영된 것이 3D object의 image가 된다.

Formal Construction of pinhole model

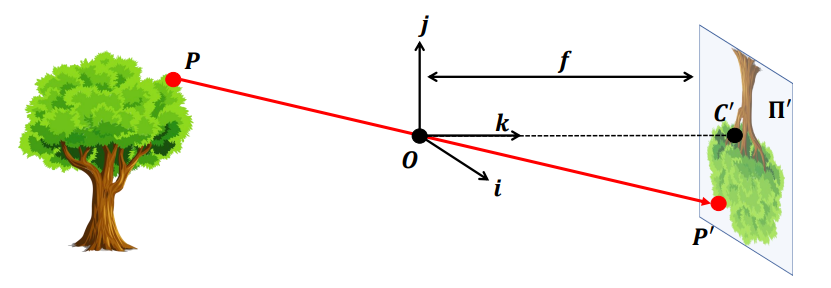
Formal construction of the pinhoe camera model은
Normal model을 수식으로 계산할 수 있도록 체계화 한 기하학/수학적 모델이다.

용어부터 살펴보면

film -> image or retinal plane
aperture -> pinhole: O or center of the camera
Distance between film and aperture -> focal length: f

가끔 image가 3D object와 O 사이에 생기는 것은 virtual image 또는 virtual retinal plane이라고 한다.

이때 image와 virtual image는 크기와 방향만 다르고 기학적으로는 완전히 동일하며 정보의 손실이 없는 똑같은 이미지이다.

그렇다면 우리는 어떻게 핀홀 모델을 사용할 수 있을까

P = $[x, y, z]^T$ 라는 3D Object 위의 한 점을 가정해보자.

P는 image plane 상에 P' = $[x', y']^T$ 으로 투영될 것이다.

또한 Pinhole O는 image plane에 C'으로 투영된다.

우리는 핀홀이 원점인 $[i, j, k]$ 동차좌표계 시스템을 정의할 수 있으며, k축에 대한 깊이 방향만 결정하면 이에 수직인 평면 이미지에서 가로와 세로방향을 결정하면 된다.

이때 k축은 O와 C'를 잇는 광학축(Optical axis)이라고 부른다.

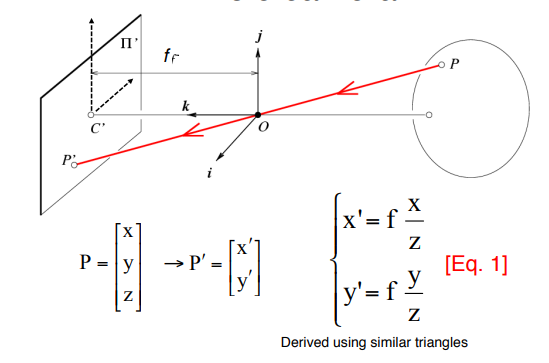
우리는 삼각형의 닮음비를 이용하여 P'을 $[f*(X/z), f*(Y/z)]$ 로 표현할 수 있다.

이때 z는 O와 물체사이의 거리이다.

여기까지의 가정은 aperture가 한 점이라는 것이었다.

하지만 실세계에서는 무한하게 작도록 만들 수 없으니 우리는 다양한 크기에서의 변화를 살펴볼 수 있다.

aperture의 사이즈가 커짐에 따라 더 많은 광선이 통과하기 때문에 이미지가 밝아지지만 선명도가 감소하는 블러 현상이 발생한다.

Modern Camera

Cameras and lenses

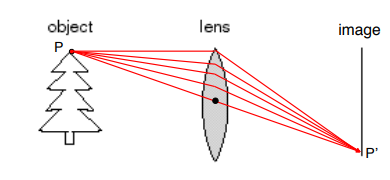
현대의 카메라는 이러한 선명도와 밝기의 trade-off를 해결하기 위해 렌즈 사용을 도입했다.

점 P에서 방출된 모든 빛이 렌즈를 통해 굴절되어 P'에서 융합된다.

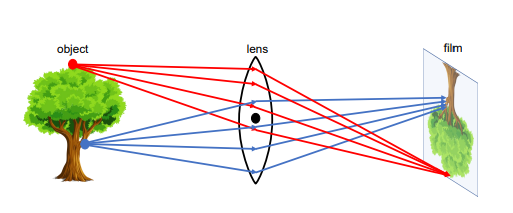
이런 심플한 렌즈 모델은 사방으로 퍼지는 광선을 한 점으로 정확히 모여 초점이 맞았다는 표현을 사용할 수 있지만,
특정 거리에 있는 물체에만 완벽히 작동하기 때문에 다른 거리에 있는 점에 대해서는 흐린 물체로 보인다.

이러한 렌즈의 특성때문에 P보다 멀거나 가까운 점 Q에 대해서는 정환학 물체를 담아낼 수 없기 때문에 컴퓨터 그래픽스나 사진학 같은 곳의 개념에서는 depth of field 라는 컨셉으로 알려져 있으며 선명한 사진을 담기 위한 효과적인 거리 범위이다.

Paraxial refraction model

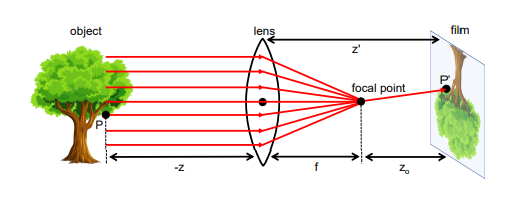
이 모델은 렌즈의 복잡한 특성을 중심은 직진하고 광학축과 평행하게 들어오는 빛은 초점으로 모인다는 두가지 규칙으로 단순화 하여, 핀홀 모델과 유사하게 투영공식을 적용하면서도 초점과 film사이의 거리 $z_0$ 을 이용해 $z'= f+z_0$ 정의한다.

이 모델은 실제 물리적 현상을 단순화하여 가정하기 때문에 오차가 발생한다.

렌즈를 아주 얇고 모든 빛이 광학축에 가까운 각도로 들어온다고 가정하지만, 실제 렌즈는 두께가 있으며 빛이 통과하는 렌즈의 부위마다 초점거리가 미세하게 다르기 때문에 방사 왜곡이 생긴다.

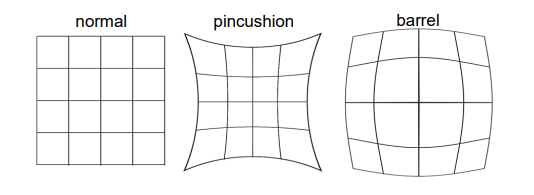
방사 왜곡(Radial Distortion)이란 렌즈의 결함이나 물리적 특성으로 인해 이미지의 배율이 광학축 중심에서의 거리에 따라 달라지는 현상이며, 이미지에서 멀어질수록 배율이 감소하는 Barrel Distortion과 멀어질수록 배율이 증가하는 Pincushion Distortion이 있다.

Digital Image Space

이 부분에서는 우리가 3D 공간에서 디지털 이미지로의 투영을 모델링할 때 자세히 다루어야 할 parameter에 대해 이야기하고자 한다.

앞에서 보았던 $R^3 -> R^2$ 투영을 Projective transformation이라고 부른다. 하지만 몇 가지의 이유로 인해 실제 디지털 이미지에서 우리가 보는 것과 직접적으로 일치하지는 않는다.

첫째, 디지털 이미지의 점들은 일반적으로 이미지 평면과 다른 기준 좌표계를 가진다.

둘째, 이미지 평면의 점들은 연속적이지만, 디지털 이미지는 이산적인 픽셀로 나뉜다

셋째, 실제 물리 센서는 매핑 과정에서 왜곡과 같은 비선형성을 유발할 수 있다.

Camera Matrix Model

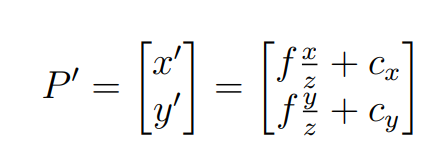
디지털 이미지의 시작 좌표는 통상적으로 왼쪽 하단 또는 상단이기 때문에 정중앙인 광학좌표계와 맞추기 위한
선형이동 offset인 $C_x$ , $C_y$ 가 필요하다.
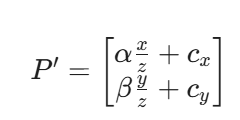
이미지 평면에서의 실제 cm, mm 등의 거리를 픽셀단위로 맞춰줘야 한다.
k와 l이 각각 x, y축의 이미지 픽셀 밀도로써 k = l이면 픽셀이 정사각형임을 의미한다.
또한 k와 l에 물리적 초점거리 f를 곱하여 픽셀단위의 초점거리를 만든다.

$\alpha = f \cdot k$
$\beta = f \cdot l$

이러한 변환들을 우리는 선형변환을 통해 빠르게 수행하고 싶지만, z로 나누는 연산은 선형변환이 아니기 떄문에 우리는 Homogeneous coordinate를 도입할 수 있다.

Homogeneous Coordinates

Homogeneous 좌표계는 임의의 상수 $w$ 에 대한 점 $P(x, y)$ 의 좌표를 $P(wx, wy, w)$ 로 표현하는 방식이다. ( $w != 0$ )
원래의 좌표를 구하려면 $w$ 를 1로 만들어 $P(x, y, 1)$ 로 만들면 된다.

컴퓨터 비전과 그래픽스의 분야에서는 이 좌표계를 사용하면서 많은 이점을 볼 수 있다.
참고 https://velog.io/@strongdeutan00/computer-vision-panorama

3D Object의 점을 이미지 평면상의 점과의 관계를 나타낼 때 3x4 행렬 $M$ 을 이용하여 나타낼 수 있으며

전체 투영행렬 $M$ 은 카메라의 내부 파라미터를 담고있는 카메라 행렬 $K$ 와 외부 구조 부분으로 분해할 수 있다.

여기서 카메라 행렬 $K$ 와 단위행렬에 0으로 이루어진 열벡터를 합친 외부 파라미터 행렬로 분해할 수 있다.

외부 파라미터 행렬은 가장 단순한 형태로 나타내져 있으며 복잡한 회전행렬과 이동벡터가 들어가 변형될 수 있다.

The complete Camera Matrix Model

전체 카메라 행렬 모델은 이전에 고려하지 않았던 요소 중 skewness를 추가한다.

카메라 좌표계의 두 축 $x,y$ 사이의 각도가 정확히 90도가 아닐 때 발생한다.

주로 센서 제조 과정에서의 미세한 오차로 인해 발생하며 현대의 카메라는 대부분 0에 가깝다.

비틀림 각도 $\theta$ 를 반영하여 정교화된 카메라 행렬 $K$ 는 위와 같다.

이 행렬에 포함된 값들을 내부 파라미터(Intrinsic Parameters)라고 부르며 위의 행렬은 총 5의 자유도를 가진다.

Extrinsic Parameters

이번에는 현실 세계에서의 좌표계의 점을 카메라 좌표계의 점으로 변환하는 과정이다.

회전행렬 $R$ 과 이동 벡터 $T$ 를 사용하며 카메라 기기 자체의 설계와는 무관하고, 카메라가 세계의 어디에 있으며 어느 방향을 보는지에 따라 결정된다.

위의 수식은 내부와 외부 파라미터를 결합하여 3D Object의 점을 2D 이미지 평면으로 투영하는 최종 수식이다.

전체 자유도는 11이며 내부 5, 외부 회전3, 외부 이동3 이다.

요약하자면 카메라는 자기 자신의 고유한 성질 5개와 외부에서의 위치 및 방향 정보 6개를 합쳐 11개의 변수를 통해 3차원 세상을 2차원으로 담아낸다.

Camera Calibration

우리는 단순히 카메라를 구입한다고 해서 정밀한 3D 연산을 바로 할 수는 없다.

미세한 오차를 가진 내부 변수와 어디에 설치했는 지에 따라 달라지는 외부 변수들 때문에
정확한 크기를 알고 있는 물체(Calibration Rig)를 카메라로 찍고 수학적으로 역추적하는
Calibration을 수행해야 한다.

투영 모델을 수립
최종 투영 식 $P' = K [R \mid T] P_w = MP_w$ 을 정의한다.
대응점 데이터 수집
좌표를 알고 있는 3D 점과 이미지에서 검출된 2D 점의 쌍을 수집한다.

각 대응점 쌍마다 2개의 방정식을 얻을 수 있기에 11개의 미지수를 구하기 위해서는
최소 6개 이상의 대응점 쌍이 필요하다.
선형 시스템 $Pm = 0$ 구성
이미지 좌표 $(u_i, v_i)$ 와 $3 \times 4$ 행렬 $M$ 의 각 행( $m_1, m_2, m_3$ ) 사이의 관계를 방정식으로 만든다.
$p_i = \begin{bmatrix} u_i \\ v_i \end{bmatrix} = MP_i = \begin{bmatrix} m_1 P_i / m_3 P_i \\ m_2 P_i / m_3 P_i \end{bmatrix}$
최적해 도출(SVD)
실측 데이터의 노이즈를 고려하여 오차를 최소화하는 해를 찾는다.

$\|\mathbf{P}m\|^2$ 을 최소화하면서 $\|m\|^2 = 1$ 이라는 조건을 만족하는 $m$ 을 찾는다.

$UDV^T$ 로 분해했을 때, $V$ 행렬의 마지막 열이 최적의 해 $m$ 이 된다.
이 $m$ 을 다시 3 x 4 형태의 행렬 $M$ 으로 재구성한다.

참고
https://velog.io/@strongdeutan00/%EA%B3%A0%EC%9C%A0%EA%B0%92-%EB%B6%84%ED%95%B4%EC%99%80-%ED%8A%B9%EC%9D%B4%EA%B0%92-%EB%B6%84%ED%95%B4
파라미터 분해

구해진 통합 행렬에서 개별 물리량을 추출한다.

스케일링 파라미터 $\rho$ : 행렬 $M$ 을 $1/\rho$ 로 나누어 정규화한다.
내부 파라미터 추출 : $\rho, c_x, c_y, \theta, \alpha, \beta$ 값을 차례대로 계산한다.
외부 파라미터 추출 : 회전 행렬 $R$ 의 각 행( $r_1, r_2, r_3$ )과 이동 벡터 $T$ 를 구한다.

주의사항: 만약 모든 대응점 $P_i$ 가 하나의 평면에 모여 있다면(Degenerate Configuration), 이 시스템은 풀리지 않으므로 반드시 입체적인 데이터 점들을 사용해야 한다.

Handling Distortion in Camera Calibration

실제 렌즈는 직선 투영이 아닌 방사 왜곡이 발생하기 때문에 왜곡을 반영하기 위해 기존 투영행렬 앞에 왜곡 계수 $\lambda$ 를 포함한 행렬 $Q$ 를 곱한다.

이는 식을 전개하면 파라미터들이 서로 곱해져서 일반적인 선형 방식으로는 풀 수 없는 비선형 최적화 문제가 된다.

이를 해결하기 위한 아이디어로 좌표의 비율은 왜곡의 영향을 받지 않고 유지된다는 점을 제시하였다.
$\frac{u_i}{v_i} = \frac{m_1 P_i}{m_2 P_i}$

위 식을 곱셈 형태로 정리하여 아래와 같은 선형 방정식을 나타내고
$v_i(m_1 P_i) - u_i(m_2 P_i) = 0$

모든 대응점에 대해 이 식을 세워 위에서 본 행렬-벡터 곱 형태로 만들어
SVD로 풀면 왜곡의 영향을 받지 않는 행렬 $M$ 의 1, 2 행을 정확히 찾아낼 수 있다.

따라서 남은 미지수인 3번째 행과 왜곡 계수는 훨씬 간단한 비선형 최적화 문제가 된다.

결론적으로는 복잡한 비선형 문제를 왜곡에 영향을 받지 않는 부분을 이용해 단순화된 비선형 문제로 만들어 해결한다.

deutan

Visual Computing and Learning

다음 포스트