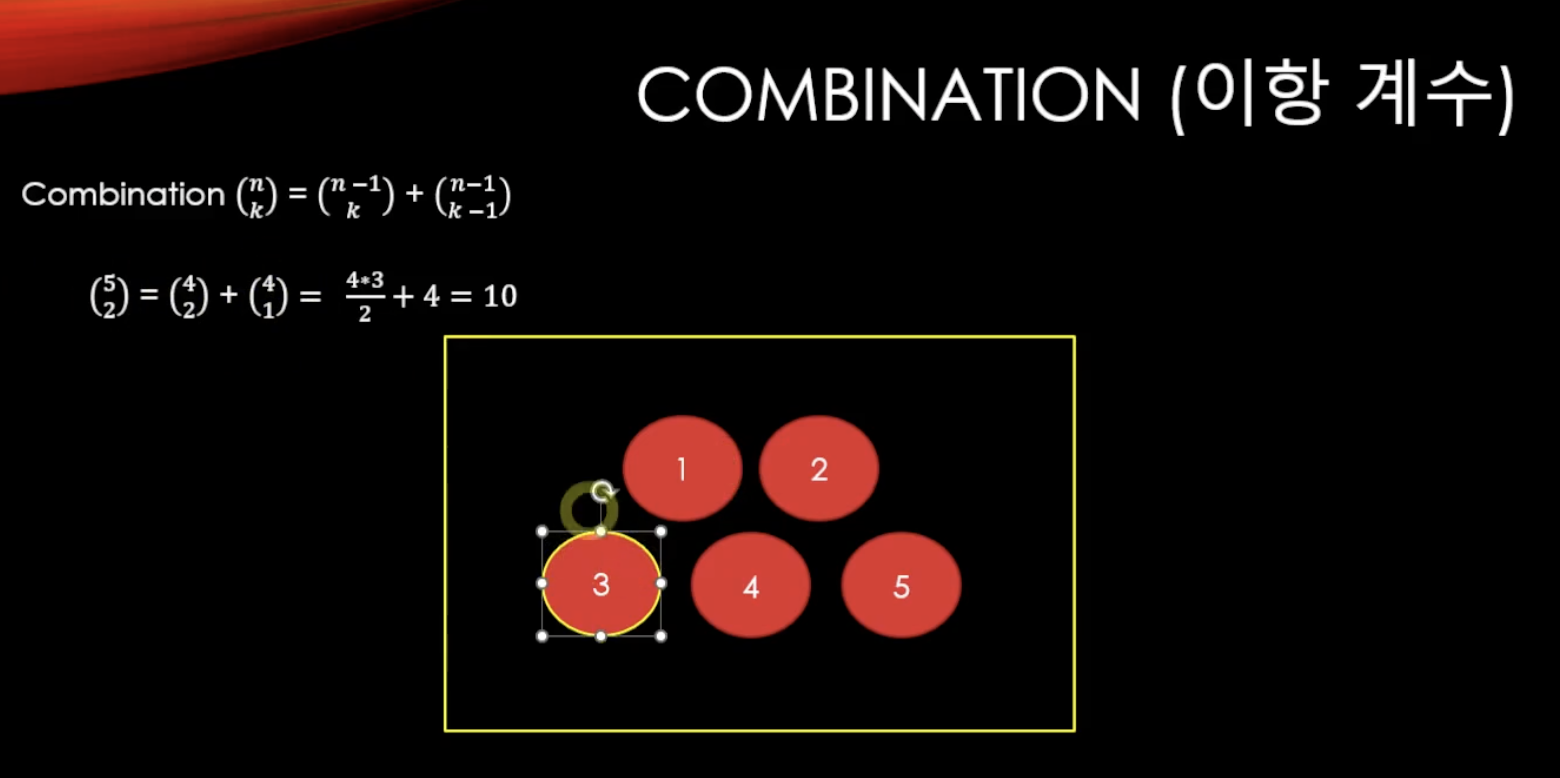
이항 계수 Combination

#include <iostream>
#include <windows.h>

int combination(int n, int r)

{
	if (r==0 || n==r)
    	return 1;
    
    return combination(n-1, r-1) + combination(n-1, r);
}

int main()
{
	__int64 start = GetTickCount64();
	int lotto = combination(45, 6);
    __int64 end = GetTickCount64();
    cout << end - start << "ms" << endl;
}

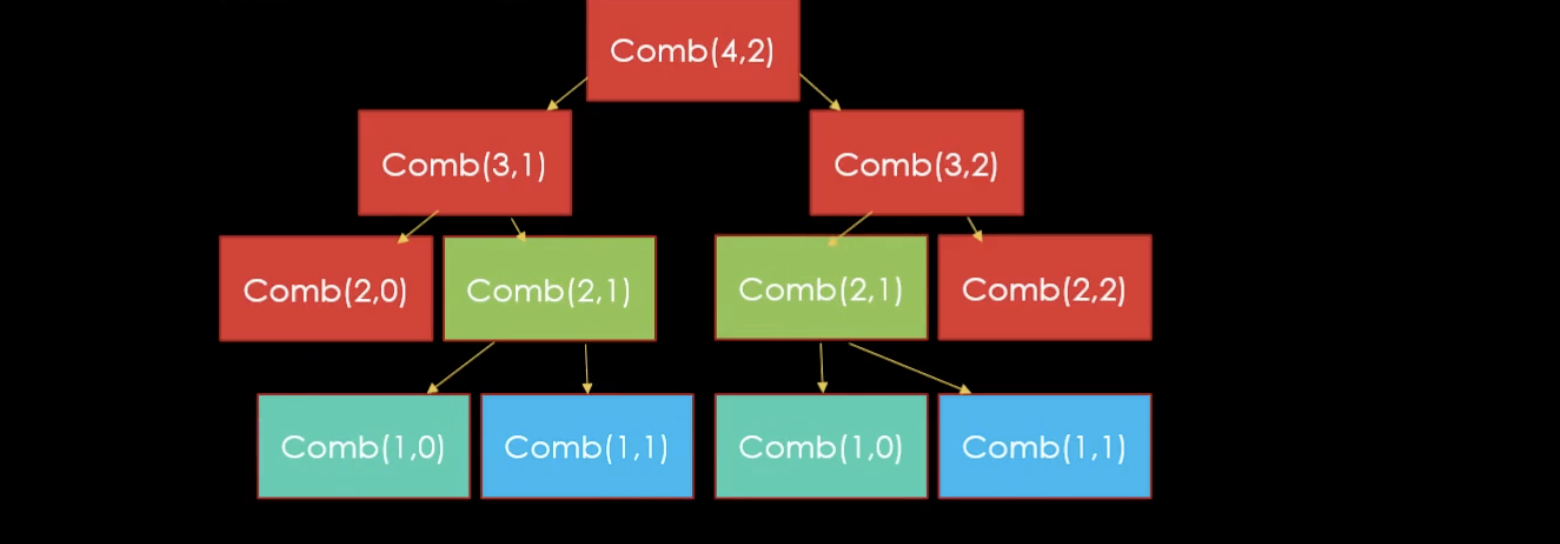
memoization

cache를 사용하면 반복된 계산을 하지 않아도 된다.
이것이 바로 DP 이다. 게임 알고리즘을 만들 때 필요하진 않으나 (주로 인공지능에서 많이 쓰이는!)
계산했던 걸 또다시 무식하게 계산해야 할 경우에 응용하면 좋지 않을까!

그럼 어떻게 응용하느냐? 어떻게 cache를 만들까?
memoization 이라고 한다.

#include <iostream>
#include <windows.h>

int cache[50][50]

int combination(int n, int r)

{
	// 기저 사례
	if (r==0 || n==r)
    	return 1;
    
    // 이미 답을 구한 적이 있다면 바로 반환
    // 참조값(&)으로 해주면 매번마다 복사해줄 필요가 없다 ~
    int& ret = cache[n][r];
    if (ret != -1)
    	return ret;
    
    return ret = combination(n-1, r-1) + combination(n-1, r);
}

int main()
{
	// 초기값을 모두 -1 로 초기화한다
    // 0 이나 1 둘 중 하나를 사용할 때 memset를 많이 사용한다
    ::memset(cache, -1, sizeof(cache));
    
	__int64 start = GetTickCount64();
	int lotto = combination(45, 6);
    __int64 end = GetTickCount64();
    cout << end - start << "ms" << endl;
}

활용 예시

/*
+0 집행검
무기 강화 주문서 -> +1 +2 +3 중 하나

+9 집행검 뜨는 경우의 수는?
ex) +1 +2 +3 ... +9
ex) +3 +6 +9
ex) +1 +3 +4 ... +9
*/

int N = 9; // 목표로 하는 강화 레벨
int cache[100]; // Enchant()의 계산 값을 저장하기 위해 사용

// [+num]부터 시작해서, [+N]까지 가는 경우의 수
// 재귀함수 Enchant()는 주어진 num에서 시작하여 강화 레벨 N에 도달할 수 있는 경우의 수를 계산한다.
int Enchant(int num)
{
	// 기저 사례
    if (num > N)
    	return 0;
    if (num == N)
    	return 1; // 목표 레벨에 도달할 수 있는 유효한 방법이 하나뿐이다
        
    // 캐시
    int& ret = cache[num]; // 캐시 값을 간단히 액세스, 업데이트하기 위해
    if (ret != -1) // 이미 캐시에 계산되어 저장되어있다면
    	return ret; // 추가적인 계산없이 캐시된 값을 반환
        
    // 적용
    // 무기 강화 주문서가 +1, +2, +3 wnd gkskfh wmdrkgkamfh~
    return ret = Enchant(num+1) + Enchant(num+2) + Enchant(num+3);
}

int main()
{
	memset(cache, -1, sizeof(cache));
    int ret = Enchant(0);
	cout << ret << endl;
}