🥇 우선순위 큐
우선순위가 높은 데이터부터 꺼내는 자료구조로, 각 요소가 우선순위를 가집니다.
-
그냥 Queue 는 선형 자료구조인데, Priority Queue 는 비선형 자료구조이다. (선형 자료구조는 자료를 순차적으로 나열한 형태로 배열, 연결 리스트, 스택, 큐가 있다)
-
이와 반대로 비선형 자료구조는 하나의 자료 뒤에 다수의 자료가 올 수 있는 형태로 트리, 그래프가 있다.
-
우선순위 큐는 우선순위가 높은 데이터가 먼저 나오는 자료구조다.
-
큐와 동일하게 데이터 삽입과 삭제 연산을 지원한다. 데이터 삭제 연산을 수행하면 우선순위가 가장 높은 데이터를 얻을 수 있다.
-
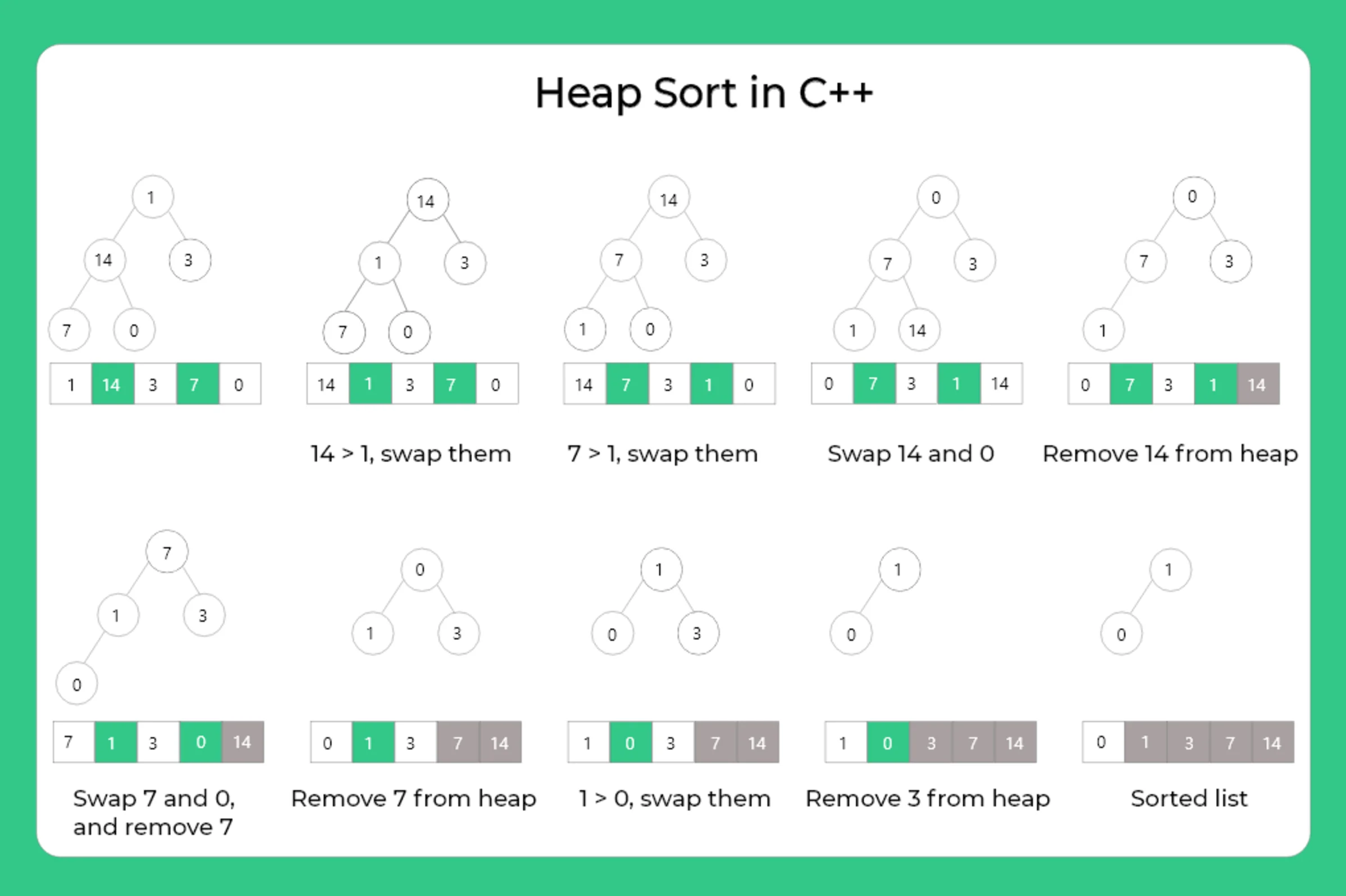
우선순위 큐를 활용해 힙 정렬 구현과 Dijikstra 알고리즘 구현에 사용할 수 있습니다.
-
우선순위 큐는 주로 Heap을 이용해 구현됩니다.
- 이진 트리 중에서도 🎄완전 이진 트리🎄의 한 종류로, (참고: 완전 이진 트리라면 균형잡힌 트리구조이다)
- 최대 힙과 최소 힙이 있어서 최댓값 또는 최솟값을 빠르게 찾을 수 있는 자료구조입니다.
- 참고로, 단순히 N개의 데이터를 힙에 넣었다가 모두 꺼내는 작업은 정렬과 동일하다 (힙 정렬)
⚠️ 주의 사항
C++의 우선순위 큐(std::priority_queue)는 기본적으로 내림차순으로 정렬된다.
이는 기본적으로 std::less 라는 predicate를 사용한다.
그러나 만약 오름차순으로 정렬하고 싶다면,
std::greater를 사용하여 우선순위 큐를 선언해야 한다.
예를 들어:
std::priority_queue<int, std::vector<int>, std::greater<int>> minHeap;
// 오름차순으로 정렬됨위 코드에서 std::greater<int>는 오름차순 정렬을 위한 predicate 이다.
이렇게 선언된 우선순위 큐는 가장 작은 요소가 우선순위를 가지게 된다.
또한비교함수 사용 시에는 구조체나 클래스 형식으로 operator()를 오버라이딩 해야하며, 아래 코드와 마찬가지로 부등호가 > 인 경우 (return a.first > b.first;) 오름차순이 됨.
코드
#include <iostream>
#include <queue>
#include <algorithm>
using namespace std;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
// default(descending) priority (내림차순)
priority_queue<int> queue;
// ascending priority (오름차순)
priority_queue<int, vector<int>, greater<int>> minQueue;
// custom priority (비교함수)
class cmp {
public: bool operator() (const pair<int, int> a, const pair<int, int> b)
{
// 오름차순
if (a.second == b.second)
{
return a.first > b.first;
}
return a.second > b.second;
}
};
priority_queue<pair<int, int>, vector<pair<int, int>>, cmp> pairQueue;
return 0;
}구현 방법
우선순위 큐를 구현하는 방식은 배열, 연결 리스트, 완전 이진 트리인 Heap이 있다.
각 구현 방식에 따라서 시간 복잡도를 비교한 내용은 다음과 같다.
일반적으로 가장 효율적인 방식인 Heap을 사용한다.
| 구현방법 | ⏰ 삽입 | ⏰ 삭제 |
|---|---|---|
| 배열 (unsorted array) | O(1) | O(n) |
| 연결리스트 (unsorted linked list) | O(1) | O(n) |
| 배열 (sorted array) | O(n) | O(1) |
| 연결리스트 (sorted linked list) | O(n) | O(n) |
| 완전이진트리인 힙 (heap) | O(log n) | O(log n) |
배열의 경우
- 삽입하는데 ⏰
O(1)이 걸리나, - 삭제 시 우선순위가 가장 높은 데이터를 찾기 위해 선형 탐색을 해야 해서 ⏰
O(N)의 시간 복잡도가 소요된다.
최대 힙 구현 (Heapify)
완전 이진 트리의 높이 logN 이 곧 검색 횟수이다.
#include <iostream>
using namespace std;
#include <vector>
#include <queue>
template<typename T>
class PriorityQueue
{
public:
// ⏰ O(logN)
void push(const T& data)
{
heap.push_back(data);
// 👑 COUP' 👑
int now = static_cast<int>(heap.size()) - 1;
// 루트 노드까지
while (now > 0)
{
// 부모 노드와 비교해서 heap[now]가 더 작으면 COUP 패배, 빠져나온다
int next = (now - 1) / 2;
if(heap[now] < heap[next])
break;
// 부모 노드와 비교했을 때, heap[now] 가 더 크면 COUP 진행시켜, 데이터 교체!
::swap(heap[now], heap[next]);
now = next; // 타고타고 올라가도록 한다
}
}
// ⏰ O(logN)
void pop()
{
// 👑 REVERSE COUP' 👑
// 최대값(루트) 을 먼저 제거한다, 마지막 노드를 루트로 옮긴다
// 역도장깨기를 할 때는 그냥 도장깨기보다 조금 더 까다로운 이유가,
// 자식이 왼쪽, 오른쪽 둘 다 봐야 해서
// 두 자식 중 더 큰 아이와 바꿔줘야 한다는 점을 만들어줘야 한다.
heap[0] = heap.back();
heap.pop_back()
int now = 0;
while true()
{
int left = 2 * now + 1;
int right = 2 * now + 2;
// 리프에 도달한 경우, 빠져나온다. 더 이상 갈 구석이 없기 때문이다.
if (left >= (int)heap.size())
break;
// (1) next 가 변화가 없건 == 자식이 다 작다
int next = now;
// (2) next 가 left 가 되건 == 왼쪽 자식이 나보다 크다
if (heap[next] < heap[left]) next = left;
// (3) next 가 right 가 되건 == 오른쪽 자식이 나보다 크다
if (right < heap.size() && heap[next] < heap[right])
next = right;
// (1) left, right 둘 다 now 값보다 작으면 종료
if (next == now)
break;
// (2),(3) 그게 아니면 역쿠데타 ㄱㄱ
::swap (heap[now], heap[next]);
now = next;
}
}
// ⏰ O(1)
T& top()
{
return heap[0];
}
// ⏰ O(1)
bool empty()
{
return heap.empty();
}
private:
vector<T> heap;
};
int main()
{
vector<int> v;
PriorityQueue<int> pq;
}힙 정렬 (with 우선순위큐)
이 방법을 사용하면 별도의 최소 힙 구현없이 기본 제공되는 최대 힙을 사용하여 오름차순 정렬을 할 수 있습니다.
#include <bits/stdc++.h>
using namespace std;
void heapSort(vector<int>& arr) {
priority_queue<int> h; // 최대힙 (큰 값부터 나오는 내림차순)
// 모든 원소를 차례대로 힙에 삽입
for (int i = 0; i < arr.size(); i++) {
h.push(-arr[i]); // 데이터를 넣을 때와 뺄 때 -부호를 사용하면 오름차순 정렬로 정렬이 가능하다.
}
// 힙에 삽입된 모든 원소를 차례대로 꺼내어 출력
while (!h.empty()) {
printf("%d\n", -h.top()); // 30 20 10
h.pop();
}
}
int n;
vector<int> arr;
int main() {
cin >> n; // 3
for (int i = 0; i < n; i++) {
int x;
scanf("%d", &x); // 10 20 30
arr.push_back(x);
}
heapSort(arr);
}