목적 : 데이터를 빨리 찾고 싶다
이진 탐색
반으로 나눌 때마다 절반으로 줄어들므로, 정렬된 배열 에 특정원소가 있는지를 확인하는 것을
O(logN)만에 해결하는 알고리즘이다. C++에서는 내장된 라이브러리lower_bound,upper_bound를 활용해 구현할 수 있다.
-
시간복잡도
O(logN) -
재귀함수를 사용하지 않으면 while 을 사용하면 된다
-
재귀함수를 사용하겠다면 BinarySearch 인자에 Start, End 를 추가해주자
-
한계점
-
정렬이 균형있게 되기 어려우며,
-
vector 배열의 특성상 중간 삽입 / 삭제가 어렵다.
- 고정적인 상황에서만 사용할 수 있다는 한계가 있다.
-
연결리스트로 이진탐색을 만들 수 있을까?
- No! 임의 접근이 불가하다.
-
#include <iostream>
using namespace std;
#include <vector>
#include <list>
#include <queue>
#include <map>
vector<int> numbers;
void BinarySearch(int N) // N은 우리가 찾을 번호
{
int left = 0;
int right = numbers.size() - 1;
while (left <= right) // 이 조건 잊지 말기!
{
cout << "탐색 범위 : " << left << "~" << right << endl;
int mid = (left + right) / 2;
if (N < numbers[mid])
{
right = mid - 1;
}
else if (N > numbers[mid])
{
left = mid + 1;
}
else // 값이 같다는 것이니, 찾았다는 의미!
{
cout << "찾았다!" << endl;
break;
}
}
}
int main()
{
numbers = {1, 8, 15, 23, 32, 44, 56, 63, 81, 91};
BinarySearch(81);
}
이진 탐색 트리 ⭐️
이진 탐색에서 vector 의 특성상 중간 삽입 / 삭제가 어렵다 라는 명확한 한계가 있으니 이진 탐색 트리라는 방안을 살펴보자.
탐색 이라는 의미는
- 왼쪽으로 가면 나보다 작은 아이들이,
- 오른쪽으로 가면 나보다 큰 아이들이 있다는 의미이다.
이진탐색 트리의 문제는 균형 이다.
- 시간복잡도가
O(logN)이지만 - 균형이 잡히지 않으면 결국 연결 리스트와 같은 꼴이 되고, 시간복잡도 또한
O(N)으로 최악이 된다.
그래서 등장한 것이 균형을 자동적으로 맞춰주는 AVL, 레드 블랙 트리이다.
// BinarySearchTree.h
#pragma once
struct Node
{
Node* parent = nullptr;
Node* left = nullptr;
Node* right = nullptr;
int key = 0; // 데이터
};
class BinarySearchTree
{
public:
Node* Search(Node* node, int key);
void Insert(int key); // 노드 생성 후 위치를 골라줘서 넣어주는 행위
// 삭제 기능을 위한 헬퍼 함수들
Node* Min(Node* node); // 어떠한 트리 기준으로 가장 작은 값이 어디?
Node* Max(Node* node); // 어떠한 트리 기준으로 가장 큰 값이 어디?
Node* Next(Node* node); // 그 다음으로 큰 ?
void Replace(Node* u, Node* v); // 삭제할 때 재설정
void Delete(int key);
void Delete(Node* node);
private:
Node* _root = nullptr;
}
// BinarySearchTree.cpp
#include "BinarySearchTree.h"
void BinarySearchTree::Insert(int key)
{
Node* newNode = new Node();
newNode->key= key;
if(_root == nullptr) // 만약 내가 첫 번째 노드라면
{
_root = newNode;
return;
}
// 추가할 위치를 찾기
Node* node = _root;
Node* parent = nullptr;
while (node)
{
parent = node;
if (key < node->key)
node = node->left;
else
node = node->right;
}
newNode->parent = parent;
if (key < parent->key)
parent->left = newNode;
else
parent->right = newNode;
}
Node* BinarySearchTree::Search(Node* node, int key)
{
if (node == nullptr || key == node->key)
return node;
if (key < node->key)
return Search(node->left, key); // 재귀
else
return Search(node->right, key);
}
/* 트리의 최솟값 */
Node* BinarySearchTree::Min(Node* node)
{
if (node == nullptr)
return;
while (node->left)
node = node->left;
return node;
}
/* 트리의 최댓값 */
Node* BinarySearchTree::Max(Node* node)
{
if (node == nullptr)
return;
while (node->right)
node = node->right;
return node;
}
/* 어떠한 노드를 기준으로 "그 다음으로 큰 데이터"는 어느 노드에 있는지? */
Node* BinarySearchTree::Next(Node* node)
{
// 1번째 경우: 한 칸 오른쪽으로 가고 거기서 제일 작은 값을 추출
if (node->right)
return Min(node->right);
// 2번째 경우: 조상 중 나를 왼쪽 자식으로 들고 있는 조상을 만날 때까지 올라간다
Node* parent = node->parent;
while (parent && node == parent->right)
{
node = parent;
parent = parent->parent;
}
return parent;
}
/* 재배치*/
void BinarySearchTree::Replace(Node* u, Node* v)
{
if (u->parent == nullptr)
_root = v;
else if (u == u->parent->left)
u->parent->left = v;
else
u->parent->right = v;
if (v)
v->parent = u->parent;
delete u;
}
/* 키 삭제 */
void BinarySearchTree::Delete(int key)
{
Node* deleteNode = Search(_root, key);
Delete(deleteNode);
}
/* 노드 삭제 */
void BinarySearchTree::Delete(Node* node)
{
if (node == nullptr)
return;
// 삭제할 노드의 자식이 왼쪽에 없고 오른쪽에 있는 경우
if (node->left == nullptr)
{
Replace(node, node->right);
}
// 삭제할 노드의 자식이 왼쪽에 있고 오른쪽에 없는 경우
else if (node->right == nullptr)
{
Replace(node, node->left);
}
// 삭제할 노드의 자식이 양쪽의 2개인 경우
else
{
Node* next = Next(node);
node->key = next->key;
Delete(next);
}
}
레드 블랙 트리
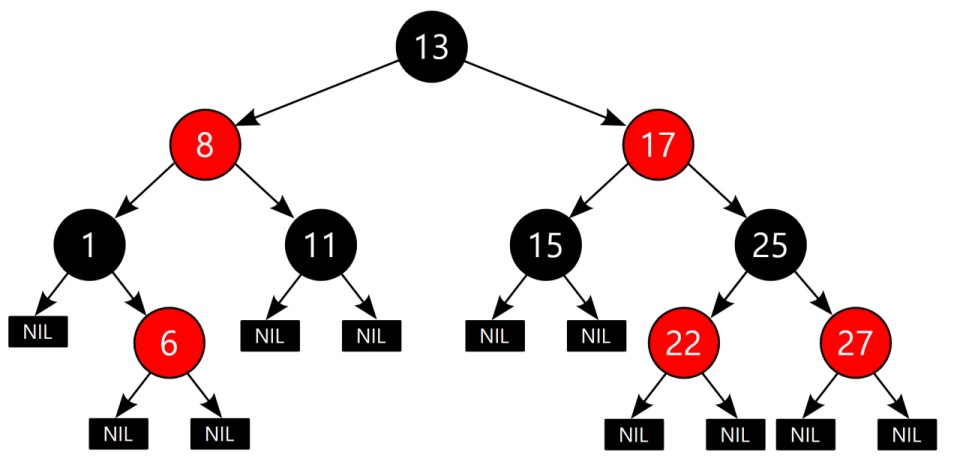
1) 노드는 Red or Black
2) Root 는 Black
3) Leaf (NIL) 는 Black (NIL 은 Null Dummy 라고 생각해도 좋다)
4) Red 노드의 자식은 항상 Black (연속해서 Red-Red 등장할 수 없음)
5) 어떤 노드로부터 그에 속한 하위 리프 노드에 도달하는 모든 경로에는 같은 개수의 블랙 노드를 만난다. -> 이걸 맞추기 위해 아주 난리를 쳐야 한다.
+) 새로 추가된 신입 노드는 Red
균형이 맞춰지는 알고리즘이라는 것...
