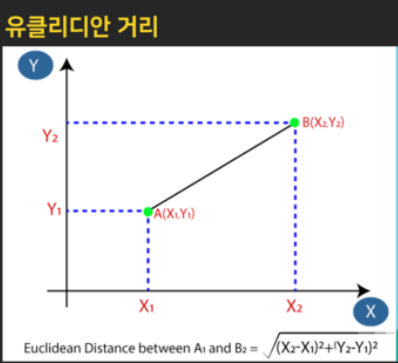
kNN은 데이터를 분류하고 새로운 데이터 포인트의 카테고리를 결정할 때 K개의 가장 가까운 포인트를 선점하고, 그중 가장 많이 선택된 포인트의 카테고리로 새로운 데이터를 분류하는 방법인데, 거리를 측
정할 때 '유클리디안 거리' 계산법을 사용함.
예를 들면, k = 3, 새로운 데이터는 X이고, A분야, B분야가 있다.
3 안에 A가 2개, B가 1개 이면 X는 'A분야'라고 분류할 수 있다.
하지만 만약 k의 개수가 홀수가 아닌 짝수 일때는 곤란한 상황이 나올 수 있다. 만약 위와 같은 상황에서 k의 개수가 4개이고 A분야가 2개, B분야도 2개이면 새로운 데이터 X를 분류할 수 없는 상황이 만들어진다.
구현시 주의할 점
- KNN 알고리즘과 같이 거리기반 모델의 경우 표준화가 필요함. A와 B의 분포가 다르면 두 변수의 차이를 해석하기가 어려움. 그래서 변수 값을 표준 범위로 재조정하기 위해 정규화를 적용해야함.
정규화 방법
1) '최소-최대 정규화'
-> 변수 X의 범위를 0%에서 100%까지로 나타내는 방식. 이런식으로 정규화를 할 시, 범위가 0에서 100만이라도 모든 변수는 0%에서 100% 범위 안에 들어오게 됨.
2) 'z-점수 표준화'
-> 변수 X의 범위를 평균의 위 또는 아래로 몇 표준 편차만큼 떨어져 있는지 관으로 변수를 확대/축소하는 방식임.
코드로 구현
import random
import numpy as np
a = [] # 사과
p = [] # 배
#일반적으로 배가 사과보다 크고 무거움
for i in range(50): #50개의 데이터를 각각 추가함
a.append([random.randint(5,10), random.randint(50,100), 1])
p.append([random.randint(8,15), random.randint(90,120), 0])
# random.randint(a, b) -> 인자로 들어온 a,b 사이의 랜덤한 정수(int)를 반환함(a,b를 포함한 범위임)
# 마지막의 1과 0은 데이터 상에서 사과와 배를 구분하기 위함임
def distance(x, y):
return np.sqrt(pow((x[0]-y[0]),2)+pow((x[1]-y[1]),2))
# sqrt -> numpy에서 제공하는 함수로, 제곱근 배열을 반환
# numpyt.sqrt(x, y = None)
# => x : 입력배열, y : y가 주어지면 결과는 y에 저장됨. y는 x와 같은 모양이어야함.
# pow(x, y) = x의 y승 = x ** y
def knn(x,y,k):
result = []
cnt = 0
for i in range(len(y)):
result.append([distance(x,y[i]),y[i][2]])
result.sort()
for i in range(k):
if result[i][1] == i:
cnt += 1
if cnt > (k/2):
print("pear")
else:
print("apple")
size = input("크기 : ")
weight = input("무게 : ")
num = input("k : ")
new = [int(size), int(weight)]
knn(new, a+p, int(num))산점도 그리기
import matplotlib.pyplot as plt
%matplotlib inline
aa = np.array(a)
pp = np.array(p)
for i,j in aa[:,:2]:
plt.plot(i,j,'or')
for i,j in pp[:,:2]:
plt.plot(i,j,'ob')
plt.plot(int(size), int(weight), 'og')
plt.show()