
경사하강법이란
- 경사 하강법은 1차 근삿값 발경용 최적화 알고리즘이다. 기본 개념은 함수의 기울기(경사)를 구하고 경사의 반대 방향으로 계속 이동시켜 극값에 이를 때까지 반복시키는 것이다. (위키 백과 정의)
- 옵티마이저(Optimizer)의 한 종류이다.
- 간단하게 loss function의 최소값을 만드는 파라미터를 찾는데 사용된다. loss(오차)가 가장 낮은 지점을 찾게 된다.
- 경사 하강법은 간단하게 생각해서 그래프에서 가장 아래에 있는 꼭짓점의 값을 찾아가는 알고리즘이라고 생각하면 된다.
경사하강법을 사용하는 이유
- 일반적으로 경사하강법은 함수의 최솟값을 찾아야 하는 상황에서 사용된다. 인공지능의 경우 최적의 학습 패턴을 위해 자신의 파라미터(Parameter)를 검증해야 하며, 검증 과정에서 손실 함수를 사용한다. 검증 과정에서 손실 함수의 값이 가장 낮은 파라미터를 발견했다면 해당 파라미터가 최적의 파라미터임이 검증 된 것이다.
경사 하강법의 문제점
- 적절한 Step Size(또는 학습률(Learning rate)
- Local Minima
적절한 Step Size
- Step Size를 크게 잡은 경우, 한 번에 이동하는 크기가 커지게 되므로 빠르게 수렴할 수 있다는 장점이 있다. 그렇다고 해서 Step Size의 크기를 과도하게 설정하면 손실 함수의 최솟값을 계산하기 어려워질 수 있으며 함수의 값이 커지는 방향으로 최적화가 진행될 수 있어 주의해야 한다.
- Step Size를 너무 작게 설정한 경우, 발산하지 않을 수 있다는 점이 있지만, 최적의 파라미터를 탐색할 때 소요되는 시간이 오래 걸릴 수 있다는 단점이 존재한다.
- 따라서 적절한 Step Size(Learning rate)를 설정해야 한다.
Local Minima
- 가장 아래의 꼭짓점이 아닌 다른 꼭짓점을 최적의 파라미터로 착각을 하는 경우이다.
- 실제로 최적의 파라미터를 찾기 위해 Global Minimum을 찾아야 하지만, 경사 하강법의 특성상 알고리즘이 시작되는 파라미터 위치가 랜덤이므로 특정한 경우에서 Local Minima에 빠지게 되어 헤어나오지 못하는 상황이 발생할 수도 있다.
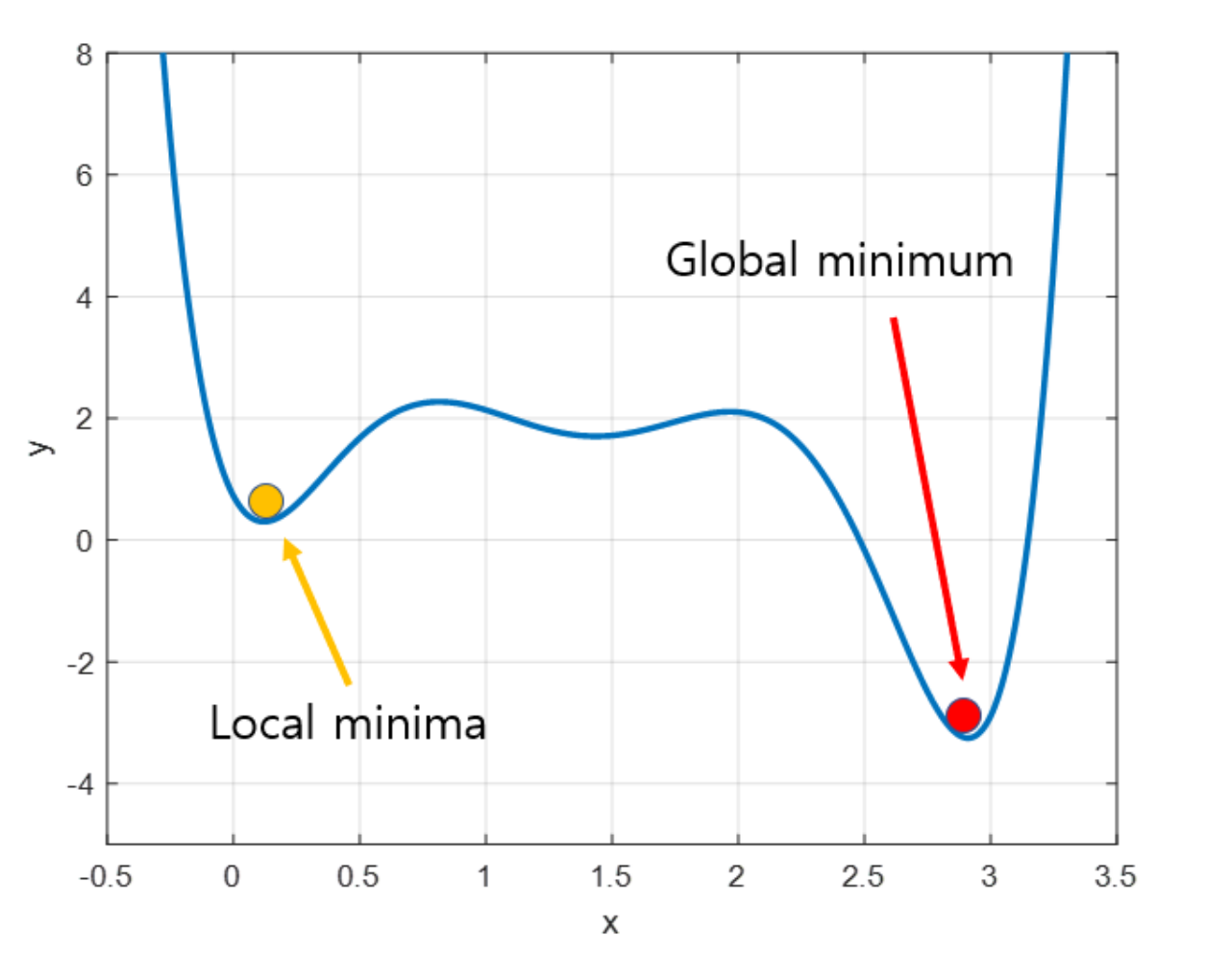
참고


