
손실 함수
- 머신러닝이나 딥러닝 모델에 예측한 값과 실제 값의 차이를 측정하는 함수이다. 이를 통해 모델의 성능을 평가하고, 모델이 어떤 방향으로 개선되어야 할지 알려주는 역할을 한다. 손실함수의 값을 최소화하는 것이 모델 학습의 목표라고 할 수 있다.
손실 함수의 종류
평균 제곱 오차 (Mean Squared Error, MSE)
- 예측 값과 실제 값의 차이를 제곱한 후 평균을 구하는 방식
- 0에 가까울수록 추측한 값이 원본에 가까운 것이기 때문에 정확도가 높다고 할 수 있음
- 예측값과 실제 값의 차이를 제곱하기 때문에, 이상치에 대해 민감하다. 즉, 정답에 대해 예측값이 매우 다른 경우, 그 차이는 오차 값에 상대적으로 크게 반영된다.
- 수식 표현
- : i번째 학습 데이터의 정답
- : i번째 학습 데이터로 예측한 값
- 아래와 같은 그래프가 그려진다.
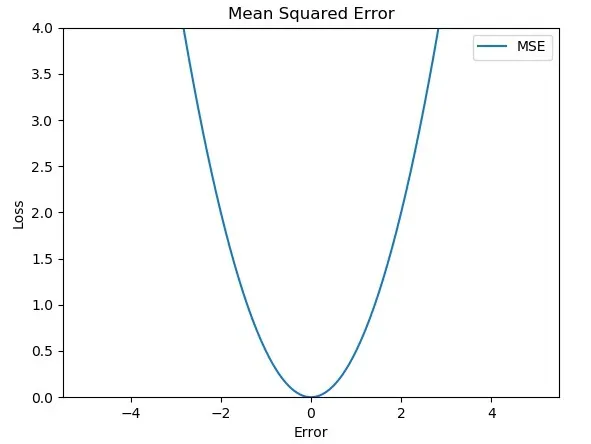
특징
오차 대비 큰 손실 함수의 증가폭
- 오차가 커질수록 손실 함수 값이 빠르게 증가하는 특징이 있음
- 손실 함수의 크기를 오차의 제곱에 비례하여 변함. 그만큼 미분값이 일정하지 않고 오차가 커질수록 미분값 역시 커질 수 있는 것을 알 수 있음.
회귀 문제에 활용
- MSE는 회귀(Regression) 문제에 자주 활용된다.
이진 교차 엔트로피 손실 (Binary Cross Entropy, BCE)
- 실제 레이블과 모델이 예측한 두 클래스가 속할 확률 사이의 불일치를 측정한다. 특히, 모델이 확신을 가지고 잘못된 예측을 할 때, 큰 패널티를 부여한다.
- 예측 확률과 실제 클래스 사이의 차이를 구하는 방식
- 수식 표현
- y_i : 실제 클래스(0 또는 1)
- : 모델이 예측한 확률값
특징
이진 분류 문제에 활용
- Binary Cross Entropy는 이진 분류 문제에 자주 활용된다.
교차 엔트로피 손실(Cross Entropy Error, CEE)
- 두 확률 분포간의 유사성을 측정하는데 유용하며, 특히 분류 문제에서 자주 사용됨
- 실제 값과 모델의 예측값의 로그 값을 곱하여 모든 데이터에 대해 합산한다. 실제값은 0또는 1의 이진값으로 표현되는 One-Hot 벡터로 사용된다.
- 수식 표현
- i : 데이터의 인덱스
- : 실제 값(참 값)
- : 모델의 예측값(출력값)
예시
다음은 간단한 예시를 통해 CEE를 이해해보겠습니다. 이 예시에서는 주어진 사진이 고양이인지 개인지를 분류하는 이진 분류 문제를 다룹니다.
입력 데이터 : 사진
실제값 (참값) : 고양이인 경우 [1, 0], 개인 경우 [0, 1]
모델의 예측값 : 고양이일 확률 0.8, 개일 확률 0.2 (예시)
이때, CEE를 계산해보면 다음과 같습니다:
고양이인 경우 CEE = -[1 log(0.8) + 0 log(0.2)] = -log(0.8) ≈ 0.223
개인 경우 CEE = -[0 log(0.8) + 1 log(0.2)] = -log(0.2) ≈ 1.609
장단점
장점
- 분류 문제에서 자주 사용되는 손실 함수이며, 클래스 간의 확률적인 유사성을 측정하는데 유용함
- 모델이 출력값과 실제값 사이의 차이를 미분 가능한 연속 함수로 나타내기 때문에, 경사 하강법 등의 최적화 알고리즘에 적용할 수 있다.
단점
- 모델의 예측값과 실제값 사이의 차이에 대해 지나치게 민감할 수 있다. 따라서, 모델이 잘못 예측한 경우 CEE 값이 급격하게 증가할 수 있다.
- 이진 분류 문제에만 사용할 수 있으며, 다중 클래스 분류에는 확장하기 어렵다.






