[인공지능] 역전파 알고리즘 (Back Propagation Algorithm)

SeoTae·2024년 8월 19일

인공지능

목록 보기

18/18

Neural Network 모델의 입력층부터 출력층까지 순서대로 변수들을 계산하고 저장하는 것을 의미
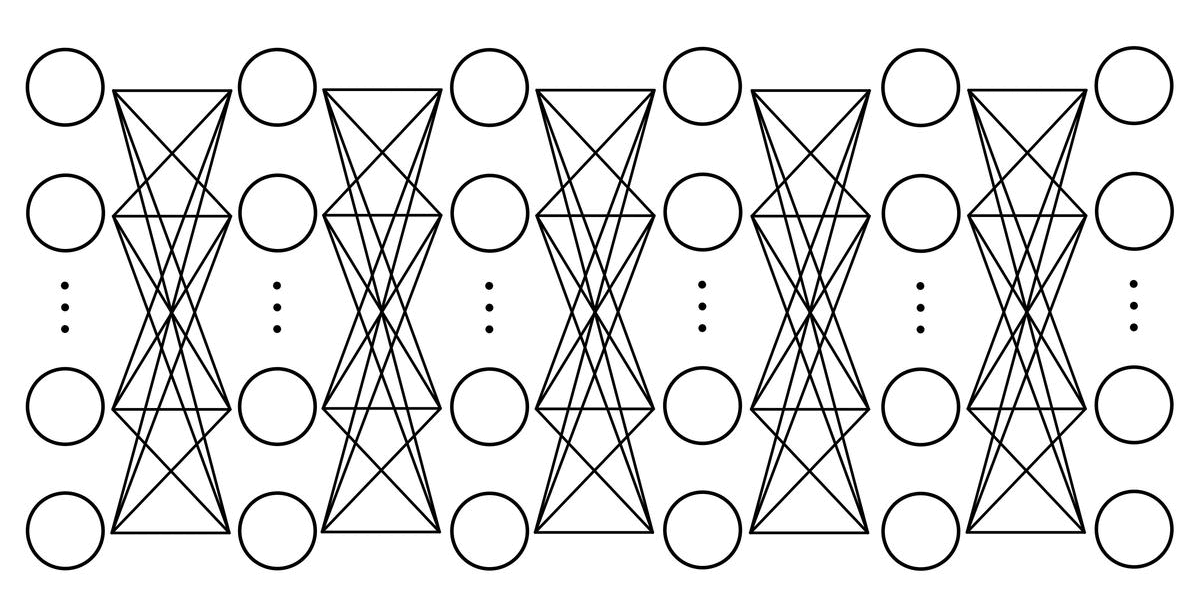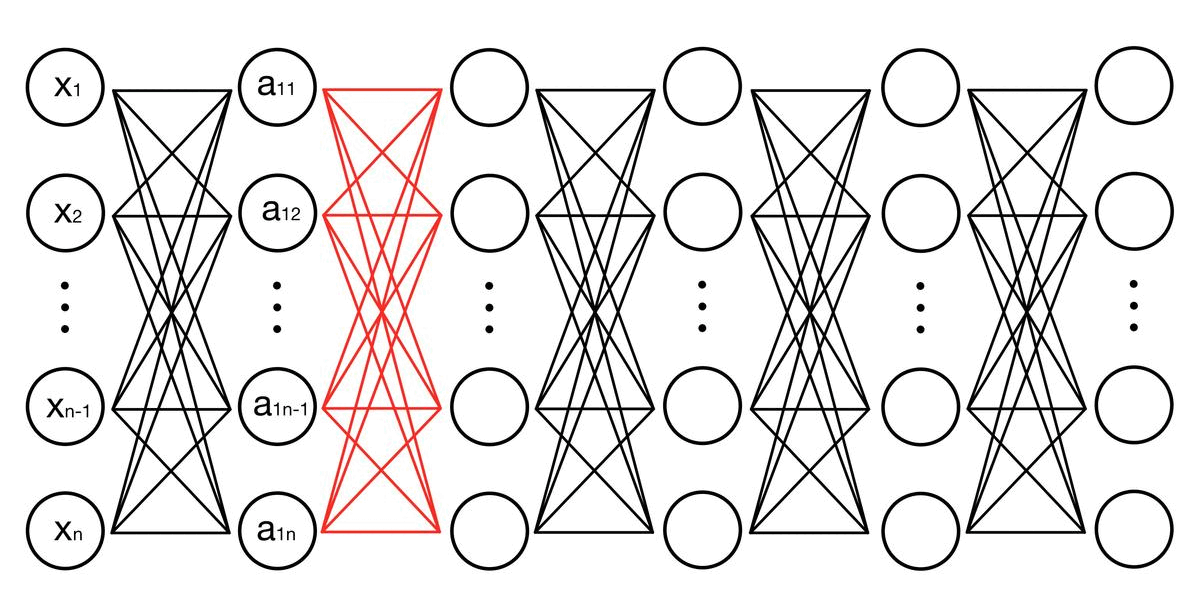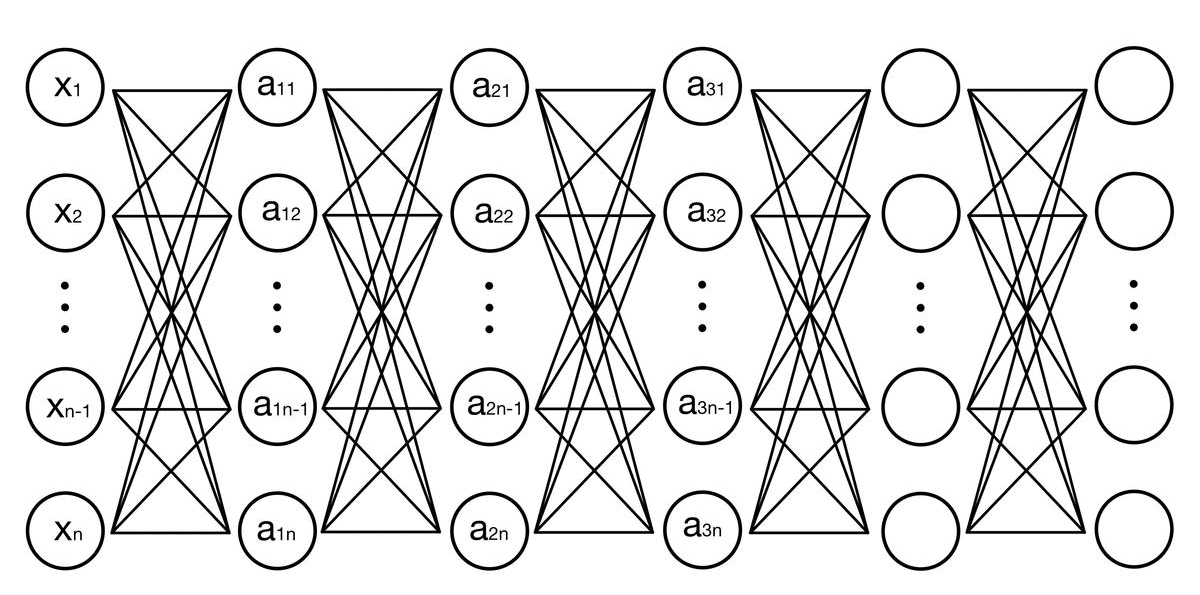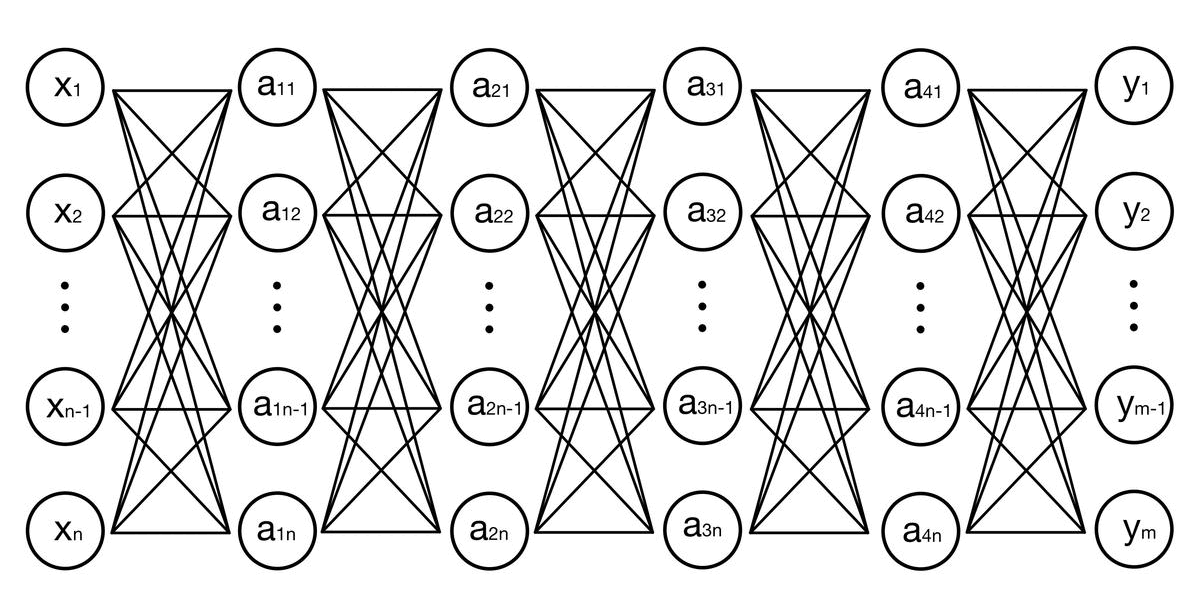
입력층에서 시작하여 은닉층을 거쳐 출력층으로 이동하는 동안, 각 뉴런은 가중치와 활성화 함수를 통해 입력값을 변환하고 다음 뉴런으로 신호를 전달한다.
순전파는 학습 단계가 아니라 입력값을 네트워크에 통과시켜 출력값을 계산하는 과정이다.

두 함수를 합성한 합성 함수의 도함수(derivative)에 관한 공식이다. (위키 백과 정의)
함수 f가 $x_0$ 에서 미분 가능하며, 함수 g가 $f(x_0)$ 에서 미분 가능하며, 아래 식이 성립한다.
$(f \circ g)'(x_0) = f'(g(x_0))g'(x_0)$

f와 g가 구간 i에서 미분 가능하다면, 아래의 식이 성립한다.
$(f \circ g)' = (f' \circ g) \cdot g'$

$y = f(x), u = g(x)$ 로 다시 쓰면, 아래의 식이 성립한다.
$\frac{\partial y}{\partial x} = \frac{\partial y}{\partial u} \cdot \frac{\partial u}{\partial x}$
이런식으로 조금 복잡하게 설명이 되어 있는데, 간단하게 설명하면 아래와 같다.
$Z = (x+y)^2 \\ Z = t^2 \\ t = x + y$ 처럼 나타낼 수 있다.
그렇다면, 직관적으로 x에 대한 Z의 미분 값은 어떻게 구해질까, $2(x+y)$ 가 된다. y에 대한 Z의 미분 값 역시 $2(x+y)$ 가 된다. x와 y에 대한 t의 미분 값이 모두 1이기 때문에, x와 y에 대한 Z의 미분 값이 $2(x+y) \times 1$ 이 된다. 수식으로 나타내면 아래의 규칙성을 확인할 수 있다.
$\frac{\partial z}{\partial x} = \frac{\partial z}{\partial t} \cdot \frac{\partial t}{\partial x} \\ \frac{\partial z}{\partial y} = \frac{\partial z}{\partial t} \cdot \frac{\partial t}{\partial y}$
이미 계산되어 있는 변수를 사용해서 힘든 계산을 변하게 해주는 것이다. 곱셈 법칙 같은 느낌이라고 보면 된다.

Vamos🔥🔥🔥🔥🔥