활성화 함수

• 퍼셉트론(Perceptron)의 출력값을 결정하는 비선형 함수
• 입력 신호의 총합을 출력 신호로 변환하는 함수

활성화 함수의 역할 (비선형 함수여야 하는 이유)

• 입력 신호의 총합이 활성화를 일으키는지를 정하는 역할을 한다. 즉, 앞 뉴런에서 자극이 들어왔을 때 다음 뉴런을 활성화 할지 여부를 판단해준다.
• 신경망의 활성화 함수는 비선형 함수를 사용해야 한다.
• 신경망에서 선형 함수를 이용하면 신경망의 층을 깊게하는 의미가 없어진다. 활성화 함수를 사용하지 않아도 신경망의 층을 깊게하는 의미가 없어진다.

활성화 함수의 종류

1. Sigmoid Function(시그모이드 함수)

• 값이 들어왔을 때, 0~1 사이의 값을 반환한다.
• 큰 음수 값일 수록 0에 가까워지고 큰 양수 값일 수록 1이 된다.
• Sigmoid 함수의 그래프 모양은 아래와 같다.
  

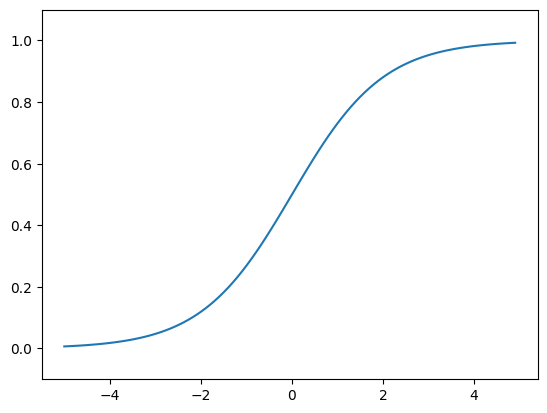
  Sigmoid 함수의 수식 표현
  $\sigma(z) = \frac{1}{1 + e^{-z}}$

• 몇 가지 단점이 있다.

단점 1) 기울기 소멸 문제 (Vanishing Gradient Problem)

• Layer를 많이 쌓을수록 데이터 표현력이 증가해서 학습이 잘 될거 같지만, 실제로는 BackPropagation 과정에서 출력층에서 멀어질수록 Gradient 값이 매우 작아진다. 이러한 현상을 Vanishing Gradient라고 한다.

단점 2) Zero-Centered Problem

• 함수의 결과값의 중심이 0이 아닐 경우 Sigmoid 함수를 통과한 결과값은 모두 동일한 부호값이 나온다. 따라서 Zig-Zag 식의 Parameter update가 발생하기 때문에 수렴 속도가 느려지는 문제점이 있다.

2. tanh Function(하이퍼볼릭 탄젠트 함수)

• tanh 함수는 함수의 중심점을 0으로 옮겨 sigmoid가 갖고 있던 최적화 과정에서 느려지는 문제를 해결함. but, Vanishing Gradient Problem은 여전히 남아있다.
• 값이 들어왔을 때, -1 ~ 1 사이의 값을 반환한다.
• tanh 함수의 그래프 모양은 아래와 같다.
  

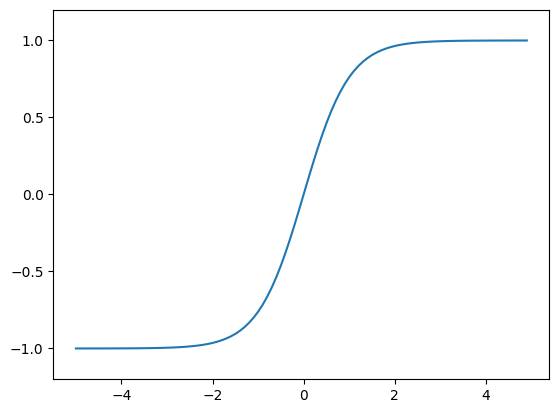
  tanh 함수의 수식 표현
  $tanh(x) = 2\sigma(2x) - 1 \\ tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} \\ tanh(x) = 1 - tanh^2(x)$

3. ReLU Function (Rectified Linear Unit, 경사 함수)

• 가장 많이 사용되는 활성화 함수 중 하나
• Sigmoid와 tanh가 갖는 Vanishing Gradient 문제를 해결하기 위한 함수
• 값이 들어왔을 때, 0보다 크면 들어온 값을 그대로 반환한다.
• ReLU 함수의 그래프 모양은 아래와 같다.
  

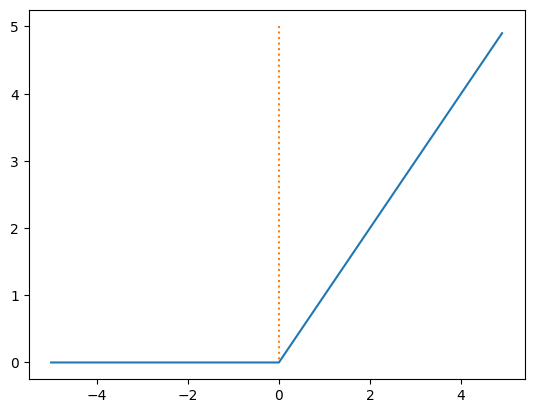
  ReLU 함수의 수식 표현
  $ReLU(x) = max(0, x)$

• Sigmoid, tanh 함수보다 학습이 빠르고, 연산 비용이 적고, 구현이 매우 간단하다는 특징이 있다.
• 몇 가지 단점이 있다.

단점 1) Zero-Centered

• 위의 Sigmoid 함수의 Zero-Centered 문제가 있다.

단점 2) Dead ReLU Problem

• 입력 값이 음수인 경우 기울기가 0이 되어 가중치 업데이트가 안될 수 있다.
• 가중치가 업데이트 되는 과정에서 가중치 합이 음수가 되면 0만 반환되어 아무것도 변하지 않는 현상 발생

단점 3) 미분

• x = 0일 때는 미분이 불가능하다.

가중치 (Weight)

• 각 입력 신호가 결과 출력에 미치는 중요도를 조절하는 매개변수
• 입력 값에 곱해지는 수이며, 입력이 들어온 데이터들 중에서 어떤 feature를 많이 반영하고, 어떤 feature를 덜 반영할지 결정해준다.
• 가중치는 활성화 함수에 따라 기울기를 증가시킨다. 가중치가 커질 수록 그 feature는 모델에 더 많은 영향을 미치게 된다.
• 일반적으로 W로 표기를 한다.

편향 (bias)

• 뉴런의 활성화 조건을 결정하는 매개변수
• 활성화 함수에서 설정된 임계값을 얼마나 쉽게 넘게 할 것인지 결정해준다.
• 편향이 높다면, 그만큼 활성화 함수의 임계값을 넘기 어렵기 때문에 까다로운 모델이 될 것이다. 활성화 함수의 임계값을 넘지 못하면 그 뉴런은 활성화되지 못하기 때문에 간단한 모델이 될 것이다.
• 편향이 작다면, 활성화되는 뉴런이 많아져 복잡한 모델이 된다.
• 일반적으로 b로 표기를 한다.