StyleGAN3

Abstract

• 묘사된 객체의 표면 대신 이미지 좌표에 접착된 것처럼 보이는 세부 사항
  -> Generator 네트워크에서 aliasing 유발하는 부주의한 신호 처리의 근본 원인 추적
• 네트워크의 모든 신호를 연속적인 것으로 해석하여 원치 않는 정보가 계층적 합성 프로세스로 누출되지 않도록 보장하는 아키텍처
• StyleGAN2의 FID와 일치하지만 내부 표현이 크게 다르며 하위 픽셀 스케일에서도 변환 및 회전과 완전히 동일

Aliasing

• 이미지를 픽셀들의 모임으로 이루어진 이산 공간이 않는 연속공간일 떄

  • 이산 : 이미지 크기를 줄이는 작업
  • 연속 : 이미지를 흐려지게 만드는 작업
    -> 해상도가 낮을수록 더 적은 픽셀로 표현 가능
    

• 픽셀들의 모임 뿐만 아니라 연속적인 표현 공간으로 취급

이산표현z와 연속표현z

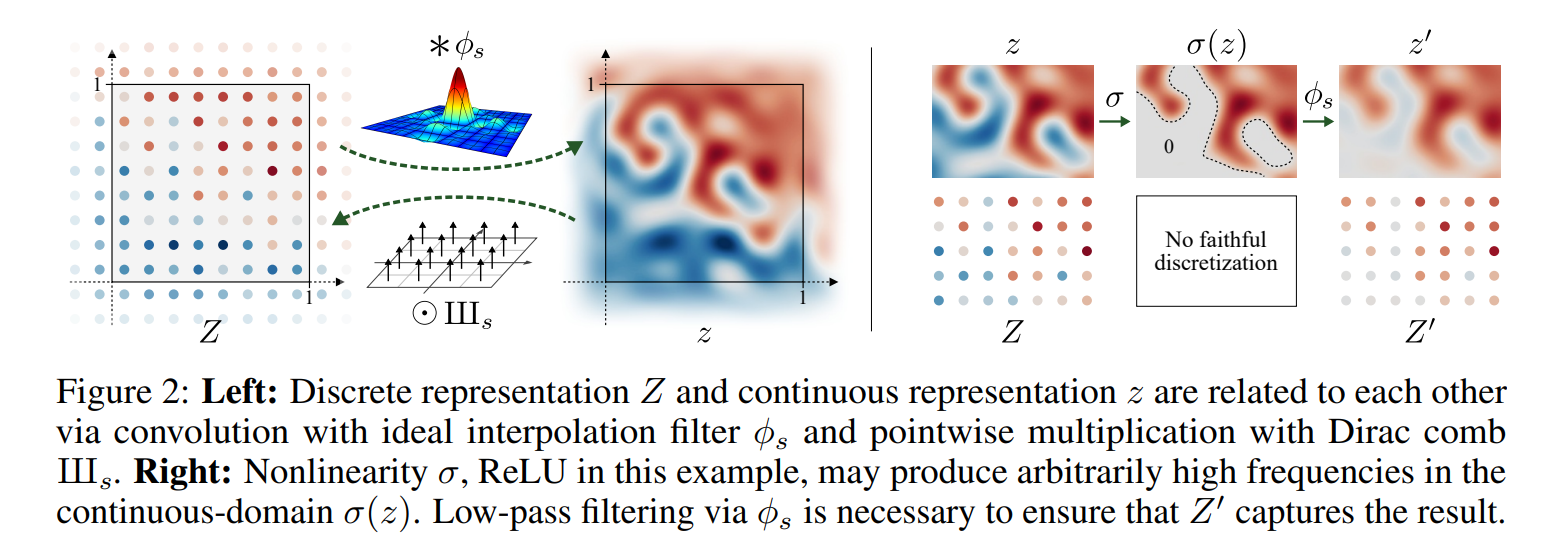
• 싱크 함수를 세로로 한바퀴 돌린것 처럼 생긴 함수를 이산 데이터의 각 픽셀에 컨볼루션 함으로써 이산 표현을 연속 표현으로 변환
• 연속 표현에서 샘플링을 이용해 이산 표현으로 변환
  • 연속 표현으로 변환하는 함수는 연속 표현을 blur하게 만듬으로써 나이쿼스트-샤넌 표본화 정리에서 말한 주파수가 샘플링 주기의 1/2을 넘게 하지 않기 위해 높은 주파수 없앤다

Low Pass Filtering(LPF)

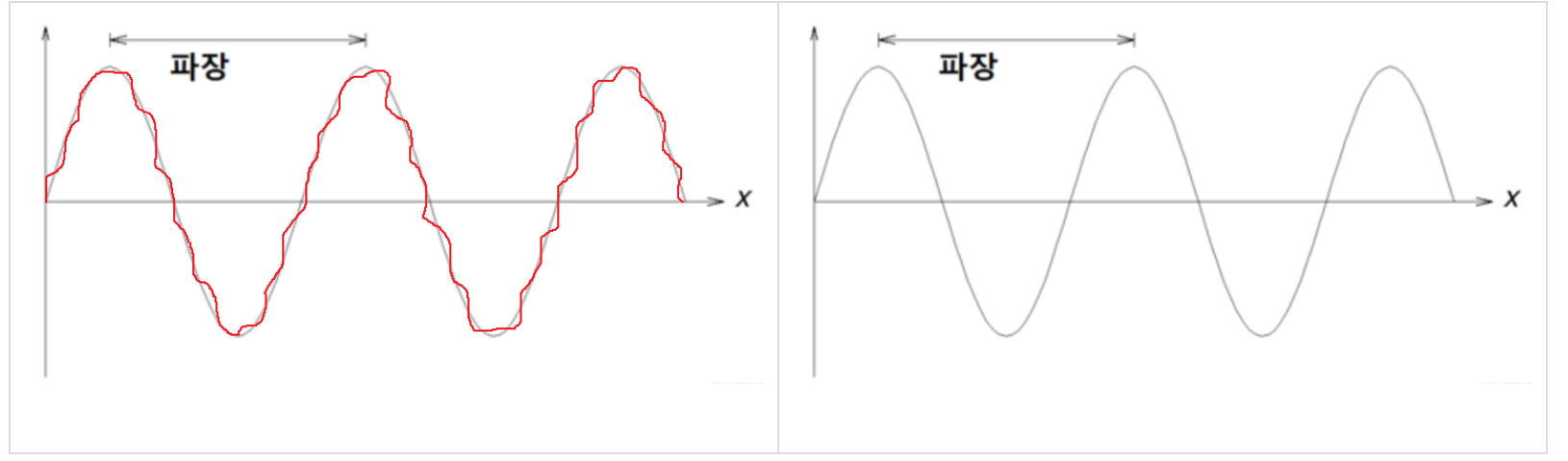
• 높은 주파수의 신호는 파장이 짧기 때문에 세부적인 묘사를 할 수 있게 된다.
  -> 이를 완화함으로써 높은 주파수를 없애 공간이 blur(해상도가 낮음)할 수록 낮은 주파수를 가진다는 것 의미

커널 조건

커널(컨볼루션, 업샘플링, 다운샘플링, 비선형성) 조건 만족해야 한다

• translation과 rotation에 대해서 equivariance해야한다

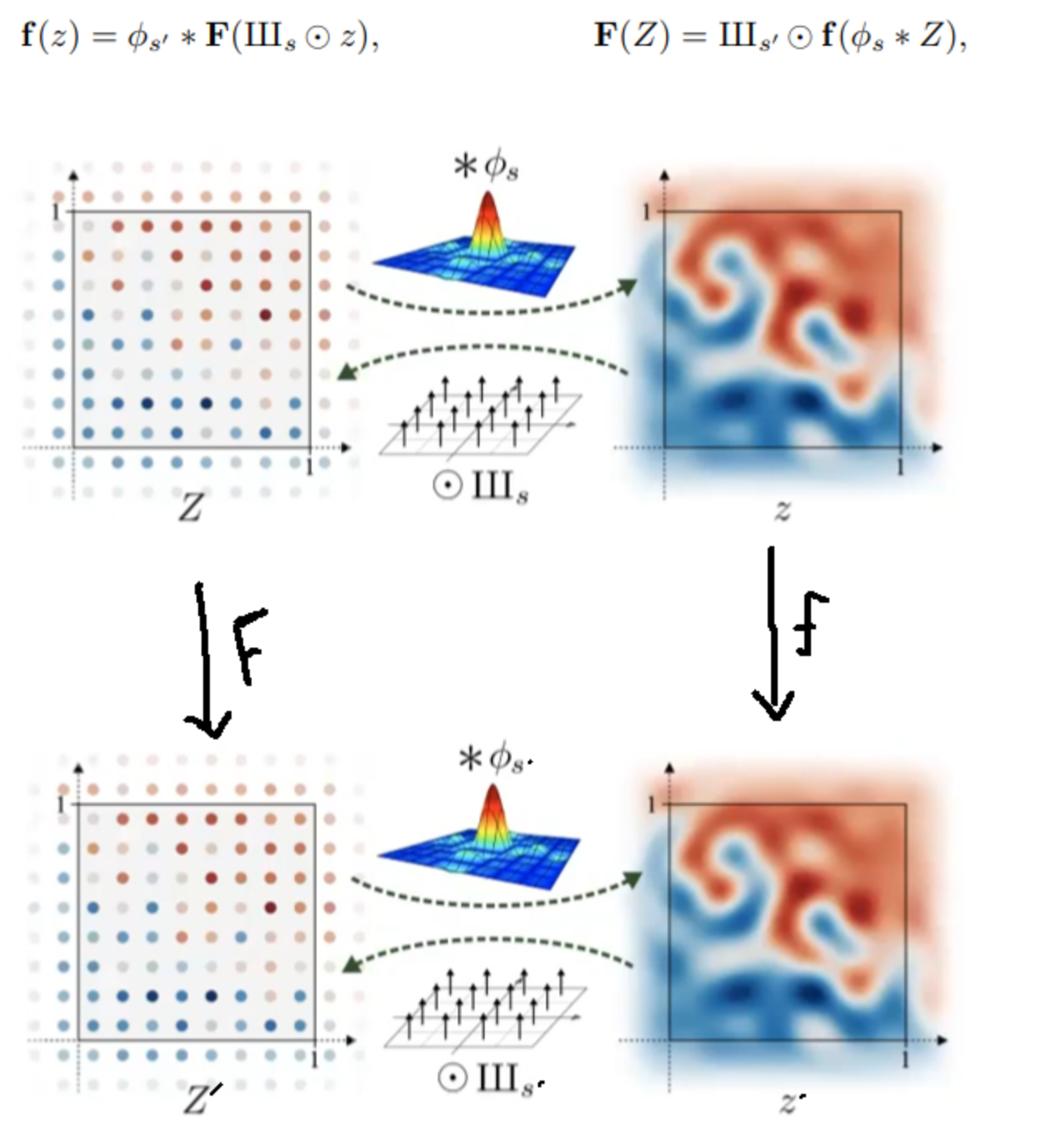
• 이산-연속 표현끼리의 상호변환도 가능해야 한다
  -> 연산 F, f가 연속 표현에서 대역폭 제한을 넘는 주파수 콘텐츠를 도입하면 안된다

conv

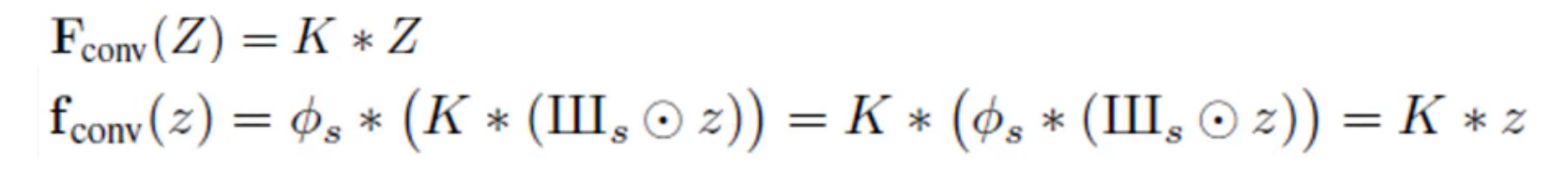
• 컨볼루션은 커널 내에서만 연산하기 때문에 sticking이 없고 컨볼루션 목적 자체가 feature를 분해하는 것에 있기 때문에 주파수가 높아지지 않는다
  
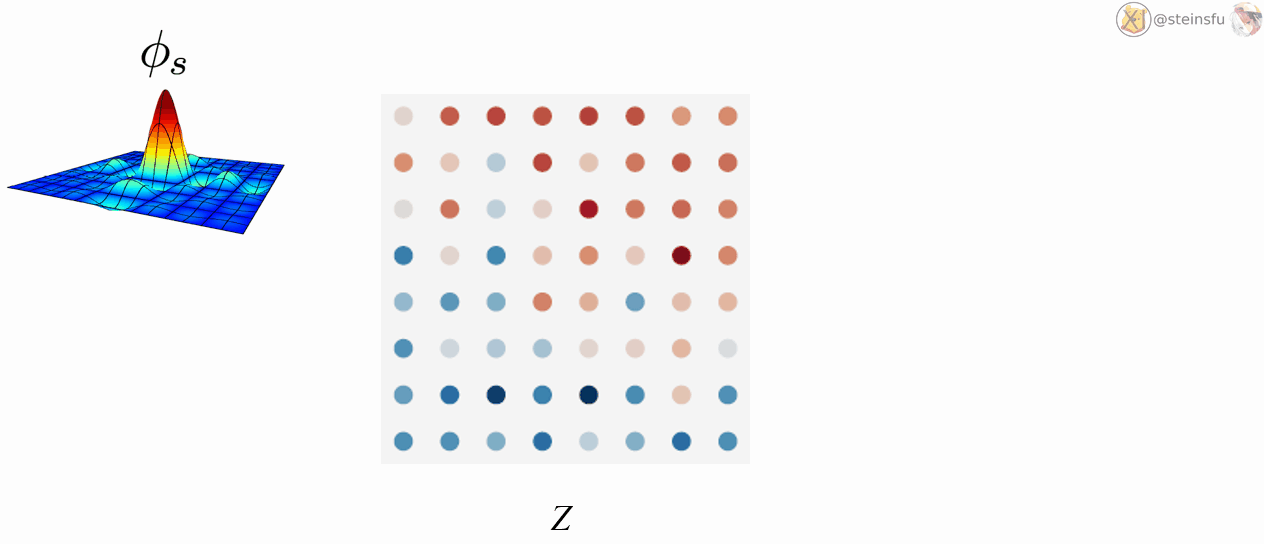
• 이산커널(컨볼루션) k가 rotation에 대해서도 equivariance하려면 방사형 대칭
  

Upsampling

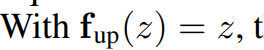
• 위치에 따른 sticking 없음, 새로운 주파수 도입 없음, 연속 표현에서 업샘플링 작업은 sampling rate를 높이기 때문에(연속표현에서 더 많은 표본을 뽑는 것과 같다)
  -> 대역폭 제한 걱정 없음, 연속표현에서는 뭔가가 바뀌지 않는다.

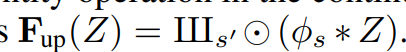
• F를 연속 표현을 통한 연산으로 나타내면 위와 같은데
• 서로 다른 표현간의 변환이 서로 상쇄되었던 컨볼루션 연산과 달리 두 함수의 sampling rate(s)가 다르다
• 구현에서 기존 업샘플링 앨리어싱 억제하는데 충분하지 않기에 기존 방법이 아닌 LPF를 추가한 직접 제작한 필터를 업샘플링에 이용

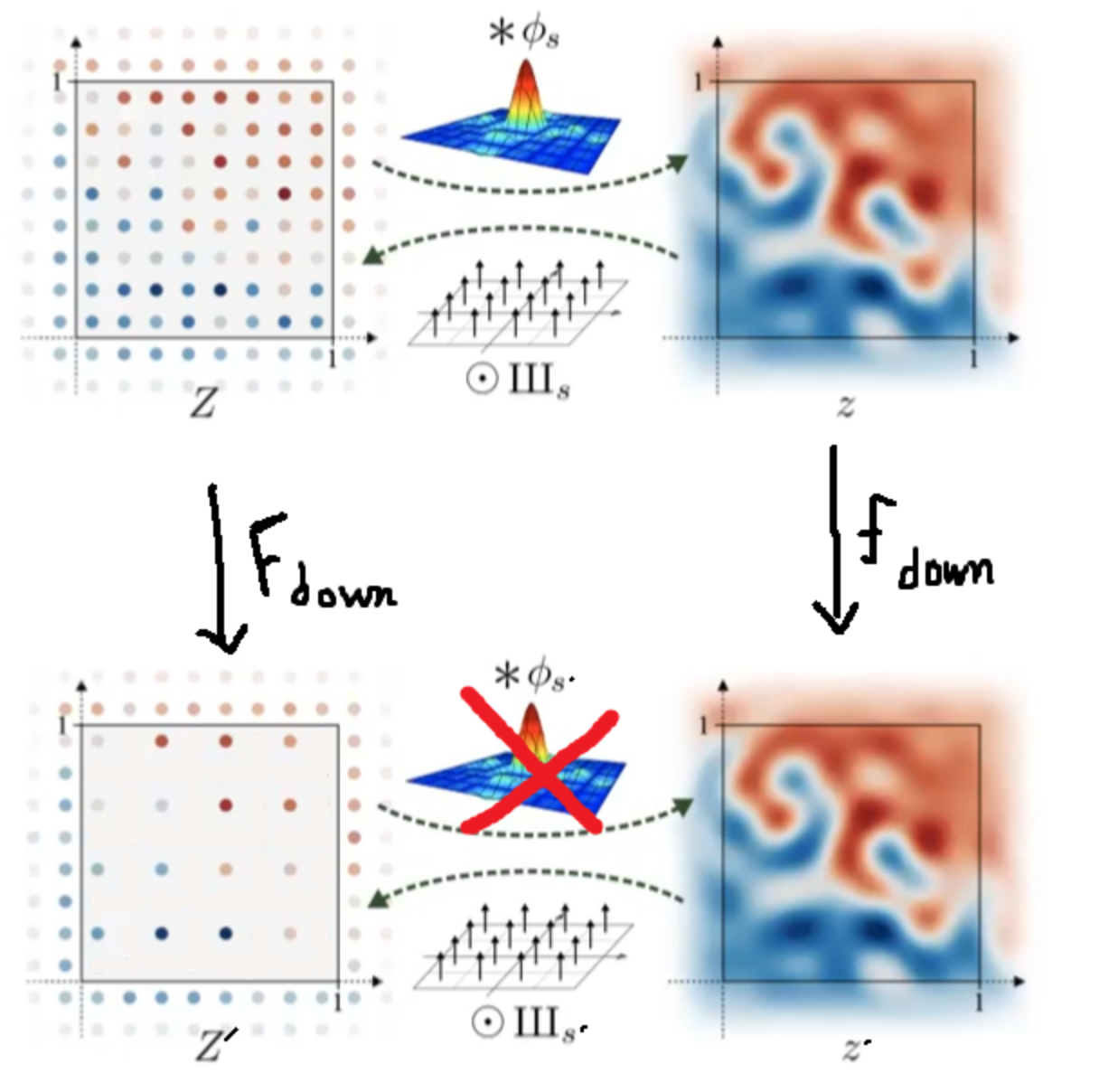
Downsampling

• 업샘플링과 비슷하지만 다른점은 sampling rate를 떨어트린다
  -> 대역폭 제한이 낮아져 제한보다 높은 주파수를 가지고 있는 연속 표현에서의 정보를 이산 표현으로부터 복원해 낼 수 없다
  

• 연속 표현의 주파수를 낮추기 위해서는 다운샘플링 후 재설계한 LPF적용
  

Nonlinearity

• 활성화 함수 ReLU
• Nonlinearity는 point-wise 연산이기 때문에 위치가 이동하였다고 해서 값이 달라지지 않는다.
  -> 하지만 공간이 극단적으로 바뀌기 때문에 임의의 높은 주파수가 주입 되었다고 본다

출처: https://ostin.tistory.com/53