벡터

벡터란

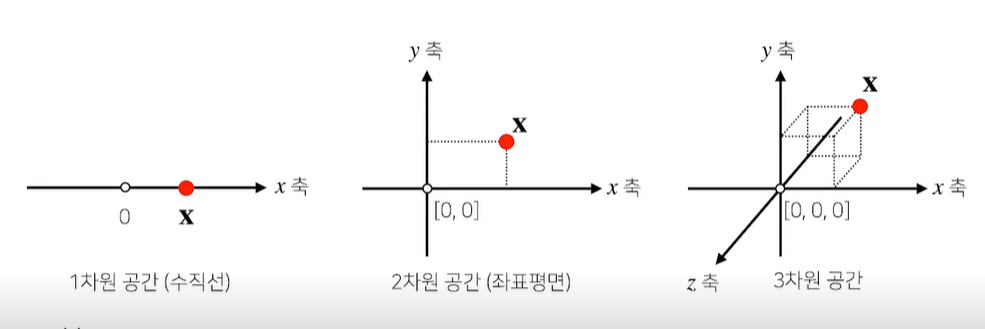
• 공간에서 한 점을 나타낸다

• 벡터는 원점으로부터 상대적 위치를 표현

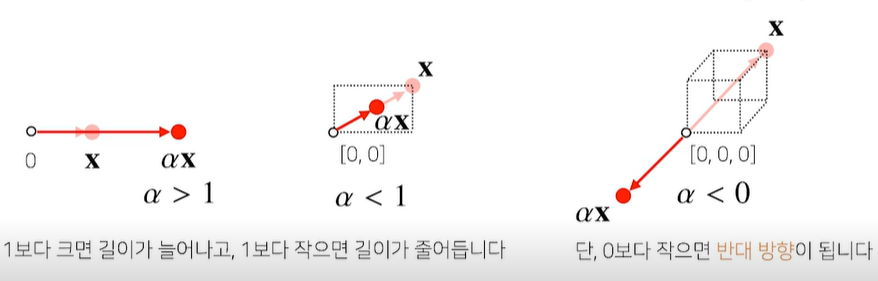
• 벡터에 숫자를 곱해주면 길이만 변한다. (스칼라 곱)
• 1보다 크면 늘어나고 작으면 줄어든다. 단, 0보다 작으면 반대 방향이다

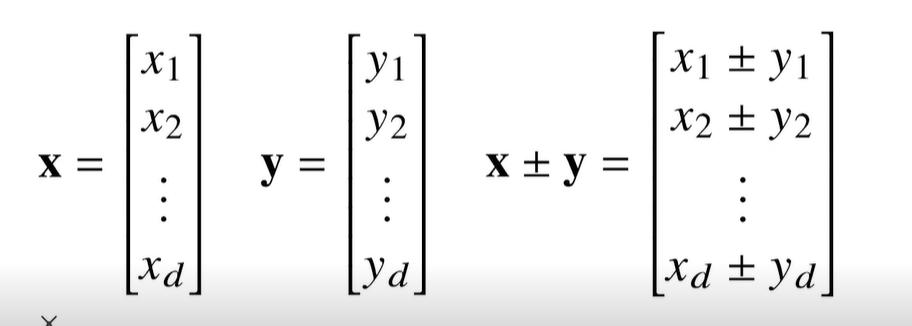
• 벡터는 숫자를 원소로 가지는 리스트 또는 배열
• 벡터끼리 같은 모양을 가지면 덧셈, 뺄셈을 계산 가능
• 벡터끼리 같은 모양을 가지면 성분곱 가능

벡터 덧셈, 뺄셈

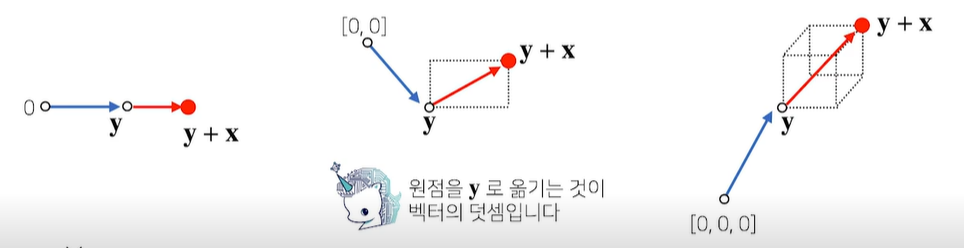
• 두 벡터의 덧셈은 다른 벡터로부터 상대적 위치이동을 표현

벡터 노름

• 원점에서부터의 거리를 뜻한다
• 벡터 노름은 임의의 차원d로 한다
• L1 노름은 각 성분의 변화량의 절대값을 모두 더한다
• L2 노름은 피타고라스 정리를 이용해 유클리드 거리 계산

# L1
def L1_norm(x) :
	x_norm = np.abs(x)
    x_norm = np.sum(x_norm)
    return x_norm

#L2
def L2_norm(x) :
	x_norm = x*x
    x_norm = sum(x_norm)
    x_norm = np.sqrt(x_norm)
    return x_norm

왜 다른 노름을 소개하는가

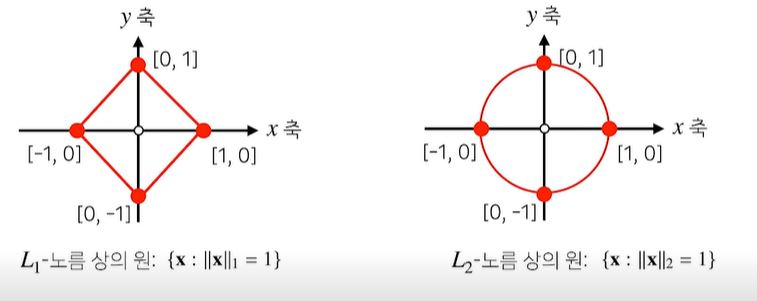
-> 머신러닝에선 각 성질들이 필요할 때가 있으므로 둘 다 사용

• 노름의 종류에 따라 기하학적 성질이 달라진다.
• L1은 마름모 형식처럼 나옴(lasso)
• L2은 원 같이 나옴(릿지, 라플라스)

두 벡터 사이의 거리를 구한다

• L1과 L2를 이용하면 두 벡터 사이의 거리를 계산할 수 있다.
  

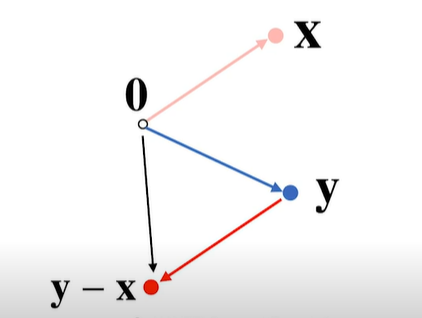
• 두 벡터 사이의 거리를 계산할 때는 벡터의 뺄셈을 이용

두 벡터 사이의 각도 구한다

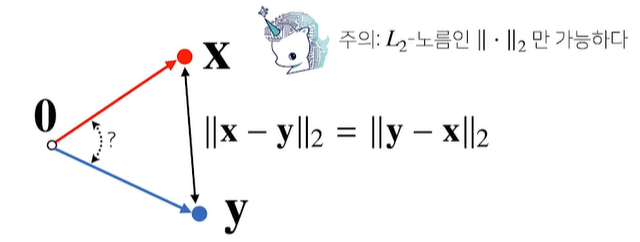
• 두 벡터 사이의 거리를 이용하여 각도도 구할 수 있다. 단, L2노름에서만 가능
• inner함수를 활용하여 판단 가능

def angle(x, y):
	v = np.inner(x,y) / (l2_norm(x) * l2_norm(y))
    theta = np.arccos(v)
    return theta

내적이란

• 정사영된 벡터의 길이와 관련 있다
• Proj(x)의 길이는 코사인법칙에 의해 된다.
  
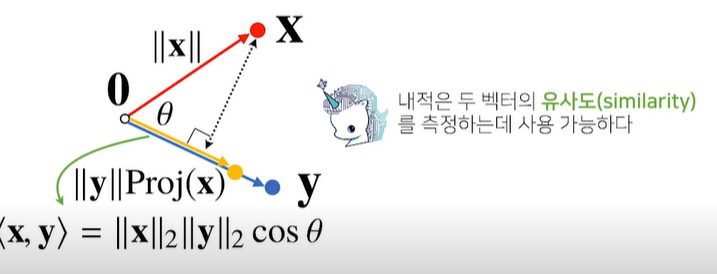
• 내적은 정사영의 길이를 벡터 y의 길이 ||y||만큼 조정한 값이다.
  -> 내적은 두 벡터의 유사도를 측정하는데 사용 가능

*출처 https://www.boostcourse.org/ai100/lecture/739176?isDesc=false