행렬이란

• 벡터는 숫자를 가지는 1차원 배열
• 행렬은 벡터를 원소로 가지는 2차원 배열이다.
  
• 행렬은 행과 열이라는 인덱스를 가집니다.
• 행렬의 특정 행(열)을 고정하면 행(열)벡터라 부릅니다

전체행렬

• 행과 열의 인덱스가 바뀐 행렬'

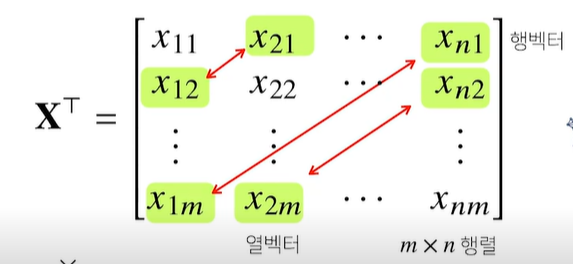
행렬을 이해하는 방법(1)

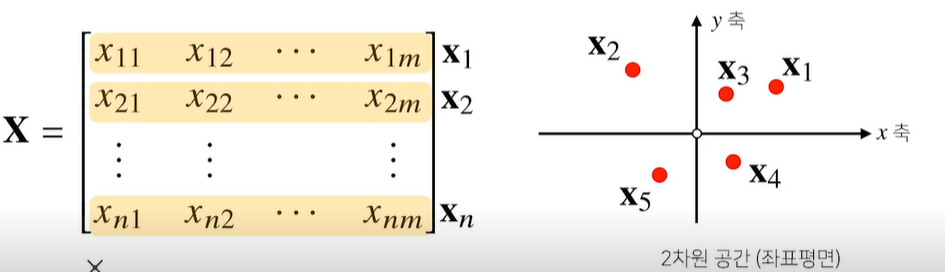
• 벡터가 공간에서 한 점을 의미한다면 행렬은 여러 점들을 나타낸다
• 행렬의 핵벡터xj는 i번째 데이터를 의미
• 행렬 xij는 i번째 데이터의 j번째 변수의 값
• 행렬은 벡터를 원소로 가지는 2차원 배열
• 같은 모양을 가지면 덧셈, 뺄셈, 성분곱 가능

행렬곱셈

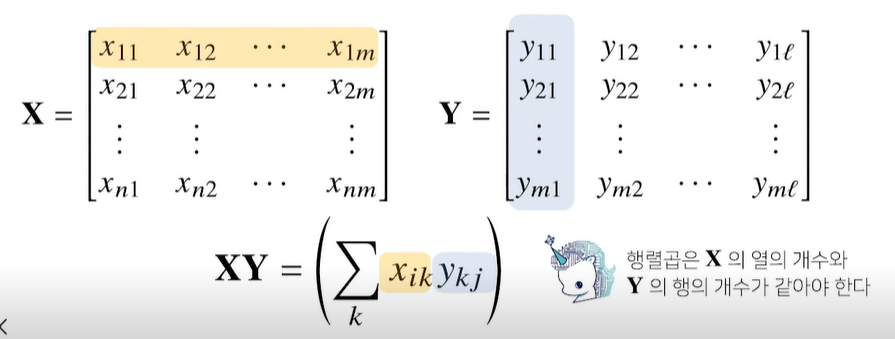
• i번째 행벡터와 j번째 열벡터 사이의 내적을 성분으로 가지는 행렬을 계산

행렬의 내적

• 주의!!
  • 행렬의 곱셈은 i의 행벡터와 j의 열벡터를 계산(x의 열과 y의 행의 개수가 같아야함)
  • 행렬의 내적은 i와 j의 행벡터 사이의 내적을 계산(수학에서의 내적과 다름 numpy의 np.inner)

행렬을 이해하는 방법(2)

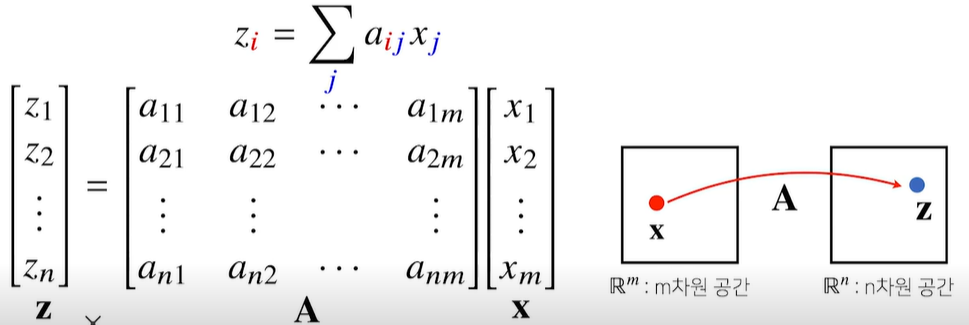
• 벡터공간에서 사용되는 연산자로 이해한다
• 행렬곱을 통해 벡터를 다른 차원의 공간으로 보낼 수 있다.
• A와 X를 곱하면 z라는 새로운 벡터 공간이 만들어진다
  • 행렬곱을 통해 패턴을 추출할 수 있고 데이터를 압축할 수도 있다

역행렬 이해하기

• 어떤 행렬 A의 연산을 거꾸로 되돌리는 행렬를 뜻함. 역행렬은 행과 열 숫자가 같고 행렬식이 0이 아닌 경우에만 계산할 수 있다.

np.linalg.inv(x)를 통해 역행렬 구할 수 있다

• 역행렬을 계산하기 위해서는 행과 열의 숫자가 같아야한다

• 만일 역행렬을 계산할 수 없다면 유사역행렬 또는 무어펜로즈 역행렬A+을 활용

np.linalg.pinv()

응용1:연립방정식 풀기

응용2: 선형회귀분석

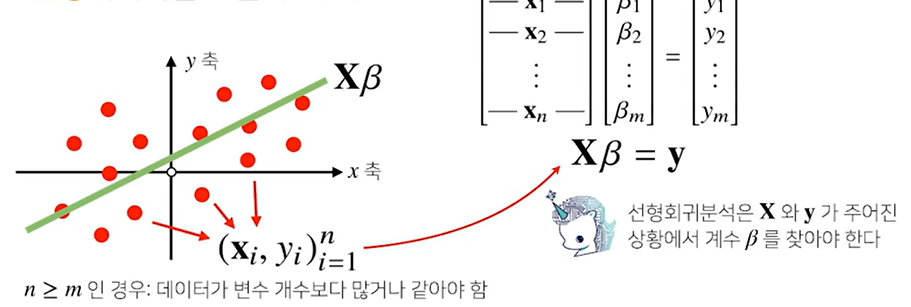
• np.linalg.pinv를 이용하면 데이터를 선형모델로 해석하는 선형회귀식 찾을 수 있다.
• 어떤 b를 사용해야 빨간 점을 잘 표현하는가가 선형회귀식이다

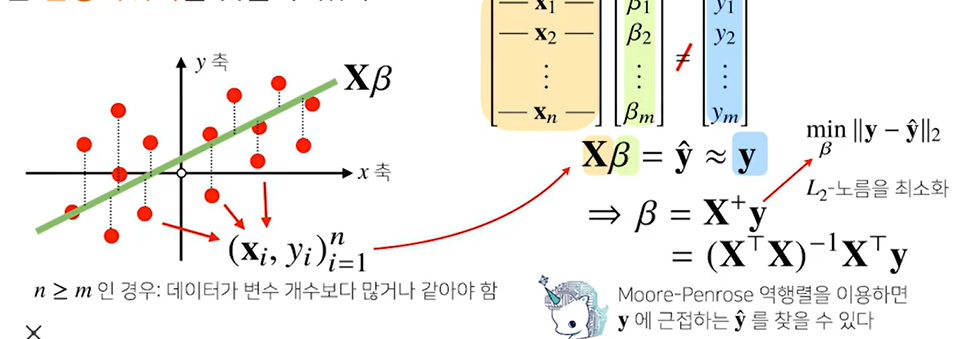
• 예측한 y헷과 y가 최소화가 되는 점
• l2노름을 최소화하는 것을 찾는다
• 역행렬을 사용하면 y에서 l2노름에 가장 근접하는 y헷을 구할 수 있다

from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(x,y)
y_test = model.predict(x_test)

# y절편을 추가해줘야한다
x_ = np.array([np.append(x,[1]) for x in x])
beta = np.linalg.pinv(x) @ y
y_test = np.append(x_test) @ beta