신경망과 로지스틱회귀

이진분류

• 로지스틱 회귀는 이진 분류를 위한 알고리즘이다.
• 이진분류는 그렇다(1) 아니다(0)표현한다

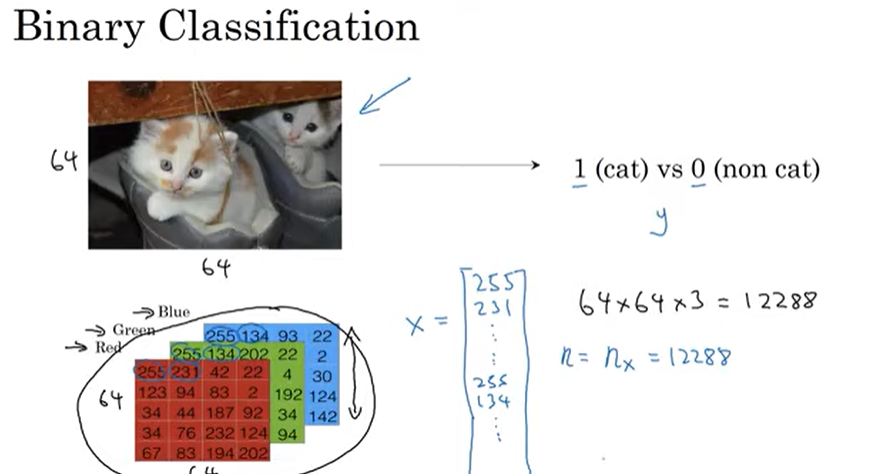
• 컴퓨터에 사진이 저장될 때 64 x 64라면 64의 빨초파의 픽셀 강도 값을 나타낸다
• 픽섹 강도 값들을 특성 벡터로 바꾸려면 한 열로 나열한다
  • 64 x 64의 빨초파의 특성벡터는 64 x 64 x 3이 된다
• 이진분류의 목표는 입력된 사진을 나타내는 특성 벡터x를 가지고 그에 대한 레이블 y가 1 또는 0 즉 고양이인지 고양이가 아닌지 예측하는 분류기 학습

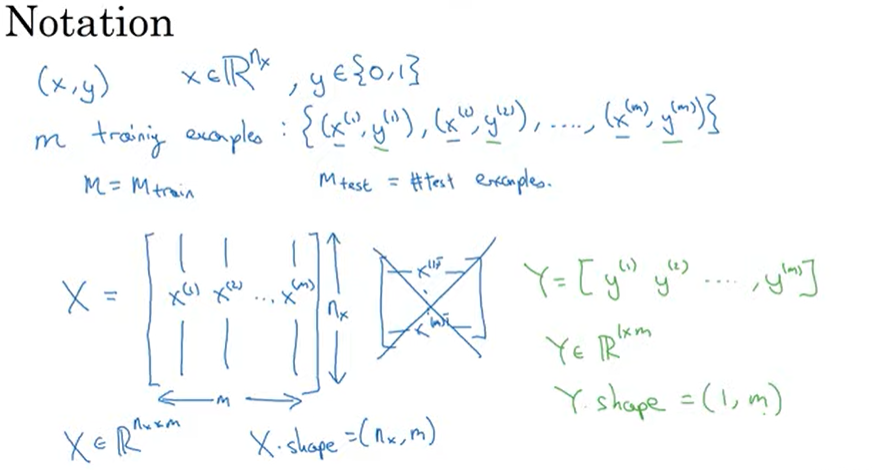
• 단 하나의 훈련 샘플을 한쌍(x,y)로 표시할 때
• x는 nx차원상의 특성 벡터, y레이블은 0또는 1이다
• m개의 훈련샘플 입력과 출력 표기
• m = mtrain, 테스트세트 개수 mtest
• 모든 훈련 샘플들을 간결하는 표기방법 행렬 x사용
• x.shape = (nx,m) nx,m행렬 뜻함, y.shape = (1,m)

로지스틱 회귀

• 입력 값인 x에 대해서, y(주어진 입력 특성 x에 해당되는 실제 값)가 1일 때 예측 값을 ŷ
• 예측 값 ŷ은 x일 때 y가 1인 확률 0<=ŷ<=1이다.
• ŷ=wX +b(w,b=파라미트,w=입력값, b=잔차)에서 0과 1사이를 벗어날 수 있기에 시그모이드 함수를 사용해 0과 1사이 값으로 변환
  

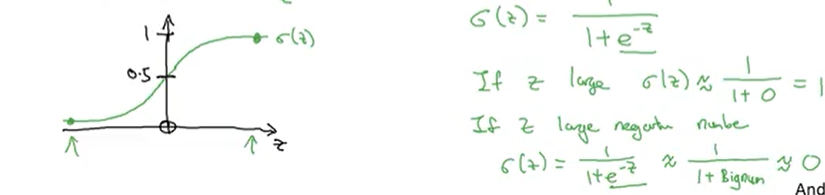
로지스틱 회귀의 비용함수

• 손실 함수는 하나의 입력에 대해 실제값(y)과 예측값(ŷ)의 차이인 오차를 계산하는 함수

• 모든 입력에 대한 오차를 계산하는 함수를 비용함수라 한다
  

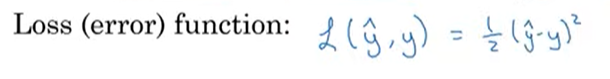
• 회귀 모형을 사용하는 목적은 실제값(y)과 근접한 예측값(ŷ)을 찾기를 위함이며, 비용함수의 값이 작아지도록 하는 w와 b를 찾는 것이 이를 위한 방법이다.

• 손실 함수

  • 출력된 y의 예측값과 참값 y사이에 오차가 얼마나 큰지를 측정
  • 
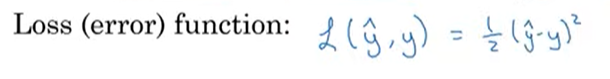
  • 로지스틱 회귀에서는 주로 사용하지 않는다. 매개변수들을 학습하기 위해 풀어야할 최적화 함수가 볼록? 하지 않기 때문-> 여러개의 지역 최적값을 가지고 있게 되어 문제가 생김(경사 하강범이 전역 최적값을 못 찾을 수도 있다)

로지스틱 회귀에서의 로스함수

• 
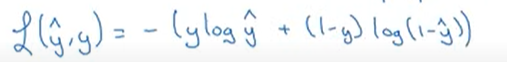
• 제곱 오차를 쓴다하면 그 오차를 최소화하려 할 것이다
• 손실함수는 훈련 샘플 하나에 관하여 정의돼서 그 하나가 얼마나 잘 예측 되었는지 측정

사용이유

• y가 1일 경우 로스함수는 -logy예측값이 된다
  • 
  • y예측값은 시그모이드 함수값이기 때문에 1보다 클 수 없으므로 1에 수렴하길 원한다
• y가 0일 경우 로스함수는 -log(1-y예측값)이 된다
  • 
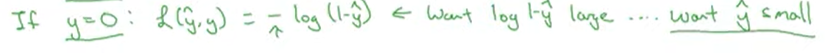
  • 학습 중에 손실함수값을 줄이고 싶다면 마이너스가 있기에 최대한 커져야한다 y의 예측값이 최대한 작아야한다 0과1사이기에 y예측값이 0에 수렴하도록 매개 변수들을 조정

요약

• 로지스틱 회귀 모델 학습이란 것은 손실함수j를 최소화해주는 매개변수들 w와b를 찾는것

경사하강법

• 비용함수가 전체 데이터셋의 예측이 얼마나 잘 되었는지 확인하는 것이면, 경사하강법은 이를 가능하게 하는 파라미터 w와 b를 찾아내는 방법이다
• 경사하강법 찾으려면 비용함수의 형태가 볼록한 형태여야 한다.
• 함수의 최솟값을 모르기 때문에 임의의 점을 시작으로 도함수, 함수의 기울기를 따라서 비용함수의 최저점을 찾아가는 과정

• 매개변수 w,b가 훈련 세트 전체를 얼마나 잘 예측하는지 비용함수를 통해 확인
• w,b를 찾기 위해서는 비용함수 J(w,b)를 가장 작게 만드는 w,b를 찾아야한다
  
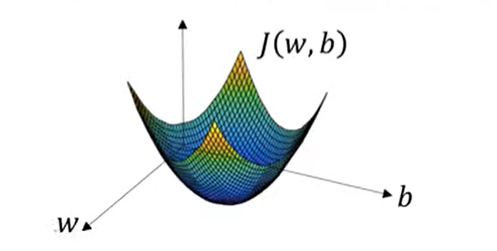
• 두 가로축은 w,b의 공간을 나타낸다 높이는 J(w,b)값을 나타낸다
  
• 비용함수 J는 활처럼 볼록한 함수 , 볼록하지 않은 함수는 지역 최적값 여러개
• 비용함수J(w,b)가 볼록하다는 사실이 로지스틱회귀에 비용함수J를 사용하는 이유다
• 매개변수로 쓸 좋은값을 찾기 위해서는 w,b를 어떤 초깃값으로 초기화해야한다
  • 보통 초깃값을 0으로 설정(무작위 초기화도 가능하지만 로지스틱 회귀에서는 사용x)
  • 위에 함수는 볼록하기에 어디서 초기화 해도 거의 같은점에 도착
  • 
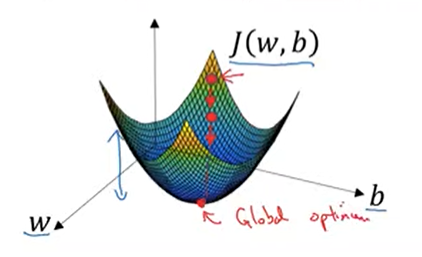
  • 경사하강법에 의해 내려오다가 전역최적값이나 근사치에 도달한다

예시(경사하강법에 의한 J함수)

• 
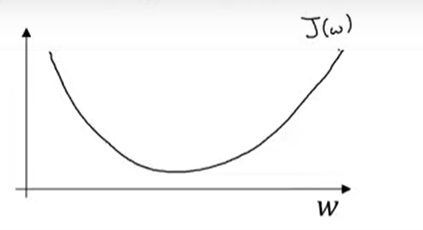
  • w값을 수렴할때까지 업데이트한다
  • a는 학습률을 뜻함
  • 미분계수는 w에 줄 변화를 뜻함(기울기) 통상적으로 dw라고 적는다

• 도함수(dw)가 0보다 크면, 파라미터 w는 기존의 w보다 작은 방향으로 이동하고, 반면 dw가 0보다 작으면 w는 기존의 w보다 큰 방향으로 이동 반복하면 최저점 찾게됨
• 즉 왼쪽에서 초기화 하던 오른쪽에서 초기화 하던 경사하강법은 매개변수를 전역 최솟값까지 도달하게 한다

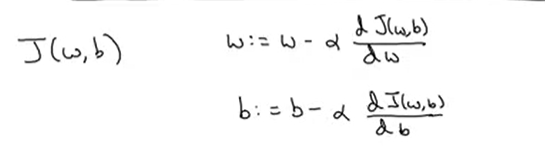
• 비용함수는 J(w,b)두개의 매개변수이므로 위와 같은 식으로 사용한다

도함수

• 도함수는 함수의 기울기와 동일하며, 높이/너비로 구한다. 일차 이차 로그함수 등 함수에 따라 도함수의 값은 다르지만, 축의 값이 증가, 감소함에 상관없이 도함수의 값은 일정
  

• a가 2일때, 0.0001만큼 오른쪽으로 이동하는 경우에 도함수는 4이다

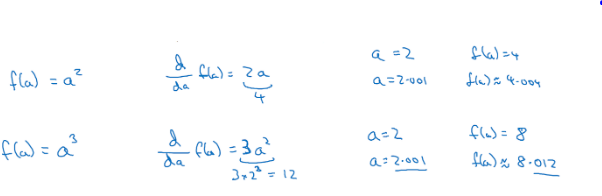
• 이차함수와 삼차함수 경우에도 동일 축 변화 상관없이 도함수는 동일

계산그래프

신경망의 계산은

• 정방향 패스, 정방향 전파는 신경망의 출력값을 계산
• 역방향 패스, 역방향 전파로 이어져 경사나 도함수를 계산한다

계산그래프를 사용하는 경우

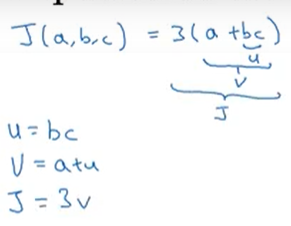
• 함수를 계산할 때 서로 다른 세단계의 과정이 필요
• 먼저 bc를 계산 이를 u라는 변수에 저장 u=bc
• v=a+u로
• 출력값 J=3v

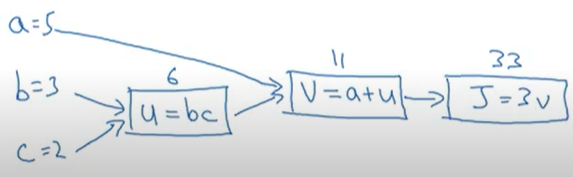
• 위는 a,b,c를 각각 5,3,2대입 했을 경우
• 계산 그래프는 J같은 특정한 출력값 변수를 최적화 하고 싶을 때 사용
• 로지스틱 회귀의 경우 J는 최적화할 비용 함수이다
• 계산그래프는 왼쪽에서 오른쪽의 패스로 J값을 계산할 수 있다는 것

계산그래프 미분

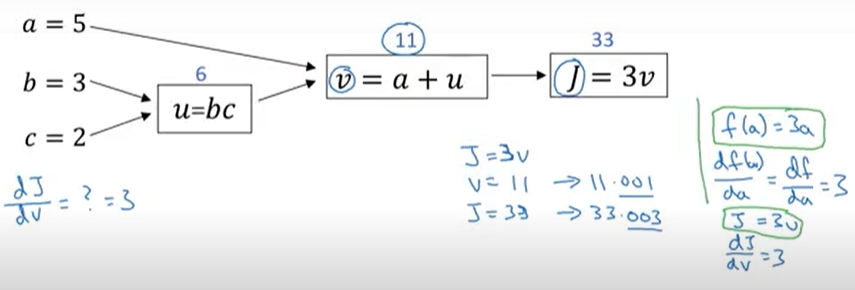
• v값을 아주 조금 바꾸면 J값이 어떻게 바뀌는지

• 역전파 마지막 출력값 변수의 v에 대한 도함수를 얻으면
  

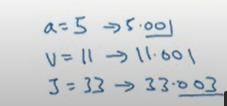
• a의 새로운 값을 넣었을 때 a의 변화가 계산 그래프의 오른쪽으로 전파되어 J가 33.003이 된다는 뜻

• J의 증가량은 a의 증가량보다 3배 많고 이는 도함수 3을 뜻함

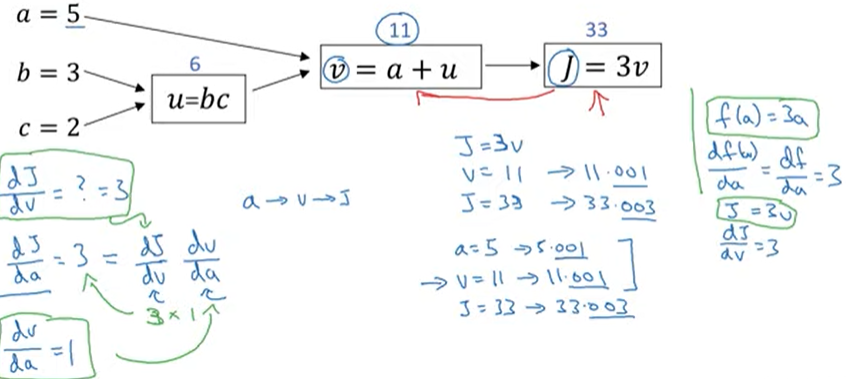
• dj/dv를 계산하는 것이 dj/da를 계산하는데 도움을 줄 수 있다
• 이와 같은 것이 역방향 계산의 한단계중 하나

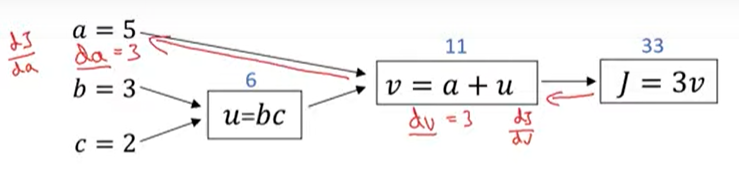
• dv는 dj/dv를 나타내는 변수
• da는 dj/da를 나타내는 변수
• dj/du =3 , du =3
  • u = 6->6.001, v = 11->11.001, j = 33->33.003 증가시켜본다
• 도함수를 계산할 때 가장 효율적인 방법으로 하려면 정방향과 역방향 계산하는 방법
• 정방향 계산으로 최적화 하고자 하는 J같은 비용함수를 계산하는 것과 역방향 계산으로 도함수를 계산

로지스틱 회귀의 경사하강법

로지스틱 회귀의 경사하강법을 위해 필요한 핵심 공식을 구현하는 방법
여기서는 계산그래프를 통해 구현 계산 그래프를 로지스틱 회귀의 경사 하강법에 사용하는 것은 조금 과할 수 있다 -> 완전한 신경망을 다룰 때 이해가 더 쉬울 것이다.

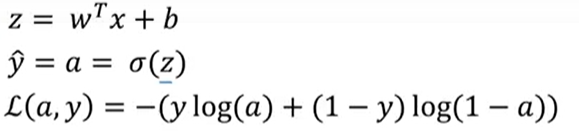
• 로지스틱 회귀에서 목적은 매개변수 w와b를 변경해서 L(a,y)의 손실을 줄이는 것

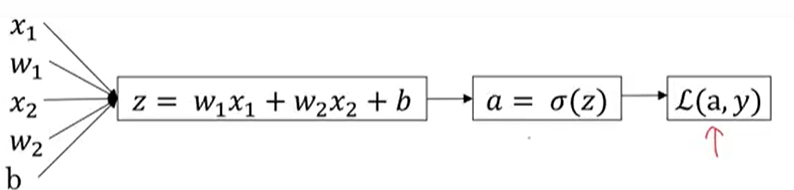
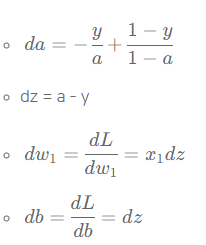
• 위 손실함수의 도함수를 구하려고 하니 역방향으로 가서 a에 대한 손실함수의 도함수를 계산한다 연쇄법칙을 이용해서 도함수를 위와 같이 구할 수 있다
• 단일 샘플에 대한 경사하강법 한단계이다 도함수를 계산하고 단일 샘플에 대한 로지스틱 회귀의 경사 하강법을 구현하는 방법이다. 실제로는 m개의 훈련 샘플을 가진 훈련 세트를 훈련해야한다

m개 샘플의 경사하강법

• 비용함수J 표현