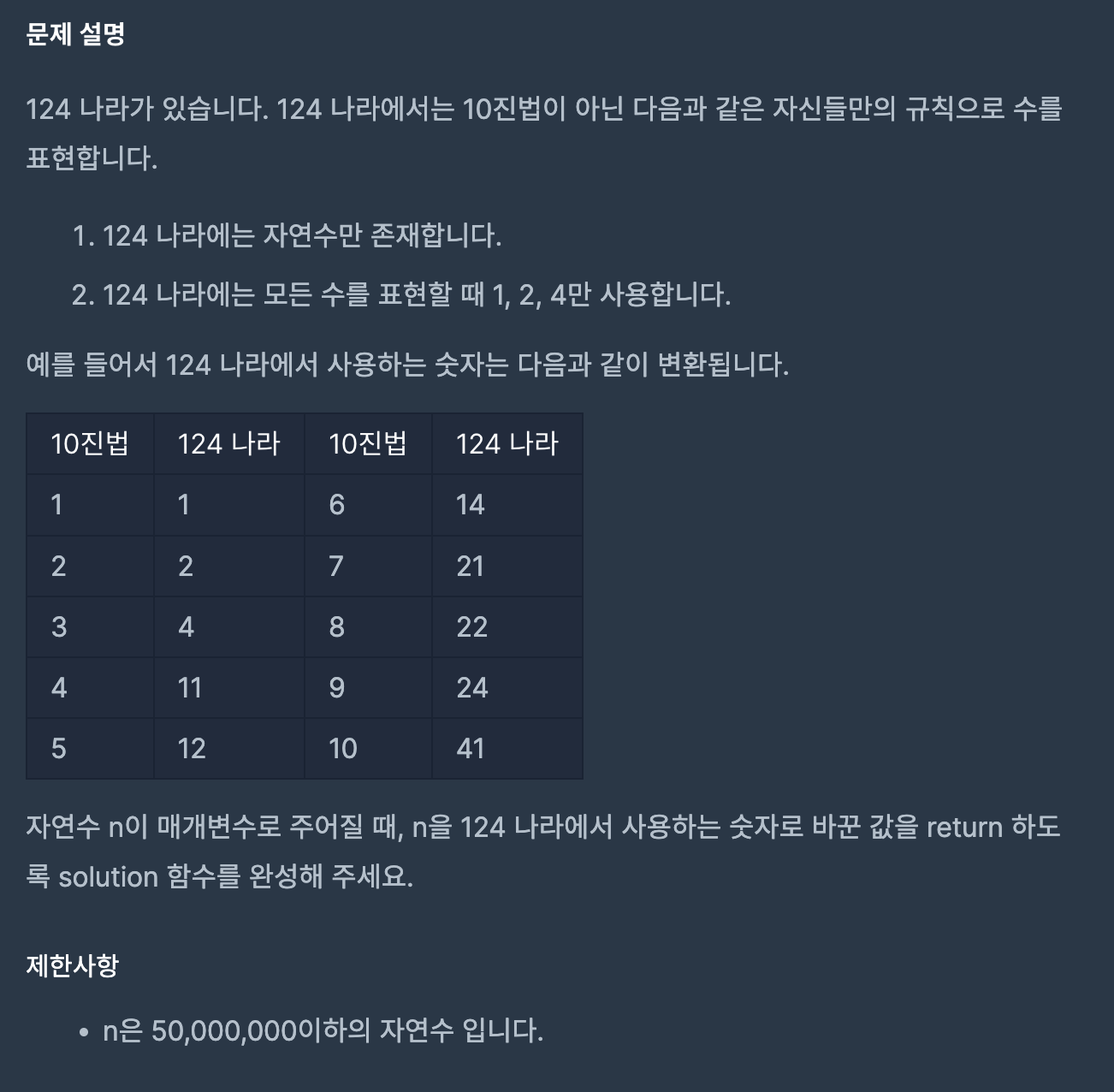
문제

문제 바로가기

풀이

첫 번째 풀이

18의 경우까지 손으로 직접 확인해보다가, 규칙을 찾아서 적용했다.

1번째 발견 규칙
숫자 n에 대해서, 124숫자의 마지막 수는

• n%3 == 0이면 4로 끝난다.
• n%3 == 1이면 1로 끝난다.
• n%3 == 2이면 2로 끝난다.

2번째 발견 규칙
숫자 n에 대해서, 124숫자의 마지막 수를 제외한 앞 글자는

• (n-1)/3의 숫자와 같다.

코드

class Solution {
  long[] memo;
  static int[] suffix = {4, 1, 2};
  public String solution(int n) {
    memo = new long[n<3 ? 4 : n+1];
    memo[1] = 1;
    memo[2] = 2;
    memo[3] = 4;
    
    return String.valueOf(dp(n));
  }
  public long dp(int num) {
    if(memo[num]!=0) {
      return memo[num];
    }
    memo[num] = dp((num-1)/3)*10+suffix[num%3];
    return memo[num];
  }
}

그런데 효율성 테스트에서 시간 초과가 뜬다. 흠

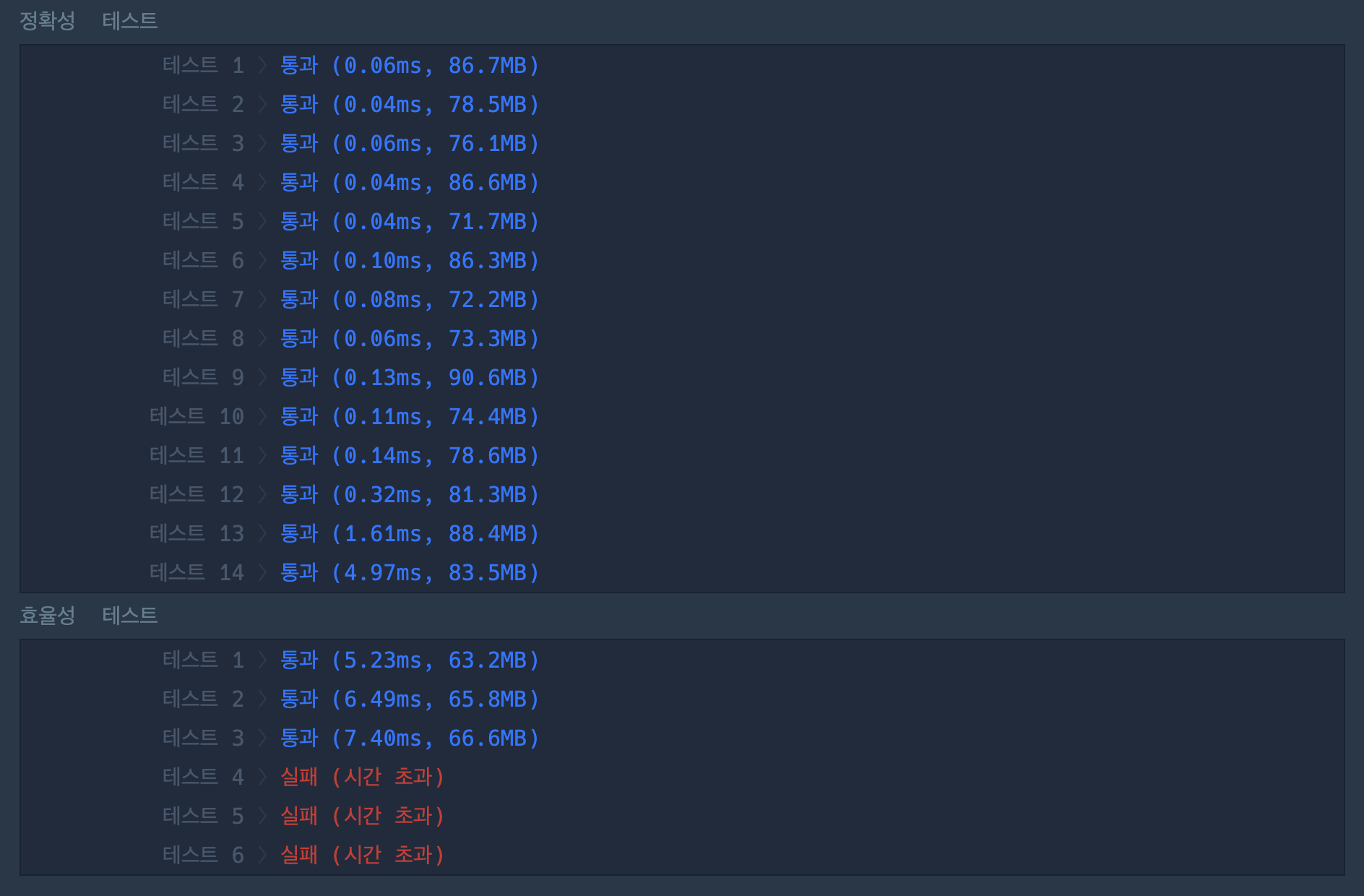
발생할 수 있는 최악의 케이스?

• n으로 주어질 수 있는 최대 정수 : 50000000
• 이 경우 dp() 메서드를 15번 호출한다.
• 15번이면 괜찮은거 아녀...?! 왜 시간초과가 뜨는거지?

해결, 최종 풀이

내 논리가 틀린 것 같지는 않고, 뭐가 문젠지 모르겠어서 채찍피티한테 물어봤더니 반복문을 사용해서 효율을 높여보라고 조언을 해줬다.
그래서 반복문을 사용했더니 확실히 시간복잡도도 줄고, 효율성 테스트를 통과 할 수 있었다.

코드

class Solution {
  static int[] suffix = {4, 1, 2};
    
  public String solution(int n) {
    StringBuilder sb = new StringBuilder();
    while(n>0) {
        sb.append(suffix[n%3]);
        n = (n-1)/3;
    }     
    return sb.reverse().toString();
  }
}

---

결론

재귀가 반복문보다 공간복잡도가 높고 성능이 떨어질 수 있다는 건 그냥 익히 알고 있는 사실이었지만, 실제 문제 풀이에 적용할 생각을 바로 떠올리지 못 했다는 것이 놀랍다.

재귀 함수를 통해 푸는 것이 논리적으로 편해서 항상 반복문보다는 재귀를 더 선호했던 것 같다.
그래도 이 문제를 계기로 재귀 함수를 짜기 전 또는 후, 반복문으로 더 간단히 풀 수 있는지 확인해볼 수 있을 것 같다!