[이코테] 이진 탐색 - 공유기 설치

🔔 문제

도현이의 집 N개가 수직선 위에 있습니다. 각각의 집의 좌표는 x1, x2, ..., xn이고 집 여러 개가 같은 좌표를 가지는 일은 없습니다.

도현이는 언제 어디서나 와이파이를 즐기기 위해서 집에 공유기 C개를 설치하려고 합니다. 최대한 많은 곳에서 와이파이를 사용하려고 하기 때문에, 한 집에서는 공유기를 하나만 설치할 수 있고, 가장 인접한 두 공유기 사이의 거리를 가능한 크게하여 설치하려고 합니다.

C개의 공유기를 N개의 집에 적당히 설치해서, 가장 인접한 두 공유기 사이의 거리를 최대로 하는 프로그램을 작성하세요.

입력

• 첫째 줄에 집의 개수 N (2<=N<=200,000)과 공유기의 개수 C (2<=C<=N)가 하나 이상의 빈칸을 사이에 두고 주어집니다.
• 둘째 줄부터 N개의 줄에는 집의 좌표를 나타내는 xi (1<=xi<=1,000,000,000)가 한 줄에 하나씩 주어집니다.

출력

• 첫째 줄에 가장 인접한 두 공유기 사이의 최대 거리를 출력합니다.

🎯 풀이방법

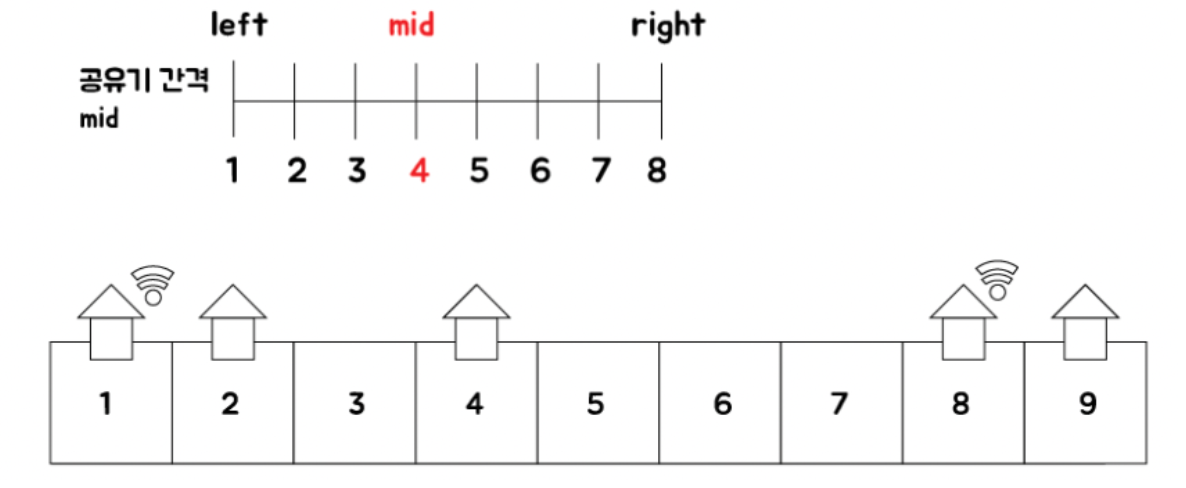
이 문제는 '가장 인접한 두 공유기 사이의 거리'의 최댓값을 탐색해야 하는 문제로 이해할 수 있다. 이때 각 집의 좌표가 최대 10억이므로, 이진 탐색을 이용하면 문제를 해결할 수 있다. 따라서 이진 탐색으로 '가장 인접한 두 공유기 사이의 거리'를 조절해가며, 매 순간 실제로 공유기를 설치하여 c보다 많은 개수로 공유기를 설치할 수 있는지 체크하여 문제를 해결할 수 있다. 다만, '가장 인접한 두 공유기 사이의 거리'의 최댓값을 찾아야 하므로, c보다 많은 개수로 공유기를 설치할 수 있다면 '가장 인접한 두 공유기 사이의 거리'의 값을 증가시켜서, 더 큰 값에 대해서도 성립하는지 체크하기 위해 다시 탐색을 수행한다.

💻 python code

n, c = map(int, input().split())

array = []
for _ in range(n):
    array.append(int(input()))
array.sort()

start = 1
end = array[-1] - array[0] # 집의 좌표 중에 가장 큰 값
result = 0

while(start <= end):
    mid = (start + end) // 2 # mid는 가장 인접한 두 공유기 사이의 거리(gap)를 의미
    value = array[0]
    count = 1
	
    # 현재의 mid값을 이용해 공유기를 설치
    for i in range(1, n):
        if array[i] >= value + mid:
            value = array[i]
            count += 1
    if count >= c: # c개 이상의 공유기를 설치할 수 있는 경우, 거리를 증가
        start = mid + 1
        result = mid
    else: # c개 이상의 공유기를 설치할 수 없는 경우, 거리를 감소
        end = mid - 1

print(result)