문제 설명
고고학자인 "튜브"는 고대 유적지에서 보물과 유적이 가득할 것으로 추정되는 비밀의 문을 발견하였습니다. 그런데 문을 열려고 살펴보니 특이한 형태의 자물쇠로 잠겨 있었고 문 앞에는 특이한 형태의 열쇠와 함께 자물쇠를 푸는 방법에 대해 다음과 같이 설명해 주는 종이가 발견되었습니다.
잠겨있는 자물쇠는 격자 한 칸의 크기가 1 x 1인 N x N 크기의 정사각 격자 형태이고 특이한 모양의 열쇠는 M x M 크기인 정사각 격자 형태로 되어 있습니다.
자물쇠에는 홈이 파여 있고 열쇠 또한 홈과 돌기 부분이 있습니다. 열쇠는 회전과 이동이 가능하며 열쇠의 돌기 부분을 자물쇠의 홈 부분에 딱 맞게 채우면 자물쇠가 열리게 되는 구조입니다. 자물쇠 영역을 벗어난 부분에 있는 열쇠의 홈과 돌기는 자물쇠를 여는 데 영향을 주지 않지만, 자물쇠 영역 내에서는 열쇠의 돌기 부분과 자물쇠의 홈 부분이 정확히 일치해야 하며 열쇠의 돌기와 자물쇠의 돌기가 만나서는 안됩니다. 또한 자물쇠의 모든 홈을 채워 비어있는 곳이 없어야 자물쇠를 열 수 있습니다.
열쇠를 나타내는 2차원 배열 key와 자물쇠를 나타내는 2차원 배열 lock이 매개변수로 주어질 때, 열쇠로 자물쇠를 열수 있으면 true를, 열 수 없으면 false를 return 하도록 solution 함수를 완성해주세요.
제한사항
key는 M x M(3 ≤ M ≤ 20, M은 자연수)크기 2차원 배열입니다.
lock은 N x N(3 ≤ N ≤ 20, N은 자연수)크기 2차원 배열입니다.
M은 항상 N 이하입니다.
key와 lock의 원소는 0 또는 1로 이루어져 있습니다.
0은 홈 부분, 1은 돌기 부분을 나타냅니다.
풀이
처음엔 이 문제를 보고 BFS로 접근하였다. 기존 BFS처럼 4방향 이동 + 회전으로 탐색하는 방식을 생각했지만, 탈출 조건을 만들 수 없어 이 풀이는 아니라는 것을 알았다.
그러다 못풀겠다 싶어 포기할라던 찰나, 정답률을 봤더니 40%... 오기가 생겨서 다시 마음을 다 잡고 풀어보았다.
그러다 생각해낸 풀이는, 결국 자물쇠에서 실제로 홈이 파져있는 영역을 잡고, 그 영역의 크기만큼 을 key에서 봤을 때, key가 자물쇠의 해당 영역의 반전된 값으로 이루어져 있으면 된다는 것이다.
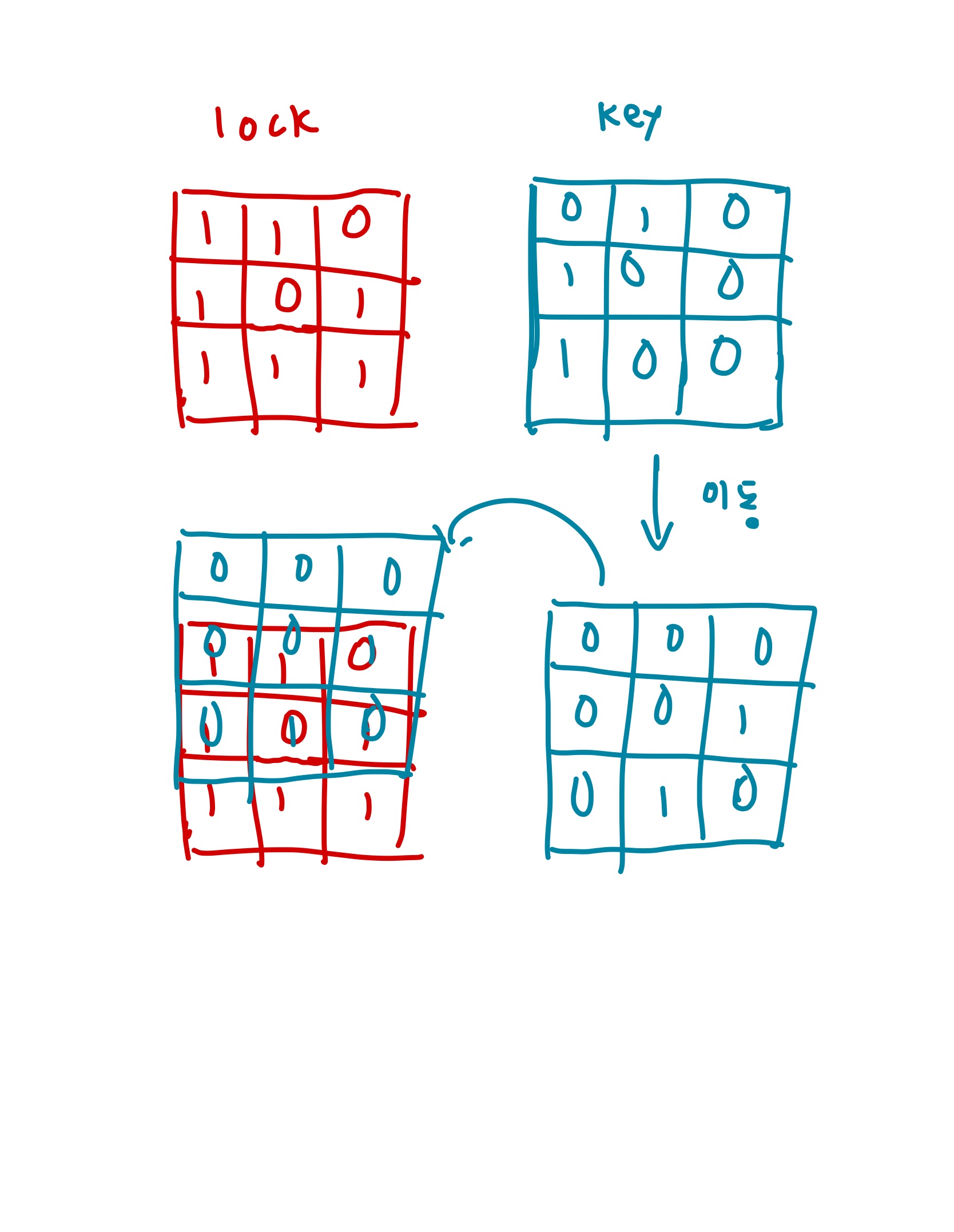
예를 들어 문제에서 준 예제를 보면 자물쇠의 홈이 파여져있는 영역은 (1,1) ~ (2,2)이다.
그러면 이제 key에서 2*2영역을 모두 보면서 해당 영역이 자물쇠의 (1,1)~(2,2)영역과 완전히 반전되어 있는 영역이 있다면 true를 리턴한다. 왜냐하면 결국 key의 해당 2*2영역외에는 모두
없앨 수 있기 때문이다. 이 부분이 헷갈릴 수 있는데 아래와 같은 과정을 거쳐 나머지 영역은 무시할 수 있다.
만약 그런 영역이 없다면 key를 오른쪽(왼쪽)으로 회전시킨 후 다시 반복한다.
2차원 배열을 오른쪽을 회전시키는 방법은 나는 아랫면이 왼쪽면이 되도록 한다. 3*3배열이면 (2,0) -> (1,0) -> (0,0) -> (2,1) -> (1,1) -> (1,0) -> (2,2) -> (1,2) -> (0,2) 이 순으로 읽으면서 새로운 배열의 왼쪽 위에서부터 차례대로 채워나간다.(r,c)
예외 케이스 힌트(드래그)
lock이 모두 돌기로만 이루어져 있는 경우.
정답 코드
class Solution {
int M;
int N;
public boolean solution(int[][] key, int[][] lock) {
boolean answer = false;
M = key.length;
N = lock.length;
int startR = -1;
int lastR = -1;
int startC = -1;
int lastC = -1;
for (int r=0; r<N; r++) {
for (int c=0; c<N; c++) {
if (startR == -1 && lock[r][c] == 0) {
startR = r;
lastR = r;
break;
} else if (lock[r][c] == 0) {
lastR = r;
break;
}
}
}
for (int c=0; c<N; c++) {
for (int r=0; r<N; r++) {
if (startC == -1 && lock[r][c] == 0) {
startC = c;
lastC = c;
break;
} else if (lock[r][c] == 0) {
lastC = c;
break;
}
}
}
int y = startR >= 0 ? lastR - startR + 1 : 0;
int x = startC >= 0 ? lastC - startC + 1 : 0;
int rotateCnt = 0;
while (rotateCnt < 4) {
for (int sr=0; sr<=M-y; sr++) {
for (int sc=0; sc<=M-x; sc++) {
boolean flag = true;
for (int r=0; r<y; r++) {
for (int c=0; c<x; c++) {
if (key[sr+r][sc+c] + lock[startR+r][startC+c] != 1){
flag = false;
break;
}
}
if (!flag) {
break;
}
}
if (flag) {
return true;
}
}
}
key = rotateKey(key);
rotateCnt ++;
}
return answer;
}
public int[][] rotateKey(int[][] key) {
int[][] newKey = new int[M][M];
int nr = 0;
int nc = 0;
for (int c=0; c<M; c++) {
for (int r=M-1; r>=0; r--) {
newKey[nr][nc] = key[r][c];
nc++;
}
nr++;
nc = 0;
}
return newKey;
}
}