[알고리즘 문제풀이]
1.[백준-14002번] 가장 긴 증가하는 부분 수열4

수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오.예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이고, 길이는 4이다.
2.[백준-1904] 01타일

지원이에게 2진 수열을 가르쳐 주기 위해, 지원이 아버지는 그에게 타일들을 선물해주셨다. 그리고 이 각각의 타일들은 0 또는 1이 쓰여 있는 낱장의 타일들이다.어느 날 짓궂은 동주가 지원이의 공부를 방해하기 위해 0이 쓰여진 낱장의 타일들을 붙여서 한 쌍으로 이루어진
3.[백준-1463] 1로 만들기

정수 X에 사용할 수 있는 연산은 다음과 같이 세 가지 이다.X가 3으로 나누어 떨어지면, 3으로 나눈다.X가 2로 나누어 떨어지면, 2로 나눈다.1을 뺀다.정수 N이 주어졌을 때, 위와 같은 연산 세 개를 적절히 사용해서 1을 만들려고 한다. 연산을 사용하는 횟수의
4.[백준-11726] 2 x n 타일링

2×n 크기의 직사각형을 1×2, 2×1 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오.아래 그림은 2×5 크기의 직사각형을 채운 한 가지 방법의 예이다.첫째 줄에 n이 주어진다. (1 ≤ n ≤ 1,000)첫째 줄에 2×n 크기의 직사각형을 채우는 방법의 수
5.[백준-11727] 2 x n 타일링 2

2×n 직사각형을 1×2, 2×1과 2×2 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오.아래 그림은 2×17 직사각형을 채운 한가지 예이다.첫째 줄에 n이 주어진다. (1 ≤ n ≤ 1,000)첫째 줄에 2×n 크기의 직사각형을 채우는 방법의 수를 10,00
6.[백준-9095] 1,2,3 더하기

정수 4를 1, 2, 3의 합으로 나타내는 방법은 총 7가지가 있다. 합을 나타낼 때는 수를 1개 이상 사용해야 한다.첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, 정수 n이 주어진다. n은 양수이며 11보다 작다.각 테스
7.[백준-11052] 카드 구매하기
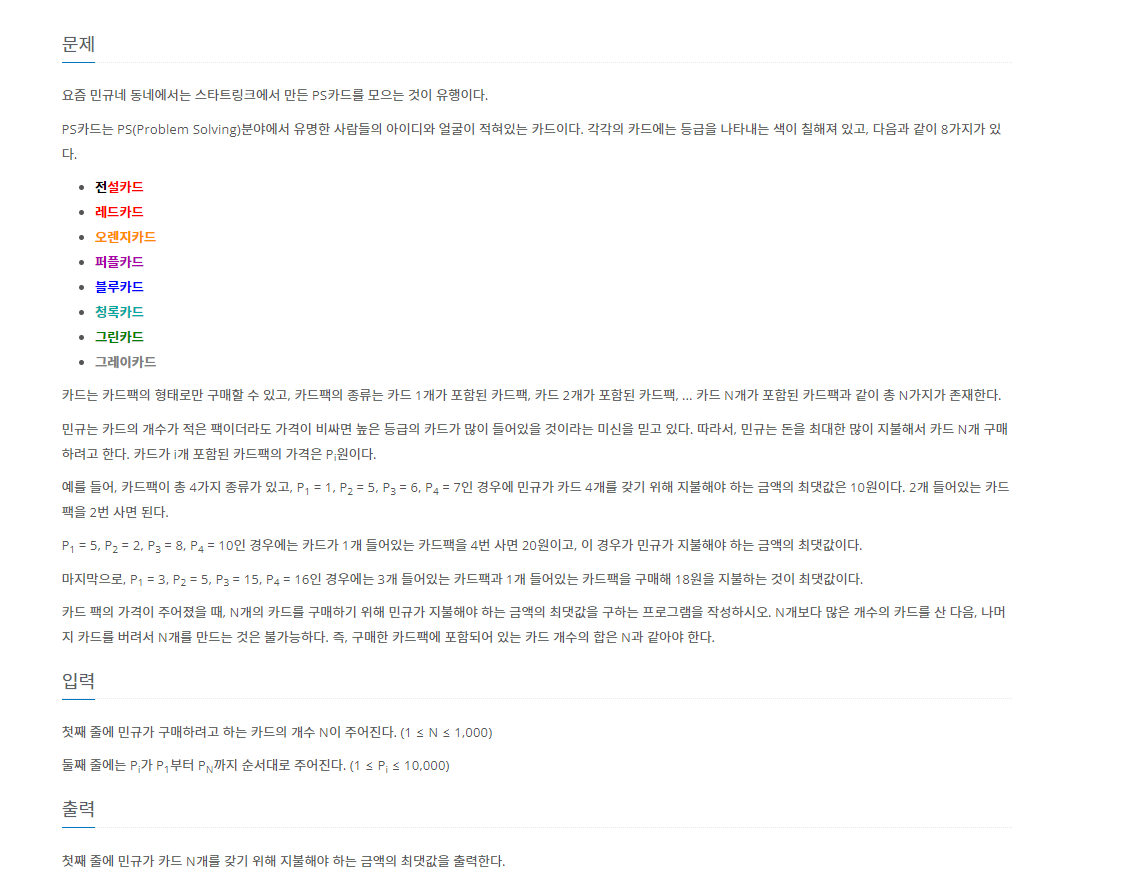
다이나믹 프로그래밍을 통해서 풀었다.dp2는 2개카드 1개, 혹은 1개카드 2개 중 더 비싼값이다.dp3는 3개카드 1개, 혹은 1,dp2 중 더 비싼값이다. 이는 1,1,1로 3을 만드는 경우, 1,2로 3을 만드는 경우 둘다 처리가 dp2에서 처리가 된다.dpi는
8.[백준-16194] 카드 구매하기2

다이나믹 프로그래밍을 통해서 문제를 풀었다.dpi는 i개의 카드를 구매할 때 금액의 최소값이다.따라서 dpi=min(pi,dp1+dpi-1,dp2+dpi-2....) 이다.
9.[백준-15990] 1,2,3 더하기5

dpi는 정수i를 1,2,3들의 합으로 만들때 맨끝이 1,2,3인 경수의 개수를 저장하는 리스트이다. 예를 들어 정수4는 1+2+1, 1+3, 3+1로 1로 끝나는 경우 2개, 2로 끝나는 경우 0개, 3으로 끝나는 경우 1개만들수있다. 따라서 dp4는 2,0,1의 값
10.[백준-2193] 이친수

dpi에는 i자리 이친수를 0으로 끝나는 이친수의 수,1로 끝나는 이친수의 수 형태로 저장한다.i자리 이친수 중 0으로 끝나는 이친수의 수는 i-1자리 이친수 중 0으로 끝나는 이친수 + i-1자리 이친수 중 1로 끝나는 이친수 이다.1로 끝나는 이친수의 수는 i-1자
11.[백준-1699] 제곱수의 합

처음에는 그리디 알로리즘으로 풀었는데 n=12일때 틀린 답이 나왔다. 그래서 다이나믹 알고리즘으로 풀었다.j\*j는 i보다 같거나 작은 제곱수로, j\*j가 i를 제곱수의 합으로 나타내는 항들중 가장 큰 값인 경우에 항의 수중 가장 작은 값이 dpi값이 된다. i가 제
12.[백준-14501] 퇴사

graph에는 t,p가 들어간다.dp는 n번째날에서 첫번째날로 거꾸로 되돌아가면서 탐색한다.dpi는 i번째날의 상담을 포함하면서 n번째날까지 포함가능한 상담중 최대 수익을 저장한다.max(dp\[graphi+i:])는 i번째날상담의 끝나는 다음날부터 마지막날까지의 수익
13.[백준-2225] 합분해

k=4일때 n의 값을 1부터 올려보면1일때는 (0,0,0,1),(0,0,1,0),(0,1,0,0),(1,0,0,0)로 총4개이다2일때는 1일때 경우들에 (0,0,0,1),(0,0,1,0),(0,1,0,0),(1,0,0,0)을 각각 더해준 경우로 4+3+2+1=10개이다
14.[백준-15988] 1,2,3 더하기 3

n은 (n-3을 만드는 구성)+3 , (n-2를 만드는 구성)+2, (n-1을 만드는 구성)+1으로 만들수 있다.따라서 dpn=dpn-3+dpn-2+dpn-1 이다.
15.[백준-1309] 동물원

dp1~dp3까지 구해다 보니 dp3=2\*dp2+dp1 인것을 발견하여 점화식 dpi=2\*dpi-1+dpi-2을 세워 풀어봤더니 맞았다.2\*i의 우리에 사자를 넣는 경우의 수는 (2\*(i-1)의 우리에 사자를 넣는 경우 중 맨위2개의 우리중 하나엔 사자가 있는
16.[백준-11057] 오르막 수
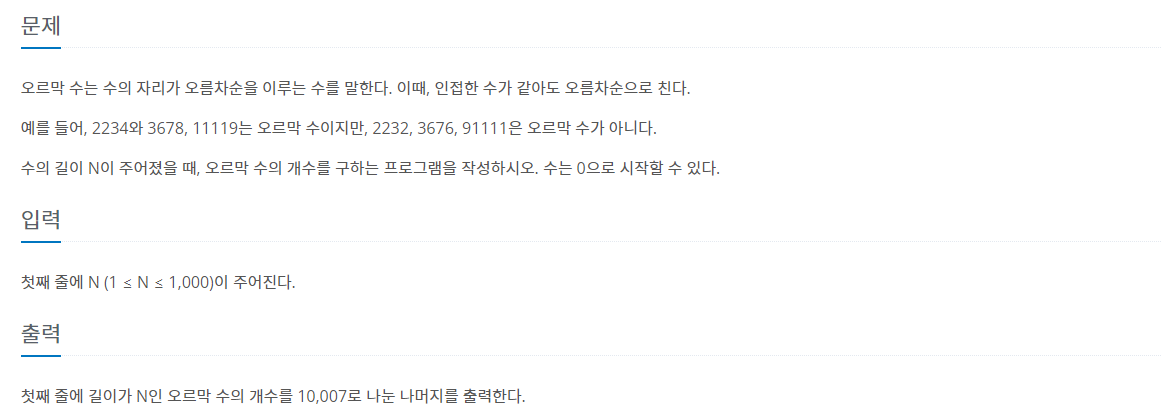
dpi는 i자리수 중 j로 시작하는 오르막수의 개수이다. 이는 i-1번째 오르막 수 중에서 첫째자리가 j와같거나 j보다 큰 수앞에 j를 추가하는 거와 같다.다른 사람들 풀이는 dpi에 i자리 중 j값이 가장 끝에 오는 오르막 수의 개수가 들어간다. j값이 가장 끝에 올
17.[백준-11055] 가장 큰 증가 부분 수열
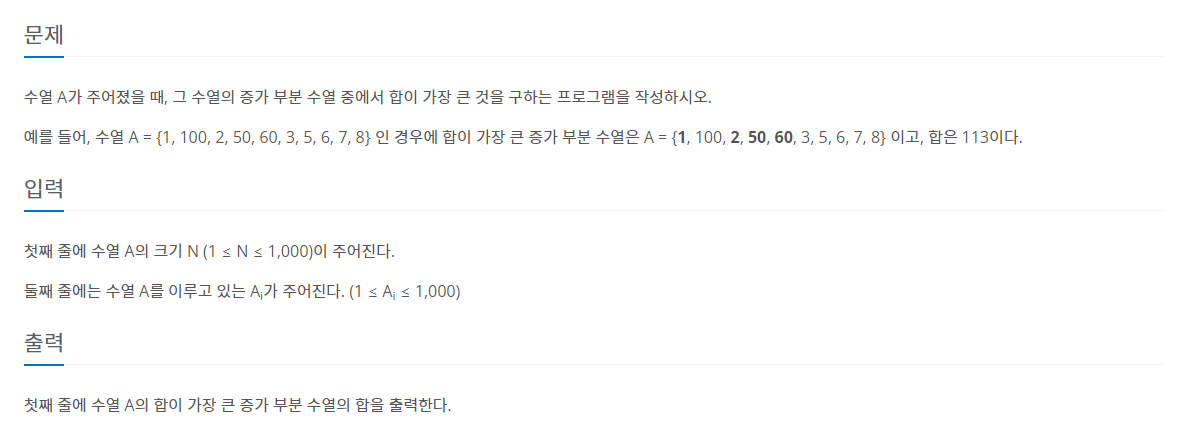
처음엔 dp를 수열의합, 수열의 가장큰수로 이중리스트로 관리하였지만 생각해보니 수열의 가장 큰수는 항상 해당 인덱스의 a값으로 필요가없다는걸 깨달았다. 그래서 일반리스트로 증가수열중 가장 큰값을 저장하도록 하였다.dpi는 dp0~dpi-1까지 값중 증가수열을 만족하
18.[백준-11722] 가장 긴 감소하는 부분 수열
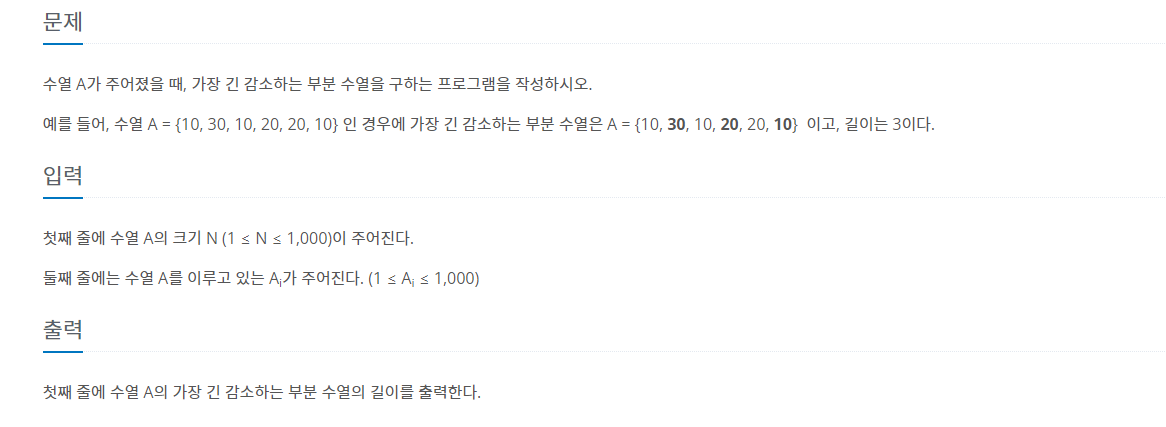
dpi엔 i까지 가장 긴 감소하는 부분 수열의 길이를 저장한다.이를 위해서 0번부터 i-1번까지의 감소부분수열을 만족하면서 가장 큰값에다가 +1한값이 dpi값이 된다.
19.[백준-13398] 연속합 2

생각해보다가 풀리지 않아 검색을 통해서 풀었다.dp0는 특정 원소를 제거하지 않은 경우dp1는 특정 원소를 제거한 경우어떠한 원소도 삭제하지않는 경우는 (이전까지의 연속합+i번째원소)와 (i번째 원소)중 큰값을 대입어떠한 원소를 삭제한 경우는 2가지로 나누어 생각한다.
20.[백준-11048] 이동하기
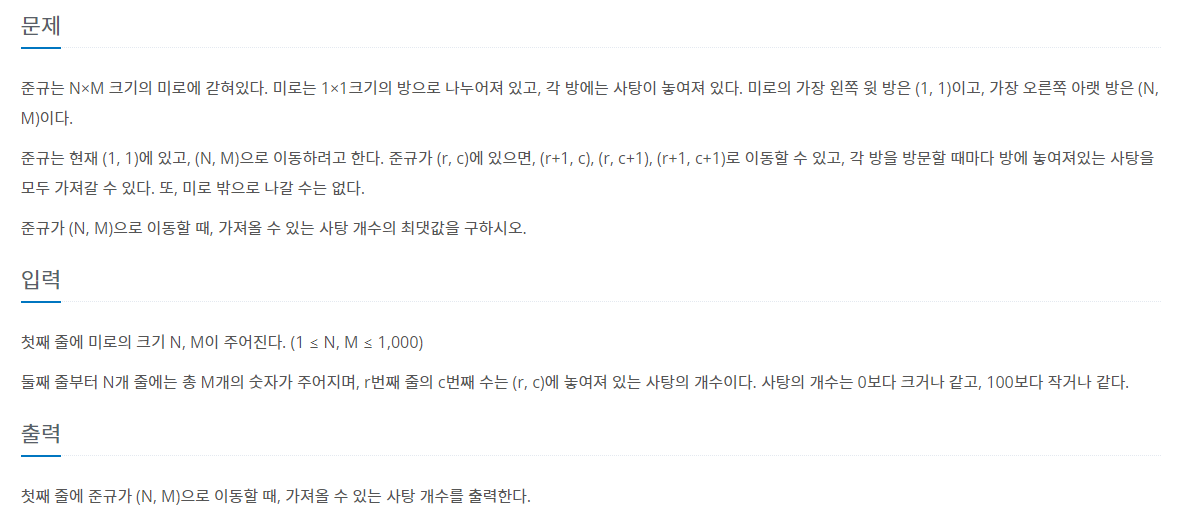
dpi에는 (i,j)미로방에 가지고들어갈 사탕의 최대 가수이다.이는 dpi-1+mazei-1 혹은 dpi+mazei-1 혹은 dpi-1+mazei-1 중 가장 큰 값이다.mazei-1인 이유는 dp의 크기가 n+1,m+1 이기 때문이다.
21.[백준-11060] 점프 점프
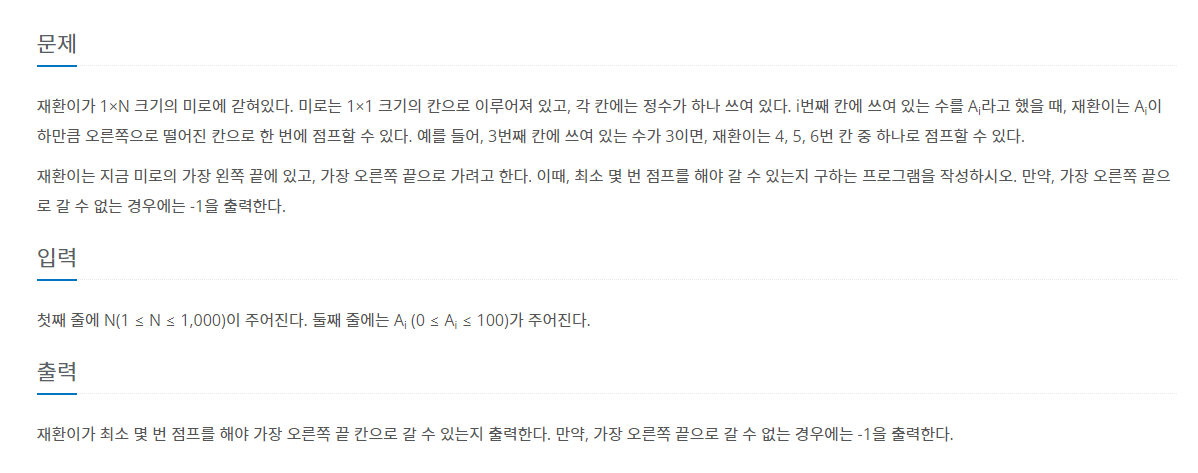
나는 맨 마지막부터 처음으로 돌아오면서 최소 점프 횟수를 구하는 방식으로 문제를 풀었다.예를 들어 입력이n=10maze=1 2 0 1 3 2 1 5 4 2이렇게 주어지면dp9는 9번방부터 9번방까지 최소 점프 횟수이므로 0이다.dp8은 8번방부터 9번방까지 최소 점프
22.[백준-11060] 점프 점프

나는 맨 마지막부터 처음으로 돌아오면서 최소 점프 횟수를 구하는 방식으로 문제를 풀었다.예를 들어 입력이n=10maze=1 2 0 1 3 2 1 5 4 2이렇게 주어지면dp9는 9번방부터 9번방까지 최소 점프 횟수이므로 0이다.dp8은 8번방부터 9번방까지 최소 점프
23.[백준-15989] 1,2,3 더하기 4
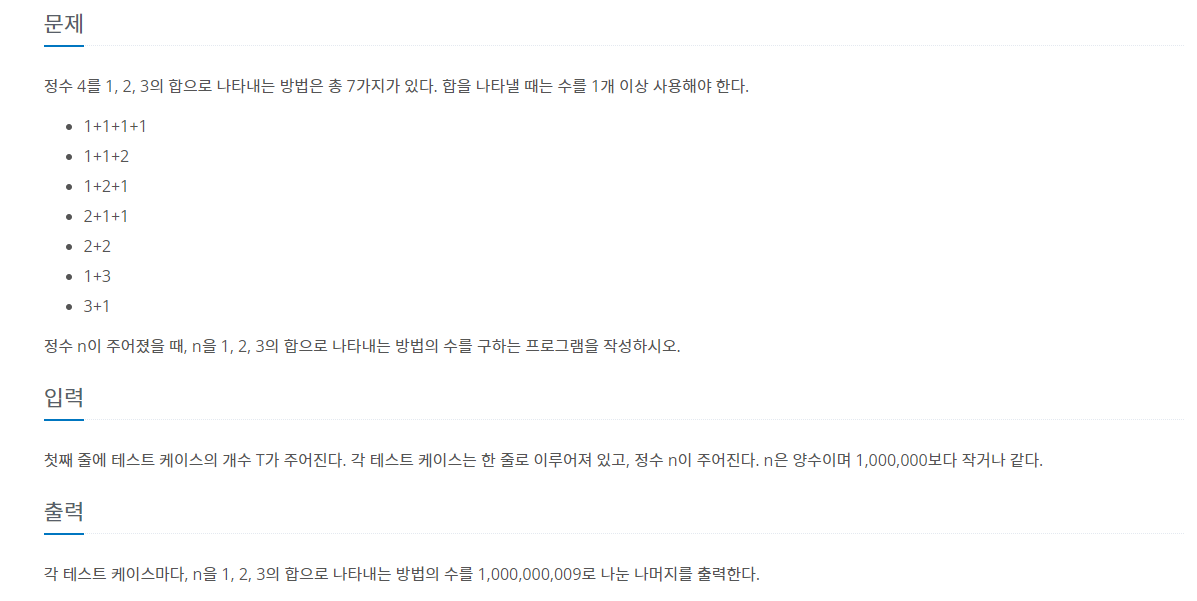
dp에는 정수i를 1,2,3의 합으로 나타내는 구성을 1이 가장 큰 구성, 2가 가장 큰 구성,3이 가장 큰 구성 로 저장한다.dpi의 1이 가장 큰 구성은 dpi-3의 1이 가장 큰 구성과 같다.dpi의 2가 가장 큰 구성은 dpi-2의 1이 가장 큰 구성과 2가
24.[백준-1495] 기타리스트

i번째 곡을 연주할 때 가능한 볼륨이 j라 할때 dpj=i이다.예를 들어 2(i)번째 곡을 연주할때 1(i-1)번째 곡을 연주할 때의 볼륨들인 dpj=1인 j값(볼륨)들을 찾고 그 j값에 volumes2(현재조절가능한볼륨)을 빼거나 더한값이 0이상 m이하이면 dp\[
25.[백준-2293] 동전 1
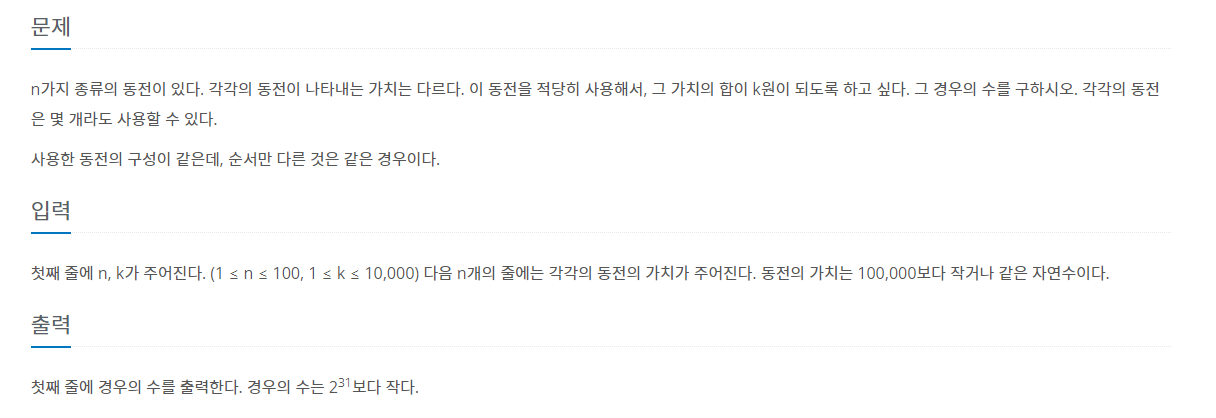
dpi에는 동전 가치의 합이 i인 경우의 수이다.입력받은 수를 c라고 할 때 i는 i-c의 경우들에 c를 그냥 더하면 되므로 dpi+=dpi-c가 된다.만약 동전의 가치가 1,2,5 이면 dp10=dp9+dp8+dp5 인데 문제에 구성은 같고 순서만 다른거는 같은 경우
26.[백준-2294] 동전 2
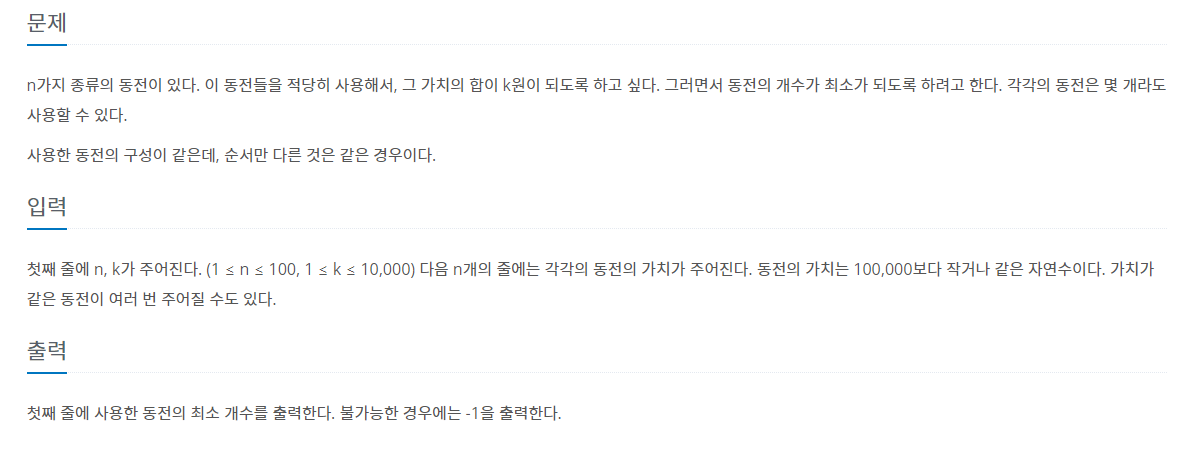
dpi는 현재까지 입력받은 가치들의 합으로 i를 만드는 경우의 수이다. 입력이 1이들어오면 1의 합으로 i를 만드는 경우의 수를 구하고 그 다음 입력으로 2가 들어오면 1과 2의 합으로 i를 만드는 경우의 수를 구한다. 그리고 순서는 구성의 상관이 없으므로 현재 입력받
27.[백준-11058] 크리보드
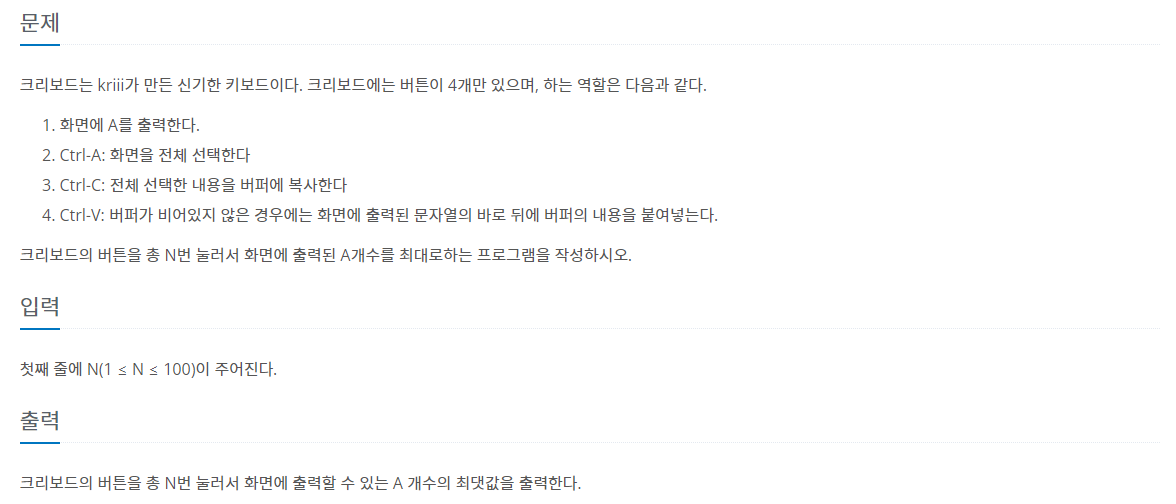
1~6까지는 그냥 A를출력하는 버튼을 그 숫자만큼 누르는게 복사해서 붙여넣기하는 것보다 더 많거나 같다.7부터는 무조건 붙여넣기 하는게 더 많아지고 붙여넣기를 1~3번한 것중 답이있다.(왜 1~3번중에 답이 있는지는 잘 모르겠다.)따라서 dpi=max(dpi-3\*2,
28.[백준-9251] LCS
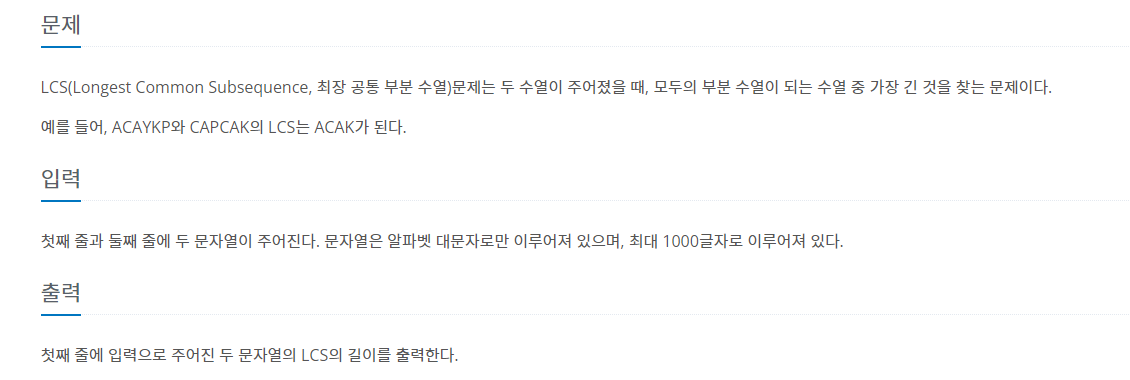
ACAYKP 와 CAPCAK 를 예시로 앞의 문장의 sub sequence를 a, 뒤에 문장의 sub sequence를 b라 하면a:Ab:CA두 문자열로 만들 수 있는 LCS의 길이: 1a:Ab:CA두 문자열로 만들 수 있는 LCS의 길이:1...위와 같이 b를 하나씩
29.[백준-5582] 공통 부분 문자열
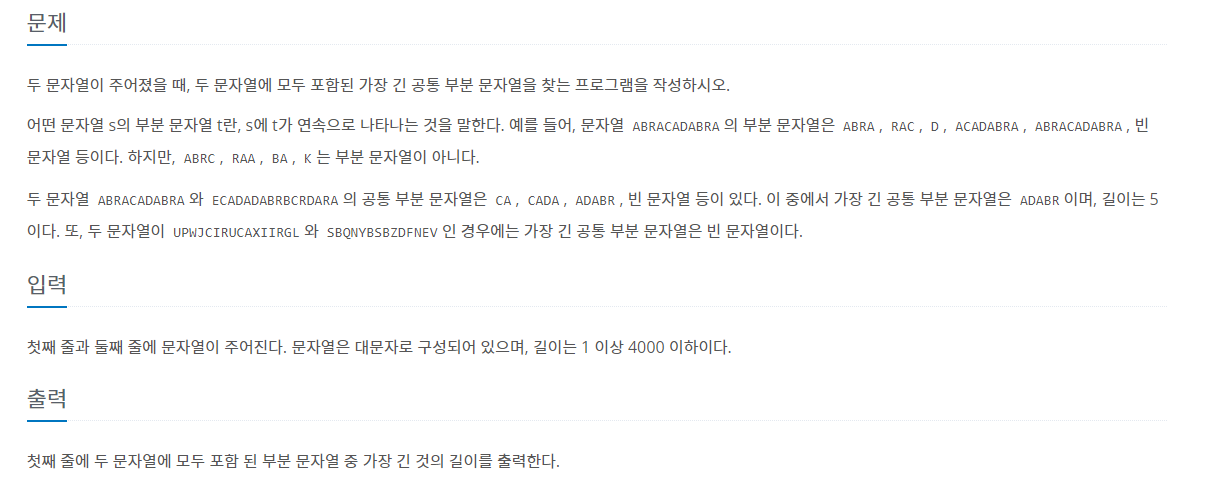
예시로 ABRACADABRA , ECADADABR에 대해서 생각해보자dp를 이중리스트로 선언하고 dp를 돌다가 같은 문자가 만나면 현재의 문자가 각 문자열의 이전문자와 연속되는 문자면 그 연쇡되는 문자의 개수에 +1을 해준다.dpi=dpi-1+1문자가 다르면 연속되지
30.[백준-5557] 1학년

나는 2개의 list를 이용해서 문제를 풀었다. 하나는 i인덱스 까지 계산했을 때 나오는 수들을 인덱스로 하여 값을 i로 하는 리스트이고 이를 dp라고 하겠다.예를 들어 2번인덱스 까지 계산한 값들이 1,4,5라면 dp1=2,dp4=2,dp5=2이다.그다음 3번인덱스까
31.[프로그래머스] 자물쇠와 열쇠 (LEVEL3)
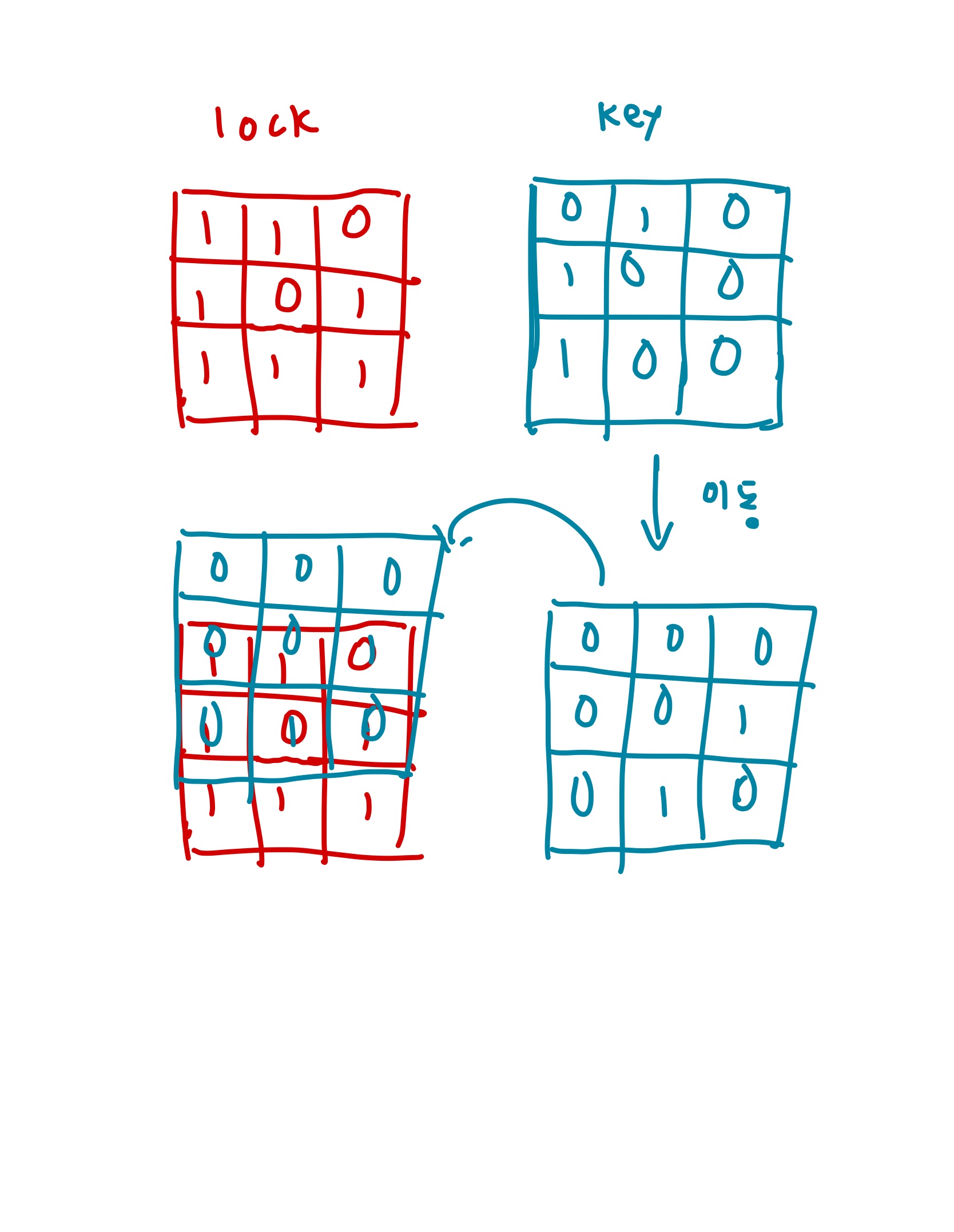
고고학자인 "튜브"는 고대 유적지에서 보물과 유적이 가득할 것으로 추정되는 비밀의 문을 발견하였습니다. 그런데 문을 열려고 살펴보니 특이한 형태의 자물쇠로 잠겨 있었고 문 앞에는 특이한 형태의 열쇠와 함께 자물쇠를 푸는 방법에 대해 다음과 같이 설명해 주는 종이가 발견
32.[프로그래머스] 주사위 고르기(Level3)

문제 설명 A와 B가 n개의 주사위를 가지고 승부를 합니다. 주사위의 6개 면에 각각 하나의 수가 쓰여 있으며, 주사위를 던졌을 때 각 면이 나올 확률은 동일합니다. 각 주사위는 1 ~ n의 번호를 가지고 있으며, 주사위에 쓰인 수의 구성은 모두 다릅니다. A가 먼