[알고리즘] 동적계획법(Dynamic Programming ;DP)

동적계획법 (Dynamic Programming ;DP)

• 하나의 큰 문제를 여러 개의 작은 문제로 나누고, 같은 문제라면 한 번씩만 풀어
  (그 결과를 저장하여 다시 큰 문제를 해결할 때 사용) 효율적으로 해결하는 알고리즘
• 큰 문제를 작은 문제로 쪼개서 그 답을 저장해두고 재활용! 기억하며 푸는 것!

사용 이유

• 일반적인 재귀 방식 또한 DP와 매우 유사
• 일반적인 재귀를 단순히 사용 시 동일한 작은 문제들이 여러 번 반복되어 비효율적 계산이 될 수 있음

방법

• 모든 작은 문제들은 한번만! 풀어야 함 따라서 정답을 구한 작은 문제를 어딘가에 메모해 둠
• 다시 그보다 큰 문제를 풀어나갈 때 똑같은 작은 문제가 나타나면 앞서 메모한 작은 문제의 결과값을 이용

조건

1. 작은 문제가 반복이 일어나는 경우
2. 같은 문제는 구할 때마다 정답이 같다

• 위 두가지 조건을 만족하는 경우 DP 사용 가능

Memoization 기법

• DP를 구현하는 방법 중 한 종류
• 한 번 구한 결과를 메모리 공간에 메모해두고 같은 식을 다시 호출하면 메모한 결과를 그대로 가져오는 기법
• 메모이제이션은 값을 저장하는 방법으로 캐싱(Caching)이라고도 함

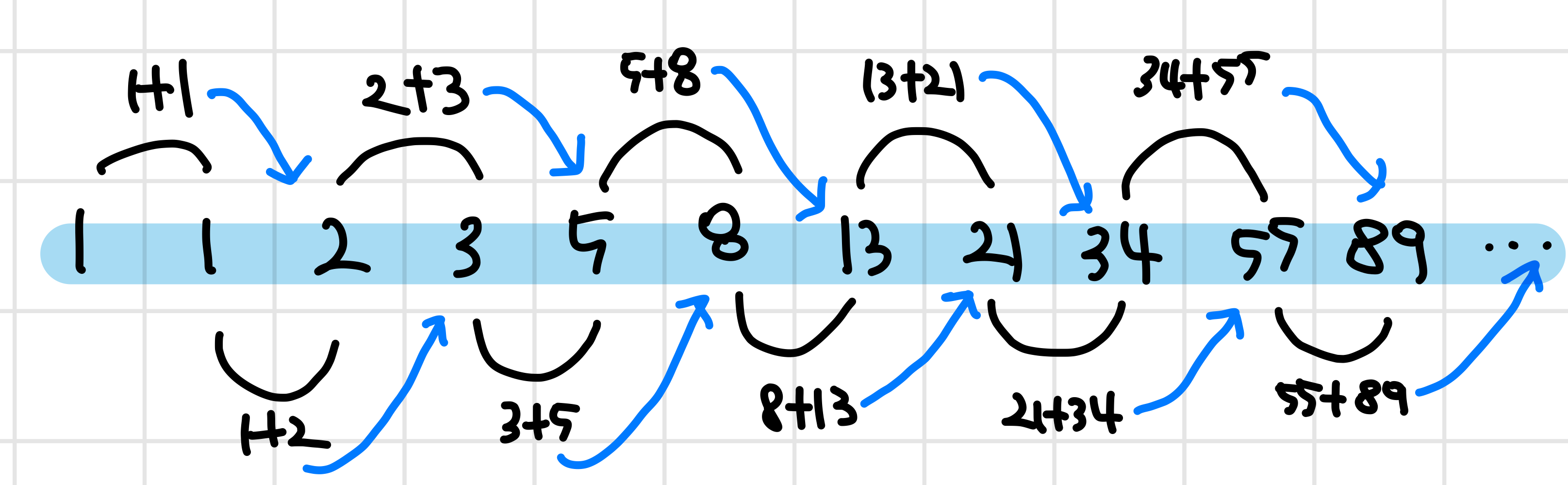
예시: 피보나치

• 피보나치는 1,1,2,3,5,8,13...의 수로 이루어짐 즉, n+2 수열 = n + 1 수열 + n의 수열
• n번째 피보나치 수 = (n-1)번째 피보나치 수 + (n-2)번째 피보나치 수
  단, 1번째 피보나치 수 = 1, 2번째 피보나치 수 = 1

재귀함수로 구현한 피보나치 함수

• 피보나치를 재귀함수로 풀게 될 경우 동일한 함수를 반복적으로 호출하게 되면서 수행 시간이 기하급수적으로 늘어남!
• 시간 복잡도: $O(2^n)$
  
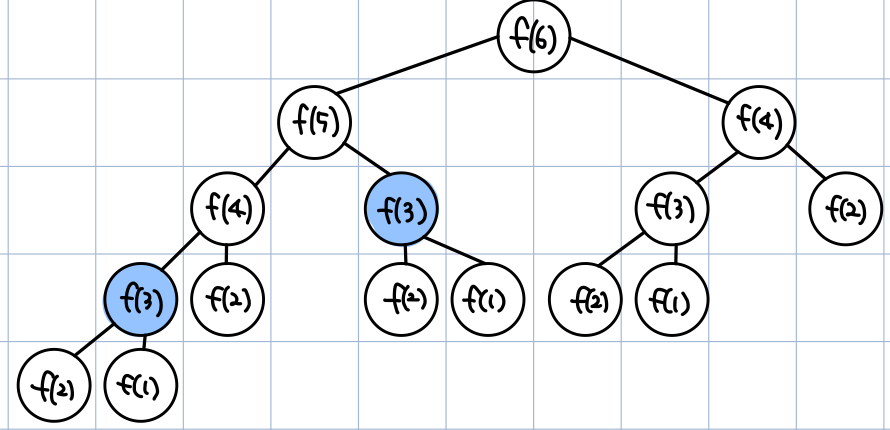
• f(6)의 호출과정을 그림으로 나타낸 것
• f(3)은 총 3번 호출 되었다. 즉, f(n)에서 n이 커지면 커질수록 반복해서 호출하는 수가 많아진다.

def fibo(x):
 	if x == 1 or x == 2:
    	return 1
    return fibo(x-1) + fibo(x-2)

print(fibo(4))

DP로 구현한 피보나치 함수

• 피보나치는 DP의 두가지 조건을 만족한다!
• 시간 복잡도: $O(n)$
• 그림처럼 색칠한 노드만 방문하면 됨, 점선으로 표현된 노드는 호출되지 않는다.
  

# 피보나치 함수를 재귀 함수로 구현 (탑 다운 DP)
# 한 번 계산된 결과를 메모이제이션하기 위한 리스트 초기화
d = [0] * 100
def fibo(x):
	# 종료 조건(1 혹은 2일 때 1을 반환)
 	if x == 1 or x == 2:
    	return 1
    # 이미 계산한 적 있는 문제라면 그대로 반환
    if d[x] != 0:
    	return d[x]
    # 아직 계산하지 않은 문제라면 점화식에 따라서 피보나치 결과 반환    
    d[x] = fibo(x-1) + fibo(x-2)
    retrun d[x]
print(fibo(99))

푸는 방식

• DP문제를 잘 해결하기 위해선 2가지
  1. 점화식을 세우는 것
  2. dp[i]에 도달하기 이전인 0 ~ i - 1 까지는 최적의 값이 저장되었다고 확신하는 것

탑다운(Top-Down) 방식

• 재귀함수를 이용하여 DP 소스코드를 작성하는 방법
• 큰 문제를 해결하기 위해 작은 문제를 호출하는 것

보텀업(Bottom-UP) 방식

• 단순히 반복문을 이용하여 소스코드를 작성하는 방법
• 작은 문제부터 차근차근 답을 도출하는 것
• 결과 저자용 리스트는 'DP테이블'이라고 부름

d = [0] * 100
# 첫 번째 피보나치 수와 두 번째 피보나치수는 1
d[1] = 1
d[2] = 1
n = 99

# 피보나치 함수 반복문으로 구현 (보텀업 DP)
for i in range(3, n+1):
	d[i] = d[i-1] + d[i-2]
print(d[n])