그리디 Greedy
눈 앞의 최적의 상황을 선택하여 최적의 해를 찾는 알고리즘
현재의 선택이 이후에 미칠 영향은 고려하지 않음
❗️그리디 알고리즘이 항상 최적의 해를 도출하지는 않음
그리디로 최적해가 보장되지 않는 경우
1. 이진 트리의 최적합 경로 찾기
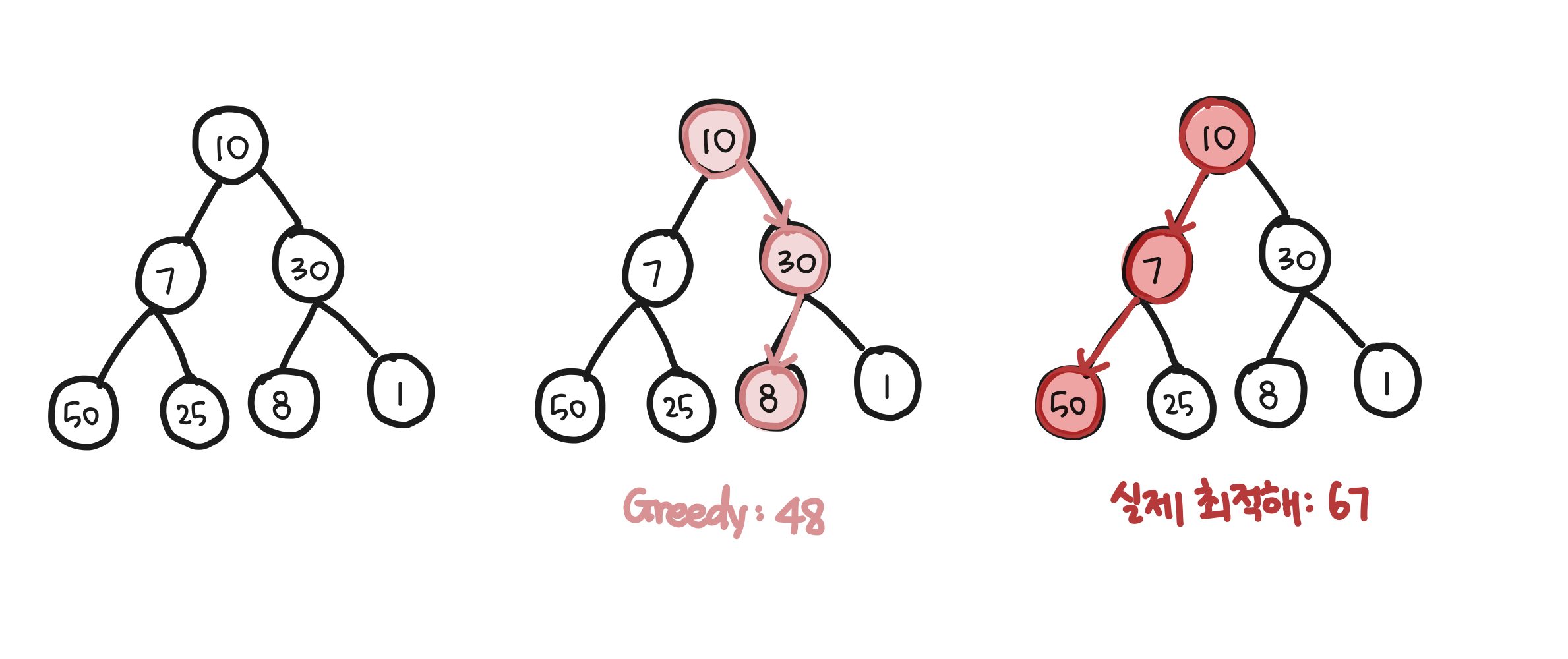
위와 같은 이진트리의 경우, 그리디로 값을 찾을 경우 최적합을 도출할 수 없다.
리프노드까지 방문을 해야 최적합을 알 수 있기 때문이다.
이 경우는 백트래킹으로 해결해야 한다.
유사한 문제 > 백준 - 1932 정수 삼각형
2. 보따리 문제
부피가 M인 보따리에 넣으려는 n개의 물건이 있다.
물건 i의 무게와 가치는 W(i), P(i)이다.
물건들의 전체 부피 합이 M을 넘지 않도록하고 물건들의 총 가치가 최대가 되도록 보따리에 넣는 문제.
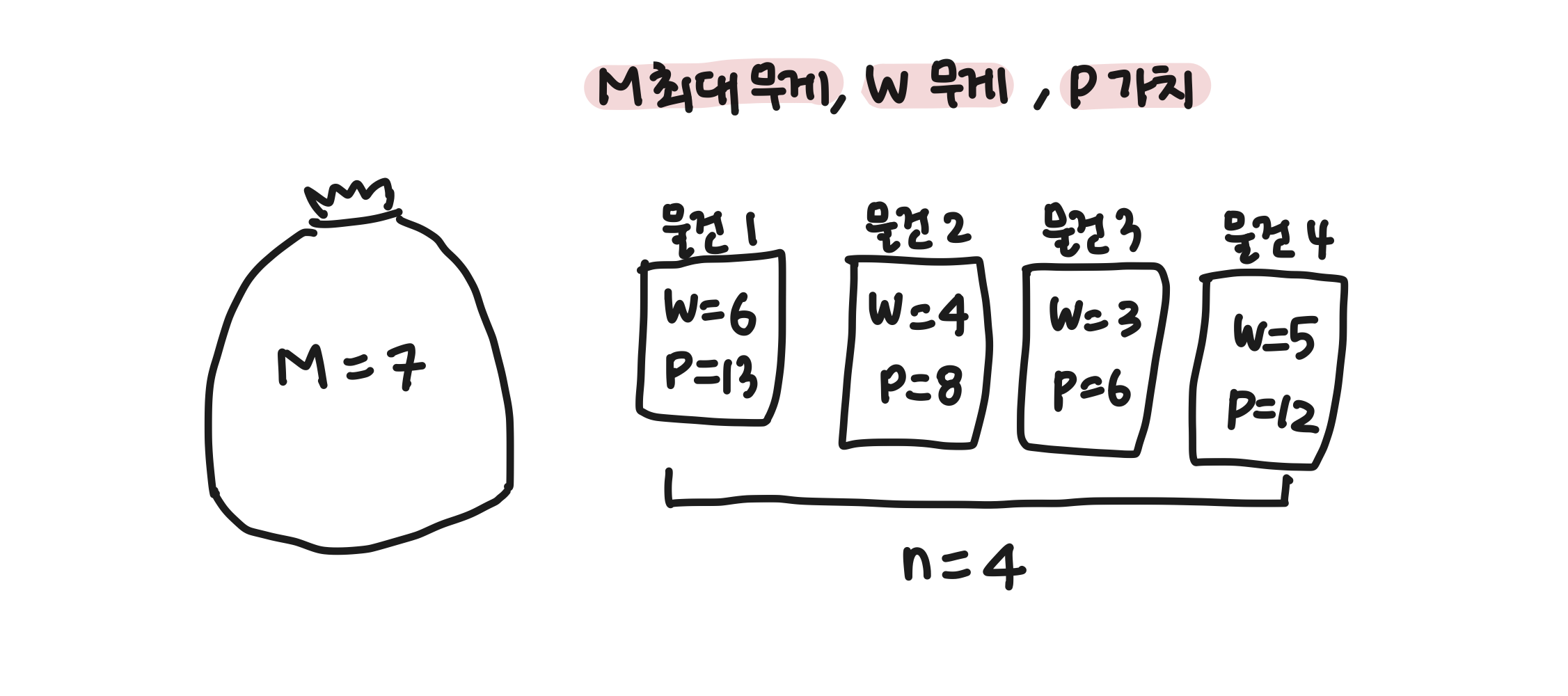
위와 같은 경우, 그리디로 구했을 때 물건 1을 골라 최대 가치 13을 도출하게 되지만, 실제 최적해는 물건 2와 3을 골라 최대 가치 14를 도출하게 된다.
이 경우는 dp로 해결해야 한다.
유사한 문제 > 백준 - 12865 평범한 배낭
(❗️하지만 만약 물건을 자를 수 있는 경우, 그리디로 해결할 수 있다. 이 유형의 문제를 자를 수 있는 보따리 문제라고 한다.)
3. 동전 바꾸기
가장 작은 동전을 사용해 n원을 만드는 문제.
동전의 종류가 [10, 50, 100, 500]인 경우 그리디로 최적해를 구할 수 있지만,
동전의 종류가 [10, 50, 75, 100, 400, 500]과 같은 경우 그리디로 최적해를 구할 수 없다.
다음 단위가 그 전 단위의 배수가 아니기 때문에 그리디로 최적해를 구할 수 없다.
예를 들어, 동전의 종류가 [10, 50, 75, 100, 400, 500]일때 1300원을 만들어보자.
그리디로 구할 경우 500원 * 2개 + 100원 * 3개 = 5개로 만든다.
그러나 실제 최적해는 500원 * 1개 + 400원 * 2개 = 3개로 만들 수 있다.
이 경우는 dp로 해결해야 한다.
유사한 문제 > 백준 - 2294 동전 2
그리디로 최적해가 보장되는 경우
1. 최소 신장 트리
그래프의 신장 트리 중 간선들의 가중치의 합이 가장 작은 신장 트리
-
프림 알고리즘은 한 점과 연결된 간선 중 가중치가 가장 작은 간선을 선택한다. 이는 그리디 알고리즘이다.
-
크루스칼 알고리즘은 간선의 가중치가 작은 순서대로 나열해놓고 순차적으로 선택한다. 이는 그리디 알고리즘이다.
유사한 문제 > 백준 - 1197 최소 스패닝 트리
2. 회의실 배정 문제
n개의 회의에 대해 시작시간과 종료시간이 주어진 경우, 가장 많은 수의 회의를 할 수 있도록 스케줄링하는 문제
회의 종료시간을 기준으로 오름차순 정렬하여 겹치지 않는 한에서 회의를 고르면 최적해를 구할 수 있다.
(❗️회의 시작시간을 기준으로 정렬하면 최적해를 고를 수 없다.)
유사한 문제 > 백준 - 1931 회의실 배정
3. 다익스트라 알고리즘
그래프의 가중치가 모두 0 이상인 경우에 특정 정점으로부터 최단 경로를 구하는 알고리즘
두 노드 사이의 거리가 최소인 경우를 선택한다. 이는 그리디 알고리즘이다.
유사한 문제 > 백준 - 1753 최단경로
