[그래프] 신장 트리와 최소 신장 트리(MST)

신장 트리 Spanning Tree

연결 그래프의 부분 그래프, 모든 정점과 간선의 부분 집합으로 구성

조건

1. 모든 정점이 연결되어 있어야 함

2. 간선의 개수 = 정점의 개수 - 1

3. 사이클이 없어야 함

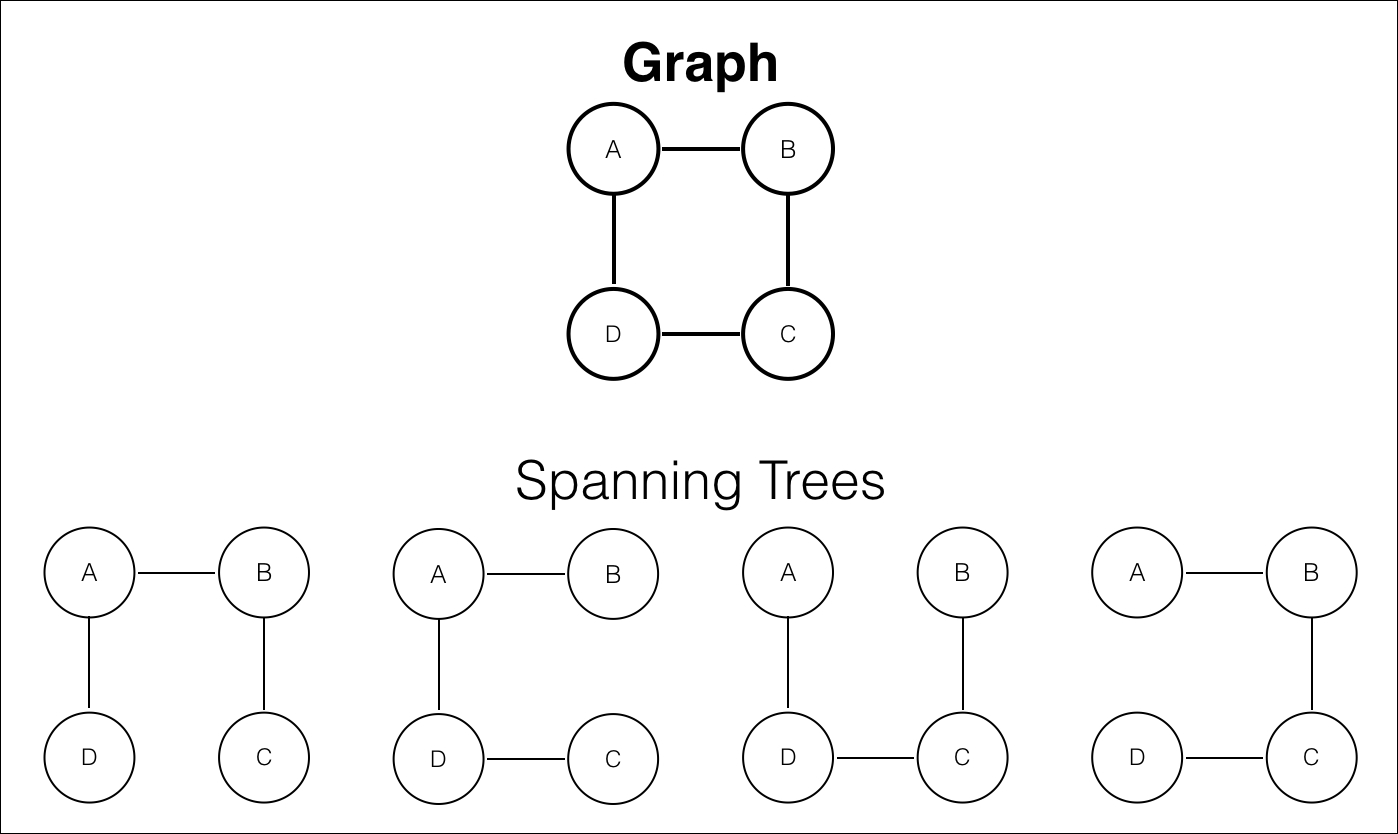
구현

dfs 혹은 bfs로 구현할 수 있음
-> 하나의 그래프는 여러개의 신장 트리를 가짐

---

최소 신장 트리 MST

Minimum Spanning Tree
그래프의 간선들의 가중치의 합이 가장 최소가 되는 신장 트리를 구성하는 것

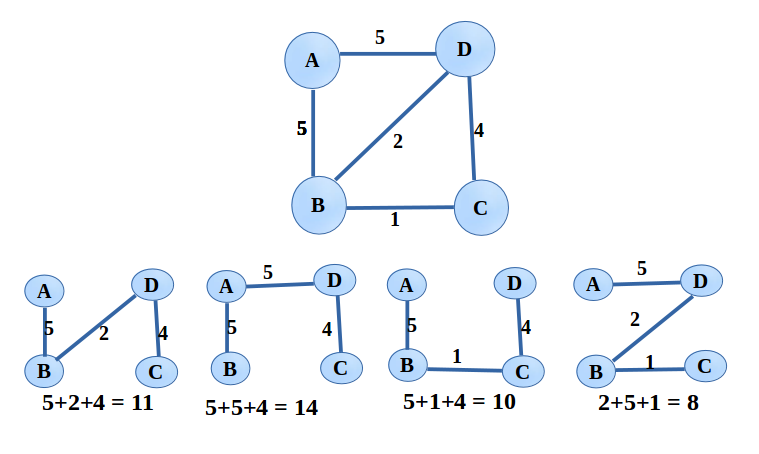
위 경우 가중치의 합이 8인 신장 트리가 MST이다

MST 알고리즘

1. 크루스칼 알고리즘 Kruskal’s algorithm

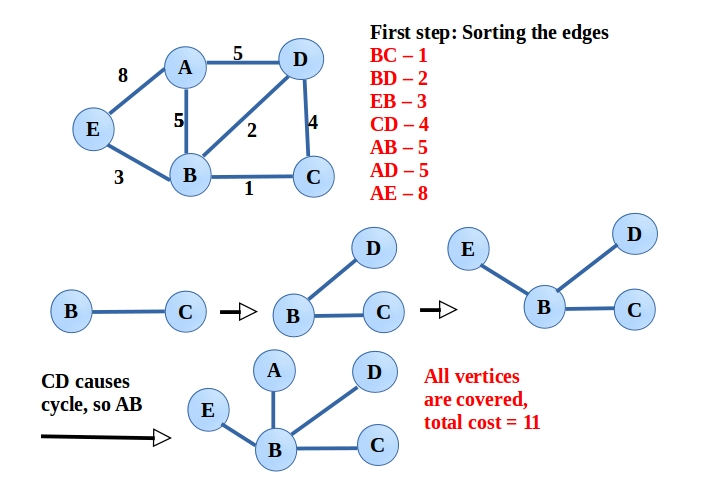
간선의 가중치를 기준으로 오름차순으로 정렬한 후, 정렬된 순서대로 간선을 선택한다(사이클이 생기지 않도록 선택).

2. 프림 알고리즘 Prim’s algorithm

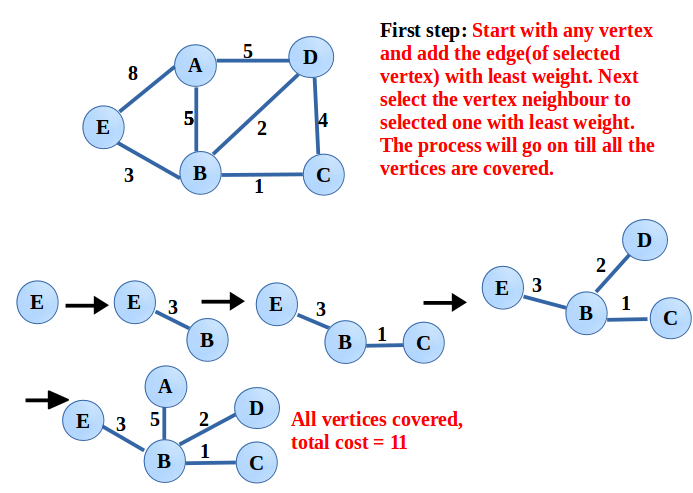
아무 정점에서부터 시작. 연결된 간선들 중 가중치가 가장 작은 간선을 선택한다(사이클이 생기지 않도록 선택).