[Pytorch Geometric Tutorial] 1. Introduction to Pytorch geometric

<References>

• Pytorch Geometric tutorial: Introduction to Pytorch geometric

Problems of dealing graph in deep learning

1. Different sizes
   • 노드 크기에 따라 adjacency matrix의 크기가 달라짐
2. NOT invariant to node ordering
   • 그래프가 위상적으로 동일하더라도 adjacency matrix는 다를 수 있음

Notation

Computation Graph

: The neighbour of a node define its computation graph

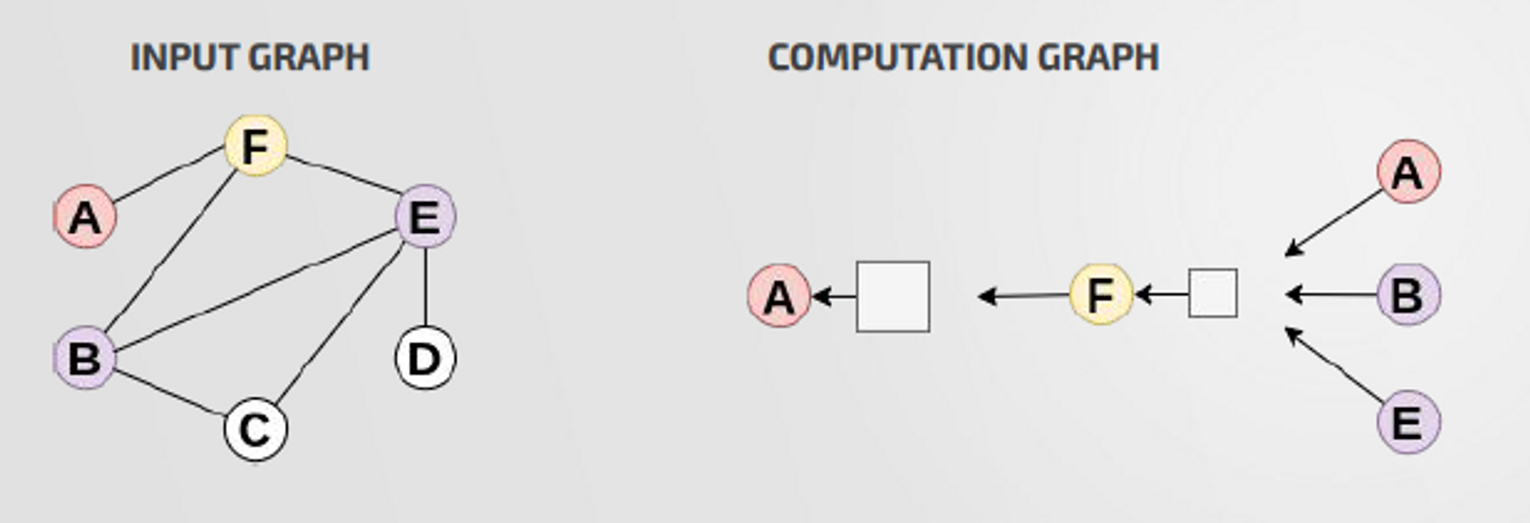
• Neighbor node들의 정보를 aggreagte하여 박스를 거쳐 target node의 representation을 만들어 냄
  • 박스 : Neural Network
  • Ordering invariant Aggregation : sum, average같이 노드 순서에 상관없는 노드 정보 aggregation
• redundancy : 각 노드들에 대해 2hop의 computational graph를 만들면 중복되는 부분이 발생하게됨

Math

1. 0번째 layer에서 node v의 representation은 node feature이다

• $H_v^0$ : layer0에서 노드 v의 representation
• $X_v$ : node $v$의 feature

1. 노드 representation update

• $h_v^{k+1}$ : layer k+1에서 노드 v의 representation
• $h_v^{k}$ : layer k에서 노드 v의 representation
• $\sum_{v \in N(u)} \frac{h_u^k}{|N(v)|}$ : 노드 v의 neighbor $N(v)$에 대해 임베딩을 평균한 것
• $W_k, B_k$ : Weights(박스), shared for all computation graph
• $\sigma$ : Activation function(relu)

1. k번째 layer에서 node v의 representation

GraphSAGE

Inductive Representation Learning on Large Graphs

위의 Math에서 간단한 수정으로 구현할 수 있음

• average ⇒ general aggregation function
• 주변 노드 정보를 합친 정보와 이전 layer의 자기 자신에 대한 정보를 더하는 대신, concatenate(,)

• $AGG$
  • Pool : Element-wise min/max
  • LSTM : note not order invariant

Implementations
https://github.com/sujinyun999/PytorchGeometricTutorial/blob/main/Tutorial1/Tutorial1.ipynb