[Pytorch Geometric Tutorial] 3. Graph attention networks (GAT) implementation

<References>

• Pytorch Geometric tutorial: Graph attention networks (GAT) implementation

💡 target node에 대한 neighbor node의 중요도가 모두 같지 않다

→ 특별히 더 중요한 노드가 있다고 할 때, 그 weight를 automatic하게 학습하는 방법?

⇒ GAT

Graph Attention Layer

• Input : set of node features $\mathbf{h} = \{\bar{h_1},\bar{h_2}, \dots ,\bar{h_n}\} \quad \bar{h_i} \in \mathbf{R}^F$
• Output : a new set of node features $\mathbf{h'} = \{\bar{h'_1},\bar{h'_2}, \dots ,\bar{h'_n}\} \quad \bar{h'_i} \in \mathbf{R}^{F'}$

1. apply a parameterized linear transformation to every node

• $(F' \times F) \cdot F$ matrix연산 ⇒ $F'$

2. Self attention

• $e_{i,j}$ : Specify the importance of node j’s features to node i

3. Normalization

4. attention mechanism $a$ : a single-layer feed forward neural network

• 주변노드 j의 임베딩과 자기 자신노드 i의 임베딩을 각각 parameter update한 후 concatenate
• LeakyReLU

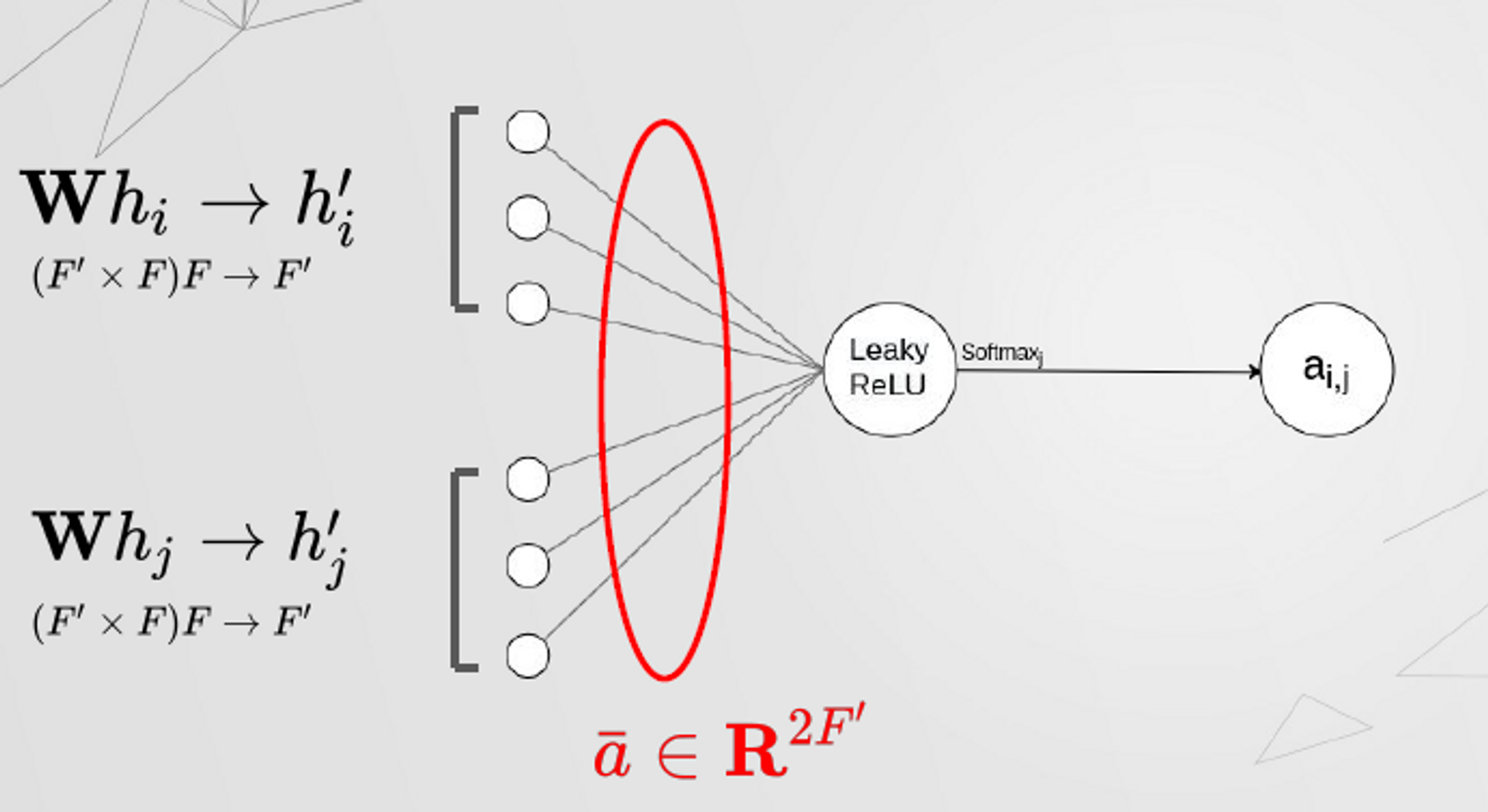
• $||$ : concatenate → $F' + F'$
• $[\mathbf{W}h_i||\mathbf{W}h_j]$ → $(2F' \times 1)$
• $a^{-T}$ : transpose(a) → $(1\times 2F')$
• LeakyReLU(Real number)

5. 학습한 attention 사용하기 : Node i의 이웃의 중요도를 결정하여 Input 데이터를 재정의

6. Multi-head attention($K$번 반복)

   1. Concatenation : in layer

      $h'_i = ||_{k=1}^K\sigma(\sum_{j\in N(i)} \alpha_{i,j}^k \mathbf{W}^kh_j)$

   2. Average : on the final prediction layer of the network

      $h'_i = \sigma(\frac{1}{K}\sum_{k=1}^K \sum_{j\in N(i)} \alpha_{i,j}^k \mathbf{W}^kh_j)$

👍Advantages

• Computationally efficient
  • Self-attention layers can be parallelized across edges
  • Output features can be parallelized across nodes
• Allows to assign different importances to nodes of a same neighborhood
• It is applied in a shared manner to all edges in the graph
  • Not required to have the entire graph
• Works in both
  • Transductive learning (Cora, Citeseer, Pubmed) : Big whole graph에 접근하여 node classification을 하거나 link prediction
  • Inductive learning (PPI) : Multiple graphs, 다른 그래프셋에 대한 예측

Message Passing Implementation

Creating Message Passing Networks - pytorch_geometric documentation

torch_geometric.nn.conv.message_passing - pytorch_geometric documentation

• 자기자신, 주변 노드들, 엣지 정보를 concat하여 message를 만들고, 이를 aggregate하여 자기자긴노드와 한번 더 합친 뒤, 한번 더 MLP에 먹여주면 업데이트된 노드 임베딩
• $\mathbf{x}_i^{(k)}$ : Features representations of node i at the k-th layer (업데이트 하고싶은 것)
• $\phi^{(k)}$ : Differentiable function, Eg. MLP
• $\mathbf{x}_i^{(k-1)}$ : Feature representation of node i at the (k-1)-th layer
• $*\mathbf{x}_j^{(k-1)}$* : Feature representation of node j at the (k-1)-th layer
• $*\mathbf{e}_{j,i}$* : [optionally] features of edge (i,j)
• $f_{j\in N(i)}$ : Differentiable, ordering invariant function. Aggregate function. For every j in the neighbourhood of i. Eg. sum, average, etc...
• $\gamma^{(k)}$ : Differentiable function, Eg. MLP

PyTorch Geometric MessagePassing base class

PyTorch Geometric 탐구 일기 - Message Passing Scheme (1)

• GNN의 MessagePassing Shceme에 대해, propagation을 구조적으로 연결해주는 편리한 클래스
• message(), update(), aggregation를 설정
• $\phi^{(k)}$ : message()
• $\gamma^{(k)}$ : update()
• $f_{j\in N(i)}$ : aggregation → max, mean, add,,,
• flow : flow direction of message passing : 주변 노드로부터 정보를 전달 받을지, 전달할지 결정 (either "source_to_target" or "target_to_source")
• node_dim : 노드의 차원을 의미
  • defualt 값은 int 0
  • 어떤 axis로 propagate할지 결정하는 것

ex. Message Passing interface 예시

class MyOwnConv(MessagePassing):
    def __init__(self):
        super(MyOwnConv, self).__init__(aggr='add') # add, mean or max aggregation
        
    def forward(self, x, edge_index, e):
        return self.propagate(edge_index, x=x, e=e) # pass everything needed for propagation
    
    def message(self, x_j, x_i, e): # Node features get automatically mapped to source(_j) and target(_i) nodes
        return x_j * e

• torch.nn.Module이 superclass
• torch.nn.Module ⇒ torch_geometric.nn.MessagePassing ⇒ OurCustomLayer
• 대부분의 torch_geometric.nn.conv layer 구현체들이 Message Passing Scheme을 따름

MessagePassing - propagate()

def propagate():
   	if mp_type == 'adj_t' and self.fuse and not self.__explain__:
          	out = self.message_and_aggregate(edge_index, **msg_aggr_kwargs)
         
      # Otherwise, run both functions in separation.
       elif mp_type == 'edge_index' or not self.fuse or self.__explain__:
           msg_kwargs = self.__distribute__(self.inspector.params['message'],
                                             coll_dict)
           out = self.message(**msg_kwargs)
           out = self.aggregate(out, **aggr_kwargs)
  	out = self.update(out, **update_kwargs)

• propagate(edge_index, size=None, **kwargs)
• node embedding을 업데이트하고 message를 구성하기 위한 edge index등 다양한 추가 정보를 가져옴
• size → bipartite graph처럼 (N,M) 사이즈도 propagate 가능
  • 이 경우, size = (N,M) 으로 넣어줌
  • size = None 일경우 정사각행렬
• message()와 update() 함수를 차례로 호출
• message와 aggregate 함수는 분리되거나 합쳐져 사용
• 최종적으로 update 함수를 통해 출력값 생성

MessagePassing - message()

def message(self, x_j: torch.Tensor) -> torch.Tensor:
    # need to construct
    return x_j

• $\phi$, 노드 i에 대한 message구성
• message(**kwargs)
  • 각 edge마다 발생하는 “message”라는 것을 어떻게 construct할지 구체화하는 함수
  • propagate의 호출을 따르므로, propagate에 전달할 어떤 인자든 넘길 수 있음
  • 주의할 점, 메세지 간의 노드를 구체화할 때는, “_i”와 “_j”를 구분해서 표현해야 mapping이 정의 가능
    • i : central node
    • j : neighboring nodes
    • flow=’sourceto_target’일 경우, $e{ij}\in E$ 로 구분
    • flow=’targetto_source’일 경우, $e{ji}\in E$ 로 구분
• 따라서, 함수의 argument naming이 중요

MessagePassing - update()

def update(self, inputs: torch.Tensor):
    # need to construct
    return inputs

• $\gamma$, 각 노드 i에 대해서, node embedding을 업데이트하는 함수
• update(aggr_out, **kwargs)
  • message의 aggregation 결과값을 inputs 인자로
  • 처음 propagate()에 전달한 초기 인자들도 이용 가능

Implementing the GCN Layer

Semi-Supervised Classification with Graph Convolutional Networks

• 이웃 노드들의 feature들이 weight matrix $\mathbf{W}$로 먼저 transform되고, node degree들로 normalize됨
• bias vector $\mathbf{b}$를 적용해 output을 aggregate
• Comparison with general message passing
  • $\mathbf{x}_i^{(k)} = \gamma^{(k)}(\mathbf{x}_i^{(k-1)},f_{j\in N(i)}\phi^{(k)}(\mathbf{x}_i^{(k-1)},\mathbf{x}_j^{(k-1)},\mathbf{e}_{j,i}))$
  • $\sum_{j \in \mathcal{N}(i) \cup \{ i \}} \frac{1}{\sqrt{\deg(i)} \cdot \sqrt{\deg(j)}}$ = $f_{j\in N(i)}$
  • $\mathbf{W}$ = $\phi^{(k)}$

Steps

1. Add self-loops to the adjacency matrix.(본인 노드 feature도 넣어줌, 대각 성분을 1로)
2. Linearly transform node feature matrix.
3. Compute normalization coefficients.
4. Normalize node features in $\phi$
5. Sum up neighboring node features ("add" aggregation).
6. Apply a final bias vector.

• Step 1~3 : sum 기호 내부, 타겟 노드에 전달해줄, 흐르게 할 (propagating할) message를 construct하는 과정
• Step 4~6 : 이웃인 node-pair에 대해 aggregation하고 해당 타겟 노드를 update하는 과정

Source Code

import torch
from torch.nn import Linear, Parameter
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops, degree

class GCNConv(MessagePassing):
    def __init__(self, in_channels, out_channels):
        super().__init__(aggr='add')  # "Add" aggregation (Step 5).
        self.lin = Linear(in_channels, out_channels, bias=False)
        self.bias = Parameter(torch.Tensor(out_channels))

        self.reset_parameters()

    def reset_parameters(self):
        self.lin.reset_parameters()
        self.bias.data.zero_()

    def forward(self, x, edge_index):
        # x has shape [N, in_channels]
        # edge_index has shape [2, E]

        # Step 1: Add self-loops to the adjacency matrix.
        edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))

        # Step 2: Linearly transform node feature matrix.
        x = self.lin(x)

        # Step 3: Compute normalization.
        row, col = edge_index #출발, 도착 노드 분리
				#도착노드에 대해 node 등장횟수 count
        deg = degree(col, x.size(0), dtype=x.dtype)
        deg_inv_sqrt = deg.pow(-0.5)
        deg_inv_sqrt[deg_inv_sqrt == float('inf')] = 0
        norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]

        # Step 4-5: Start propagating messages.
        out = self.propagate(edge_index, x=x, norm=norm)

        # Step 6: Apply a final bias vector.
        out += self.bias

        return out

    def message(self, x_j, norm):
        # x_j has shape [E, out_channels]

        # Step 4: Normalize node features.
        return norm.view(-1, 1) * x_j

GCNConv

• “add” propagation을 사용한 MessagePassing을 상속받음

• foward()

  • Step 1: Add self-loops to the adjacency matrix → [torch_geometric.utils.add_self_loops()] : https://pytorch-geometric.readthedocs.io/en/latest/modules/utils.html#torch_geometric.utils.add_self_loops
  • Step 2: Linearly transform node feature matrix → [torch.nn.Linear] : https://pytorch.org/docs/master/generated/torch.nn.Linear.html#torch.nn.Linear
  • Step 3: Compute normalization → $1/(\sqrt{\deg(i)} \cdot \sqrt{\deg(j)})$ → [num_edges, ] 크기의 tensor norm output
    • torch_geometric.utils.degree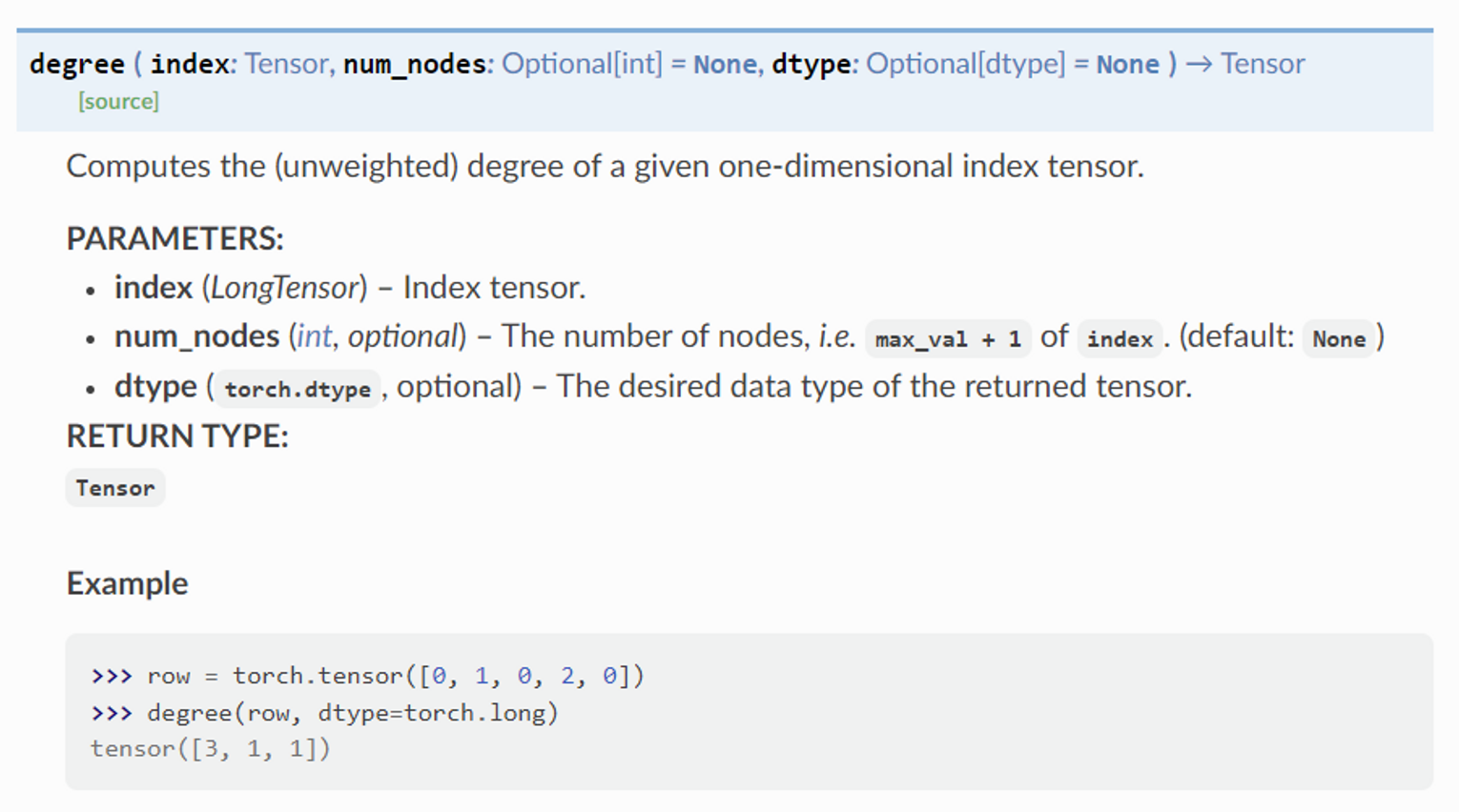
  • Step 4-5: Start propagating messages. → call propagate() → 내부적으로 message(), aggregate(), update()
    • propagate() : node embedding을 업데이트하고 message를 구성하기 위한 edge index등 다양한 추가 정보를 가져옴
      • node embeddings x, the normalization coefficients norm 를 추가 전달
  • Step 6: Apply a final bias vector.

• message()

  • normalize the neighboring node features x_j by norm
    • x_j : lifted tensor, 각 엣지의 source node feature를 포함
    • x_i : 각 엣지의 target node feature를 포함
    • i : central node
    • j : neighboring nodes

Implementations
https://github.com/sujinyun999/PytorchGeometricTutorial/blob/main/Tutorial3/Tutorial3.ipynb